0) 69.098.6:624.971.2 cust. 28 ube Design of shear wall buildings FITTITTITTT. REPORT 102REPORT 102 Design of shear wall buildings AW. IRWIN PhD BSc(Eng) CEng MiStructE MICE. Price: £50 (£10 CIRIA Members after free allocation) ISBN: 0 86017 215 5 ISSN: 0305 — 408% ©CIRIA 1984 CONSTRUCTION INDUSTRY RESEARCH AND INFORMATION ASSOCIATION SSTOREY'S GATE, LONDON SW1P 3AU ‘Telaphone 01-222 8801 Telex 24224, Mono Ret. prefix 2063 \Foreword ‘The Project culminating in this Report was carried out by Dr A.W. Irwin of Heriot-Watt University. ‘The work was guided by a Project Steering Group comprising: Mr S.J. Alexander Kenchington, Little & Partners Professor A. Coull University of Glasgow Dr AR. Jeary Building Research Establishment Dr D, Michael Ove Arup & Partners Mr G. Pinfold NCL Consulting Engineers DrNK.Subedi University of Dundee (Formerly Taylor Woodrow Research Laboratory) ‘The Project was partly funded by the Property Services Agency. ‘This Report was prepared for publication by Dr R.M. Lawson, CIRIA Research Manager for Structural Design ‘The purpose of this Report isto collect together and present information for structural designers on tall buildings of shear wall form, The divergence between design practice and the complexity of ‘many research papers in the fields which influence the structural design is apparent. The Report endeavours to simplify these analytical techniques while retaining their potentially attractive features, Although every attempt is made to offer positive design guidance, there isa lack of information on the behaviour of real structures with which to appraise these proposals. It is hoped that with subsequent use, the guidance will be in improved in certain fields. Feedback on the usefulness or limitations of this information, and on the performance of tall buildings in service would be welcomed by CIRIA, Much of the infomation used has been obtained from international sources, such as the American Society of Civil Engineers and the New Zealand Society for Earthquake Engineering, whose contribu tions are gatefully acknowledged CIRIA Report 102Contents CIRIA Report 102 LIST OF ILLUSTRATIONS...... LIST OF TABLES. . NOTATION . SUMMARY........-. INTRODUCTION _ 1, DESIGN CONSIDERATIONS. 11 12 1.3. Reinforced concrete design of walls . 1.4 — Fire design, 1.5 Foundation design. 1.6 Constructional features . 2. CATEGORIES OF LIMIT STATE 2.1 Ultimate limit state... 2.2 Serviceability limit state . .. 2.3. Survival limit state. . 3. ELASTIC DESIGN OF SHEAR AND CORE WALLS. 3.1. Design of slender walls in compression . . . 3.2 Design of walls under axial load and moment . 3.3 Elastic analysis of pierced shear walls 3.4 Structural interaction of shear walls . 3.5 Computer modelling of shear walls 3.6 Elastic analysis of core walls ....... 4. DYNAMIC ANALYSIS OF SHEAR WALL BUILDINGS........... 4.1 Approximate calculation of natural frequency . 4.2 Dynamic response of shear walls . 43 Wind loading on 95 44 Human response to motion... . 5. ELASTO-PLASTIC AND SEISMIC BEHAVIOUR . 5.1 Ultimate strength of walls in compression and bending 5.2 Approximate elasto-plastic analysis of pierced shear walls. 5.3 Seismic design methods. 5.4 Design and detailing for elasto-plastic behaviour... STRUCTURAL VARIATIONS. 6.1 Behaviour of panel structures .... 6.2 Behaviour of infill panels to frames. . 7. DESIGN CONCLUSIONS. .. REFERENCES. APPENDIX 2 Formulae for pierced shear walls .......-..List of illustrations Figure 31 Figure 32 Forms of shear wall structure Different plan configuration of shear and core walls Piled-raft foundation for shear wall Possible wall failure modes Forces developed as a result of panel removal Design of reinforced concrete walls in compression Equilibrium of channel section wails in elastic and plastic ranges Maximum elastic force on flange of channel sections, under moment and axial force Maximum elastic force on wall with single outstand, under moment and axial force Forces in lintel beams Different shear force distribution, depending on degree of coupling Design chart for lintel forces for uniform lateral loading Design chart for lintel forces for triangular lateral load distribution Relative properties of various wall geometries Relative deflection of coupled walls Effective slab widths for various cases Analysis of plan behaviour of shear wall building Load sharing between elements of nominally similar stiffness Variation in centre of rotation of typical building Mode! of shear wall by discrete line elements Representation of complete building by line elements Computer model of shear wall building Behaviour of core walls in bending Behaviour of two forms of core walls in torsion Geometry of core with channel walls Lumped mass representation of coupled shear wall Effect of torsional properties on natural frequency of building Wind forces on rectangular building Wind turbulence parameters for dynamic analysis Design chart for broad-band wind response Curves of perception and satisfactory magnitudes of horizontal structural motion with respect to human response Ultimate moment-axial force curves for plane and channel walls Example of ultimate strength analysis of reinforced concrete wall Elasto plastic forces in lintels of pierced shear wall Plastic deformation of lintel Approximate elasto-plastic behaviour of typical pierced shear wall Behaviour of shear wall up to failure ‘Shear behaviour of low-rise wall Design response spectra for seismic loading Reinforcement in ductile coupling beams under repeated cyclic deformation Effective section of wall in elasto-plastic action Detailing requirements for potential yield zones Shear displacement relationships for forms of construction joint Simplified arrangement of reinforcement in shear wall Different forms of joint reinforcement Joint types used in panel construction Typical shear-displacement curves for various joints Typical load-deflection curve for a steel frame with infill Idealised plastic failure modes for infill frames Representation of frame and infill for analysis Typical shear wall building used for design calculation CIRIA Report 102List of tables Limiting height of buildings, above which they are treated as high rise for fire design ‘Minimum thicknesses of walls for various fire ratings Load factors specified by various codes Approximate methods of estimating the natural frequencies of buildings Calculation of natural frequencies of building on Figure 19 ‘Dynamic properties of various high-rise buildings ‘Damping ratios for various stress levels Approximate ratios of gust to mean wind speeds for different averaging perio Approximate description of earthquake intensities ‘Suggested approach to design of shear wall buildingsNotation cross-sectional area of wall total area of reinforcement in wall length of coupling beam (lintel) ‘outstand length of flanged wall force coefficient for wind on building face depth of coupling beam overall depth of building eccentricity of load on wall =M/N) eccentricity of load used in column analysis, eccentricity of plan centre of mass of building from centre of rotation excitation frequency cube strength of concrete frequency of nth mode of vibration yield strength of steel natural frequency of building in z plan direction ‘gravitational acceleration ratio of extreme wind speed to root-mean-square value, Oy oF 05 model participation factor used in dynamic analysis wall height between floors effective height of wall height of shear wall inertia of coupling beam (lintel) effective inertia of coupling beam inertia of uncracked section in-plane inertia of walls ‘effective stiffness of wall distance between centroids of wall sections length of planar wall or web of flanged wall modular ratio between steel and concrete lumped mass of element, in-plane moment on wall applied in-plane moment on wall, ultimate in-plane moment of wall in presence of axial load, ultimate moment of resistance of lintel (coupling beam) axial force on wall ultimate strength of unit length of concrete wall in compression number of storeys of height, h ‘maximum elastic force on unit length of wall in presence of axial load and moment tensile strength of reinforcement (= 0.87 fyAs) compressive strength of reinforcement (=0.73 fy) ultimate compressive strength of wall ratio of area of tensile reinforcement to cross-sectional area of coupling beam (lintel) lateral load at point x; on wall shear force in coupling beams (lintels) ultimate shear force in coupling beams base shear force from wind action ratio of area of tensile reinforcement to cross-sectional area of wall radius of gyration of building mass about the centre of rotation response spectrum ordinate distance of shear-entre of channel from web factor in determining seismic forces on building thickness of wall axial force in wall resulting from coupling action timescale of wind gusts displacement of wall lateral displacement of wall 04 feat) CARLA Report 102wee Nee > sgseen ae ‘mean wind speed at height, #7 wind speed averaged over period, ¢ 34s gust wind speed in-plane lateral loading on wall angular frequency of mode n of building vertical co-ordinate of point on wall position of neutral axis from compression face as determined by elastic analysis of wall, height position of lateral load, Position of maximum coupling beam (lintel) deformation in plastic analysis limits of plastic zones of lintel deformation plan dimension transverse to applied loading plan centre of rotation from reference point plan dimension in direction of applied loading ground roughness structural admittance used in dynamic analysis fexponent in wind analysis (Section 4 only) parameter in determining stiffness of pierced shear walls relative stiffness parameter used in analysis of pierced shear walls parameters in torsional analysis of core damping ratio rotation of lintels mode shape rotation of lintels corresponding to onset of yield shear coefficient for concrete in-plane rotation of floor root mean square — broad-band response for wind analysis root mean square ~ narrow-band response for wind analysisSummary ‘The design of shear and core walls is reviewed. This is based on available methods of analysis, covering their elastic, elasto-plastic and dynamic behaviour. The various limit states of design are put forward, and the importance of serviceability criteria (c.g. the response of the occupants of the building to motion) are described. The Report concentrates on the design of coupled shear and core walls, but it also examines structural variations such as panels and inflls. A suggested design procedure is Gescribed, and typical design calculations are presented. Introduction ‘The purpose of this Report sto present guidance on the design of tall buildings (height $0 to 100m)of shear wall form. Such structures, which are designed to resist lateral loads by’planar wall gr core elements, are not specifically considered by codes of practice for reinforced concrete?) The guidance is expressed in limit-state terms both with regard to strength under various loading conditions, and to the requirements for satisfactory performance in service, Research into the analysis of tall buildings has been extensive ?, but a large proportion is not easily used in design. The objective of this study was to distill this research into a rational design process. It was not intended to dictate precise positioning, shape, detailing, and methods of con- Strueting shear-wal building, but merely to present information and methods upon which design decisions may be base: Shear walls offer a structurally efficient means of enclosing and utilising space. Their stiffness is such that sway movement under wind load can be minimised. ‘There are a number of generic forms of shear wall structure. The ability to analyse their behaviour accurately is often limited, and conservative approximations are justified. When exposed to pre- dominantly static loading, such monolithic walls (with or without openings) may generally be designed by elastic methods. However, in seismic design, the controlling criterion is often energy absorption by plastic deformation. ‘The following sections describe the various force and dynamic actions which need to be considered, the relevant limit states of design with their methods of analysis, and the variations in form of shear wall buildings. A suggested design process for evaluation of both force actions and structural responses is put forward in the design conclusions (Table 10, page 68). Scheme design calculations for a typical shear wall building are presented in Appendix 1 CIRIA Report 1021. Design considerations 1.2.1 Applied loads CIRIA Report 102 1.1 TALL BUILDING STRUCTURAL FORMS ‘A change in structural design from moment-tesisting frames to flexible frames with stiff shear resisting clements has occurred in recent years. Shear wall buildings are commonly of 10 to 30 storeys, and their behaviour is influenced by the shape of the walls and their plan position, Monolithic shear walls can be classified as short, squat or cantilever (see Figure 1) according to their height/depth ratio, The walls may be planar, flanged or core in shape. In many cases, the walls are pierced by openings such that the behaviour of the individual wall sections is coupled to a variable degree, depending on the proportions of the walls and connecting beams. In their simplest form, a single line of openings may be respresented for analysis as a continuous flexible medium, Shear cores usually comprise channel sections coupled by beams or slabs. ‘The plan distribution of walls should be such that the building is torsionally, as well as flexurally, stiff (Figure 2), In rectangular plan buildings, shear walls are often placed at the extremities of the building in order to resist load on the wider face of the building, In the orthogonal direction, frame action may be utilised. Wind resisting cores (rather than pierced shear walls) are usually preferred internally within buildings. Office buildings often comprise a single central service core surrounded by a ‘flexible’ frame. Many structures are made of load-bearing panels or shear infill. Their behaviour is affected by the Interaction between the elements a8 well asthe overall tructual action of the shear wall, The design of such structures has been reviewed by Fintel ‘) and CIRIA Report 45¢*), and it is summarised in Section 6. The main emphasis of this Report is on the design of coupled shear and core structures, including their elastic, elasto-plastic and dynamic behaviour. Other tall structural forms (such as the ‘frame- tube’ concept, podium floors, and hanging structures) are not specifically considered here. 1.2 FORCE ACTIONS In limit¢tate design, forces are multiplied by theis appropriate load factors to equate to the structural strength), The load factors are related to the levels of probability of loading and to possible combinations of load (see Section 2.1, page 15). Accurate assessment of loading is often difficult, particularly when such events are infrequent Force actions can be categorised as applied loads, environmental actions, and movement-related effects. Not only must the structure be able to resist the factored loading adequately, but it must perform satisfactorily under smaller, but more frequent, cycles of loading. Dead load Structural and dead weight is important because it contributes to overturning resistance of the foundations. Certain shear wall clements receive relatively little vertical load in comparison to the lateral load which they are required to resist. Estimation of dead weight is often difficult, Serious under estimates, particularly where there is heavy plant or cladding, can lead to increased dynamic response. Imposed load The intensities of prescribed floor loading depend on the use of the building. The CIRIA/BRE and other studies of office loading'”*) showed that much smaller loads act ove a wide flor area compared to the design loading on a single element. CP3) permits a reduction in the average loading per floor when designing a vestical member, depending on the number of storeys above it. For ‘buildings of more than 10 storeys, the average loading on the wall reduces to 50% of the prescribed loading. This is not applicable where there are loads from storage, or heavy plant material, All floors ‘may be considered to be uniformly loaded in assessing overall structural action. Vibration and blast loading In severe cases of vibration-induced forces resulting from traffic or machinery, vibration isolation ‘mountings can be used to advantage. However, such mountings may increase the fundamental period of the structuze as well as its damping, The damage from blast loading caused by gas explosions etc. came to prominence after the Ronan Point Collapse in 1969. The Building Regulations were subsequently amended "®) to require an element to resist a notional lateral pressure with a reduced safety factor, or to develop alternative toad paths for the structure with that element removed (see Section 2.3, page 17).Figure 1 Forms of shear wall structure Shear Bending Bending and shear a > Short Cantilever (a) Shape of shear walls Single row Two rows (b) Forms of openings in shear walls Plane Flanged Forms of channel f-—— Walls ——» +—__—Cores —__-» (c) Shape of shear and core walls CIRIA Report 102Figure 2 Different plan configuration of shear and core walls CCIRIA Report 102 (i) Walls resist bending in one plane. Frame action in other plane. Good torsional stiffness. \| 1 oo .» a@ iH (ii) Walls cesist bending in both planes. r Good torsional stiffness. a a {iii) Core resists bending in both planes. Poor torsional behaviour due to eccentricity. (iv) Cores resist bending in both planes. Good torsional stiffness. (¥) Cores resist bending on each section of the building independently. Relative shear displacement at movement joint1.2.2. Environmental effects 1.2.3. Movement effects 12 Wind loading Lateral loading often dictates the proportions of a shear wall building. Wind loading is characterised by a design wind speed at a certain recurrence period, In the design of buildings, a l-in-5O-year recurrence wind is used to assess the ultimate strength of the structure, Including the load factor for wind, this is equivalent to a limiting strength condition under an extreme wind speed of recurrence about 1 in $00 years. Both the steady and the gust components of the wind contribute to the structural response (see Section 4.3, page 42). The increase in load over that of the building considered quasi-statically (ce. as a rigid structure) is termed the ‘dynamic magnification of load’. In inner city areas, the dynamic component of load may be enhanced by buffeting of the wind between buildings, although the total loading is less than that for exposed sites. The occupants of the building may also perceive dynamic motion induced by wind. Local cladding pressures (particularly suction at the comers of the building) can be considerably higher than those used in ‘caloulating the overall loads on the building. Wind flow at ground level around buildings can also be an important environmental factor, and some means of dissipating local gusts may need to be investigated, ‘Seismic loading In many parts of the world, ground accelerations from seismic activity can be the principal design condition (see Section 5.3, page $5). This is usually expressed in terms of an equivalent lateral loading (S to 20% of total vertical load is typical). In more severe cases, the structure should be able to absorb the energy of the carthquake by elasto-plastic loading cycles. This imposes a need for careful detailing of the structure. Creep and shrinkage of concrete ‘These effects take place over a number of years, and they may be estimated using References 11 and 12, Both are a function of the environmental conditions, construction sequence, size of members and concrete mix proportions. Creep of concrete is strongly affected by the age at loading. Relative vertical movements between clements with different properties, or which are differentially loaded, can be significant. ‘This is important where brick infills may be used within a reinforced concrete frame (see Section 6.2, page 65). Similarly, differential movement between a reinforced concrete core and a steel frame ‘may be 2 to 3 mm per storey height. Because of the construction sequence, differential movement between a slip-formed concrete core and concrete frame may also be significant. In buildings of more than 60 to 70 m length, movement joints are normally provided to reduce the out-of-plane deformation of the walls resulting from differential horizontal movement between the floors and the roof. The positioning of movement joints as shown in Figure 2 (page 11) also influences the overall structural action of shear wall buildings Temperature Differential temperature movement between the roof and internal floors and the basement, or between exposed and shaded sides of the building or exposed and insulated members can be significant, and it may need to be considered as for creep and shrinkage, Relative movement between clements such as mullions and windows should be taken into account in detailing of the joints, Outof plumb walls Because of sway displacements, construction tolerances, and differential settlement, the enhanced, ‘moment resulting from axial loading (P-5 effect) should be taken into account in design. Control of verticality should be maintained during construction by precise optical plumbing methods. 1.3 REINFORCED CONCRETE DESIGN OF WALLS Walls are usually designed as compression elements under the combined action of in-plane bending and axial forces ). Lateral restraints ate required at each floor level, and adequate tie reinforcement should be provided. The wall should be braced against relative translation of its ends. The compres- sive resistance of a wall element is a function of its slenderness — effective height/thickness (he/t) The effective height may be taken 2s 0.75 x storey height if the wall is fully restrained at its ends, Where the wallis conngzted to a flexible floor element, the use of the full storey height is more appropriate. In CP110), walls are defined as ‘stocky" when he/t is les than 12, The design of walls which are more slender than this, should take into account out-of-plane moment transferred from the siabs and destabilising moment from eccentricity of axial load (see Section 3.1, page 18). ‘The minimum amount of reinforcement varies with the design requirement, A minimum percentage of 0.25% high yield steel (HYS) or 0.3% mild steel both horizontally and vertically is ‘usually required for shrinkage and temperature reasons. However, a larger percentage may be required for fire resistance (see Section 1.4) or seismic design (see Section 5.4, page 57), A meximum percentage of 4% is specified in CP110, CIRIA Report 102.RIA Report 102 1.4 FIRE DESIGN ‘The design of tall structures in fire is influenced by a number of factors: means of escape, containment of the fire, a minimum fire resistance of individual structural elements, and provisions for fire fighting without structural collapse. ‘There gre various rules in designing for fire safety in high-rise buildings which are defined in Table 1 betow'#?, These may be expressed in general terms as: 1. provision of more than one fire protected stairway with access at ground level 2. protected lobbies around access to lift shafts and stairways with wet riser main for fire fighting. (ry risers are often used in smaller buildings) 3. compartments of certain maximum plan area with floors and walls designed for the appropriate fire resistance period 4, passage of smoke and flame prevented through floor space and between compartments. ‘There are various additional safety techniques which may be employed (e.g. maintaining positive pressure in stairways and lift shafts to prevent smoke being drawn in, and the provision of sprinkler systems‘"*) and automatic smoke vents adjacent to the protected lobby). AA detailed review of these aspects is beyond the scope of this Report, and a study of References 3 and 13 is advised. Nevertheless fire criteria can impose significant constraints on the structural design process of tall buildings. In most cases, floors and walls are required to have 1 to 2-h fire resistance rating, and basement or storage areas up toa 4h rating, The minimum thickness of walls or sabs is controlled by thermal insulation requirements in fre), In order to conform to such a rating, CP110" requires that the wall be detailed with a minimum of 1% vertical reinforcement. The proposed revision to CP110("* permits a reduction in the amount of reinforcement for certain wall thicknesses where the wall is ‘exposed to fire on one side only (Table 2). The cover to the reinforcement should also be satisfactory for both durability and fire resistance, In the ACI Code, exterior or foundation walls are to have a minimum thickness of 200 mi, Table 1 Limiting height of buildings above which they are ‘treated as high rise for fire design Australia 25m France 28m Netherlands 13m UK Building Regulations 28 m Greater London Council 30m USA Building Code 23m New York State 30m West Germany 22m Table 2 Minimum thicknesses of walls for various fire ratings (aroposed revision of CP1 10} ‘Minimum dimensions (mm), exciuding any finish for a fire resistance of, Nature of construction and materials 3h | on Unreinforced oles than 0,4% reinforcement| dense aggregate (2400kg/m*) Reinforced 0.4 to 1.0% dense aggregate 160 | 200 | 240 “Lightweight aggregate (density 1250kg/m*) Reinforcement over 1.0% dense aggregate 130 | 160 | 190 ‘For concrete of densities between 1200kg/m* and 2400kg/m®, the value of all thicknettet may be interpolated, 13igure 3 Piled-raft foundation for shear wall 4 1.5 FOUNDATION DESIGN ‘The foundations should be such that they resist the loads developed by the building, and they should be efficiently located beneath the principal load paths, Uplift forces are rarely developed, because of the building and foundation mass. Small differential foundation settlements can alter the force distribution within the walls. The flexibility of the foundation can influence the dynamic response of the building, although this is not normally considered in wind analysis. Foundation types are clearly too numerous to describe within this Report. The type of piled-raft foundation shown in Figure 3 is most commonly used, depending on the sol eqnditions. Problems of piling and foundation design are reviewed in various CIRIA publications\**"*), In cases of seismic activity, liquefaction of certain granular soils should not be overlooked. 1.6 CONSTRUCTION FEATURES Mast modern core wall structures are constructed by slip forming in advance of the surrounding structure, In-situ shear wall elements are generally constructed along with the adjacent structure in shuttered lifts. In slip forming, cracking from early thermal effects is minimised because of the small time differential between concrete pours, In jump-form construction, the joints should be carefully prepared (o minimise subsequent joint slip. The construction speed of the shear wall buildings is normally controlled by the concreting and subsequent depropping of the floor slabs, Props should be left in place until the slab has achieved ‘adequate strength to resist further propping and construction loads, Where speed is important, permanent formwork methods are often used. Composite steel-concrete framed buildings surrounding service cores are popular in North America. Panel structures are generally assembled by looping or tying the joint reinforcement (eg.by couplers or welding) and grouting between the load-bearing faces of the panels. Particular problems include the requirement for construction tolerances, and adequacy of grouting technique for strength and durability (see Section 6), CURIA Report 1022. Categories of limit state 2.1.1 Ultimate strength 2.1.2. Instability ‘The design of shear or core wall structures may be considered at various limit states. These represent how the structure performs during its life, under the design loads with appropriate factors of safety, and under extreme loading events. For design purposes, these may be termed ‘serviceability’, ‘ultimate’ and ‘survival’ limit states, Each of the force actions described in Section 1.2 may contribute ther individually or in combination to analysis at the above limit states, ‘There are two components to the safety factor concept in limit state design. One is the load factor, ‘Yp for each form and combination of loading, F. The other is a material factor, 7,,, Which is applied {0 the characteristic value of material strength, S, such that LF <5/t—, w ‘This approach is amplified in CIRIA Report 63), Both factors vary with the limit state. Load factors, according to various codified sources, are presented in Table 3, Direct comparison between, ‘codes may be misleading, because of the different treatment of load and material factors in the overall factor of safety, 5/F. 2.1 ULTIMATE LIMIT STATE ‘This represents the attainment of limiting strength 6f the structure subject to the following provisions. Although force actions on the structure are based on ultimate (factored loads), and the capacity of the individual elements is based on their quantifiable ultimate strength, the forces within the structure may be determined elastically or plastically, depending on the capacity for redistribution of internal forces. Because of the uncertain or incalculable ‘post-elastic’ behaviour of some forms of shear wal, elastic methods are usually employed, In the design of each element, various load combinations may be required at the ultimate limit state (Gee Table 3). For example, three load combinations should be considered in the design of walls and foundations leading to maximum tensile and compressive forces, Walls may be designed in compression by conventional means (see Section 3.1, page 18). Various modes of failure of planar walls are shown diagrammatically in Figure 4, In coupled shear walls, onset of plasticity in the lintels is not in itself an ultimate limit state criterion, because considerable reserve of strength against overall collapse exists, However, by analysing the structure elastically, the potential for internal force redistribution can be assessed before the ultimate strength of the wall is attained, If the lintels do not contribute significantly to the structural action, they may be neglected at the ultimate limit state, providing they behave satisfactorily in service Its tacitly assumed that lateral restraints exist at each floor level so that lateral sway instability of the walls is prevepted. The walls may then be considered as braved between floors. In conventional structural theory‘, itis assumed that the restraining shear force at ground floor level should be 19 of the total vertical load (equivalent to a lower bound wind loading): In CP110), a value of 1.5% is used as an ultimate load, The lateral sway stiffness should also be such that the slope-deflection ‘under this uniform loading should be less than height/1000, This may be important for a series of parallel walls, as in Figure 2(i). In most cases, adequate lateral stiffness is provided by flanged or core walle, Fl Table 3 Load factors specified by various codes ‘Uma it state Serricebiity Sunil criio? acie7@? | ansaseit) cpio" ansess.i0? | ide. Regs | Act (proporea) vanptie, | ranpei7s, Paso, | oes +s. Lowy ssyys | 1100, +545 +B) +m) os.si4m, | osa.+isom, | 1250. +5, +m)} deem 0.1510, +51 +.)] with reduces oria3ey Imateral factors lapperas, | o2sinapy 41.95, Duo, 1am, | s1.20m% or 187841 +oam, Dy > neadween SL = Semicrorimromd oad, Ei + Fartgut lad, HL = Wind od CIRIA Report 102 1s2.2.1 Deflection 2.2.2. Crack durability 2.2.3 Human response to motion Shear tension. crack Yield in reinforcement 16 Flexural failure A related effect is that of enhanced moment resulting from eccentricity of axial load a tne design deflection under wind loading (commonly termed P65 effect). This may be taken into account by including in the strength analysis of the walls an additional moment of the total axial load times half of the design wind deflection (see Section 3.2.1). This rarely contributes more than 5% to the overturning moment, 2.2 SERVICEABILITY LIMIT STATE In design terms, the behaviour of a structure throughout its life may be represented as a check on the structural performance at the working load. In many cases, itis serviceability criteria which have the ‘greatest influence on the design of the structure. These may be expressed as the criteria of deflection, cracking, durability, and human response to vibration. Fatigue is rarely a design condition for reinforced concrete elements. ‘When considered as a quasi-static displacement, the lateral deflection of shear wall structures is important because partitions, windows, or lifts, etc. are sensitive to sway. For most structures, maximum displacement of height/500 is usually acceptable to avoid visible distress, or impaired ‘operation of lifts, etc. but, for high-rise buildings, a displacement limit of the order of height/1000 may be required for acceptable movement at the top of the buildings. ‘The permissible vertical deflection of floors depends mainly on the cracking of partition walls and lading, Deflections of reinforced concrete slabs and beams are both from imposed loading and long-term creep effects. Maximum span/depth ratios of floor elements are specified in CP110°), CP110 requires that crack widths should be limited to 0.3 mm under normal circumstances, or 0.2mm. where the structure is exposed to an aggressive environment. Cracking is most severe in the arca of the wall to lintel connection. Crack widths may be calculated using Clause A.3 in CP110"") as a function of the strain in the reinforcement. Durability is also dependent on the quality of the concrete, particularly where walls are external to the building, It is necessary to control the mix proportions, and to achieve adequate cover to the reinforcement and compact placement of the concrete on site Until recently, comfort criteria have often been overlooked, because of the lack of performance data for design, but in many instances they are of paramount importance. The magnitude of peak acceleration required to initiate adverse comment from the occupants of a building at a particular frequency can be extremely small (of the order of 0.5% of the acceleration of gravity). The stipulation of a reasonable serviceability criterion is somewhat subjective, and it depends both on the use of the building and on experience gained on similar buildings in-service. In most circumstances, adverse comment from a significant number of occupants (say 10%) within a period of recall of, say, 5 years may be an acceptable comfort limit. The threshold of perception to more frequent movements is much lower, and itis hightened by accompanying noise. Quantification of the structural response to excitation and the accompanying comfort effects are presented in Section 4.4 (page 47). psn Horizontal shear Vertical shear 1re 4 Possible wall failure modes CIRIA Report 102,Figure 5 Forces developed ‘asa result of panel removal CRIA Report 2.3: SURVIVAL LIMIT STATE The integrity of the structural form should be such that it can withstand extreme loading events ‘without collapse. These events may result from explosions or wind or earthquake loading greater than those normally considered in design. Where the structure has little or no redundancy, it cannot continue to resist load after failure of one element. This relatively new concept is termed here ‘survival limit state’ ‘There are a number of approaches to ensuring structural integrity. One is to design all elements for the loads received during such extreme events. Another is to develop alternate load paths following removal of a critical element. Both these may be quantified using reduced load and material factors (see Table 3). It is necessary to ensure that all elements are adequately tied so that unusual force actions can be resisted and catenary action of floors can be mobilised as in Figure 5. Such tie force requirements are presented in the ACI) and CP110™) codes, Fire engineering has recently developed along these lines in that the reduced strength of concrete ad reinforcement fora given ire rating may be related tothe loading applied tothe member at this eu ‘survival’ limit state. Reference to the Institution of Structural Engineers Report‘) is recommended. Tie forces ! L Longitudinal T Transverse V Vertical P Peripheral 73. Elastic design of shear and core walls Cantilever walls, as defined in Figure 1. behave in a predominantly flexural manner, whereas squat ‘and short walls act more like deep beams in which internal forces are dependent on compatibility of ‘axial and shear strains within the wal elements. In this Section, methods of analysis for cantilever walls are presented. Their behaviour is often governed by the presence of a regular band (or bands) of openings. Although the force actions within the structure are determined elastically, the ultimate strength of critical elements under factored loads is generally based on ‘plastic’ analysis of the strength of a particular section according to conventional reinforced concrete design, Elastic methods may therefore be used for both ultimate (factored) load and working load design, 3.1. DESIGN OF SLENDER WALLS IN COMPRESSION ‘The treatment of slender walls is presented in CP110) in the same form as for columns. This is ‘based on the ultimate strength under axial load and out-of-plane moment. Depending on the load combinations of in-plane moment and axial load, (Figure 6(a)), the section of the wall under ‘maximum compression is then assessed as a function of its slendemess—height/thickness (he/t). Above a limiting slenderness of 12, an additional moment resulting from eccentricity of axial load is to be applied, The maximum slenderness of a wall with less than 1% reinforcement is 40. This additional moment, Ma, is eqiV1 where values of ¢, are presented in Figure 6(b). The out-of-plane ‘moment is also dependent on the moments transferred from the slabs, which may be a significant factor at external walls or where adjacent floor spans differ. The out-of-plane moment to be considered in design is given by M=04M +06 Ma +My tM2 @ where My and Mp are the moments applied at the slab connections such that Mz>M, or 0.0SNt. ‘The wall design is then to be checked using the column design tables in Part 2 of CP110 in terms OfN/N, and M/My, Ny is the ultimate compressive strength of the wal in the absence of moment and equals 0.45feyAc + 0.75Agfy, where A, is the total area of reinforcement. My is the ultimate moment of the wall considered a a conventional reinforced concrete beam. Walls with returns such as flanged or core walls asin Figure 6(c) are not specifically covered by the above requirements in CP110. Cleary, the use of the above slenderness criterion is conservative in such cases, Some guidance is given by the American Portland Cement Association) for walls designed for non-seismic loads. If the outstand length of a wall is less than 61, it may be considered to be fully restrained against out-of-plane movement, independent of the distance between floor restraints, This is discussed further in Section 3.2. eft} 2 | 0 5] ol ex 008 O12 021 039 O46! O81 LL L ei (b) Additional moment factor in CPT10 Wall partially restrained, wyst LE Section h-A rath Wall onrestrained 7 wchfs Axial forces 1 in walls oe ae {a} Force ations on plane walls {c) tenderness reduction for on-planar walls Figura 6 Design of reinforced concorde walls in compression 18 CIRIA Report 1023.2. DESIGN OF WALLS UNDER AXIAL LOAD AND MOMENT 3.2.1 Elastic analysis The equivalent axial force on the extreme fibres of a wall may be calculated elastically for combined of planar walls axial load, N, and in-plane moment, M (see Figure 7(a)), and the ultimate strength of the outer section of the wall checked as an equivalent coluran (see Section 3.1). When the line of action e(=M/N) of the applied force exceeds one sixth of the wall Iength, L, the outer fibres of wall may crack in tension and the overturning moment is resisted by the vertical reinforcement. In such cases, the neutral axis position x (for x12t), It follows that a slight strength reduction is necessary (see Section 3.1). For design purposes, this may algo be considered as a reduced effective width of wall, No information exists ‘on the stability of walls (eg. webs of channels) with variable axial stress along their width, In such ‘cases, the use of Equation (7) is suggested Its not certain what length of wall return is required to stabilise the edge of the adjacent planar wall, The stability of a stiffened wall can be assested by simple theory from the inertia of the outstand, including an adjacent section of wall equal to its depth. As a simple rule, for wall lengths up to 30/, it may be assumed that the outstand should be greater than 20% of the wall height in order to be effective in stabilising the wall at its ultimate compressive strength (i.e. hy < 121), These design rules are summarised in Figure 6(c), page 18. Inherent in the analysis of Section 3.2.1 is that ‘stress strain’ relationships of concrete and steel are effectively linear, and that yielding does not occur. The postlastic stress distribution is of the form shown in Figure 1(b). To take account of the reserve of in-plane moment capacity beyond the elastic limit, permissible concrete and reinforcement stresses of 0.45/ey and 0.87/y, respectively, may be used in elastic analysis a ultimate loads with an enhanced value of the modular ratio, The ultimate strength of walls in compression and bending is reviewed in Section 5.1, page 49. 3.3. ELASTIC ANALYSIS OF PIERCED SHEAR WALLS Rieoed shar wall may be analysed by elute methods in which the exit 9 coupling beams Gintels) between wall elements is represented as a continuous flexible medium™), The basic equations of equilibrium and compatibility of the shear wall elements under lateral loading may be presented as follows. For a single line of openings, the moment resisted by a wall element at any height from the base of the wall is: CIRIA Report 102CCIRIA Report 102 My= (Mo — MI 1h +12) o where J, and J are the inertias of walls 1 and 2, respectively, about their centroids, Mg is the moment from the applied lateral loading at that level, and T'is the axial force in the wall which is given by Te (Made ao) ‘The shear force in the lintels, g, is a function of x for which a typical variation is shown in Figure 10. The compatibility equation relating 7 and M is such that the deformation of the lintels is given by -8¥ (uy tug) gho® ore THT. a ‘The geometrical parameters of the wall d, 4, and I are defined in Figure 10 and J, is the inertia of, each lintel, The vertical and horizontal dispiacements of the wall (u and ») are given by Sha sE MIE (hy +) dx a2 uy = SS TBA, Ax ete. for uy a3) The subscripts to the wall area, A, and displacement, u, refer to walls I and 2, respectively, Solving the resulting differential equation yields an expression for q which isa function of the form of lateral loading. “ By lifer lati aration 5 Bel ead f lintel farces.g Figure 10 one (b)Detormatio of tite3.3.2. Solutions for different load cases 4 Considering first the effect of a single point force, Py, at level, x, the resulting forces in the Lintels and walls (at point x) are given by the general expression in terms of x and x, in Appendix 2. There are two principal parameters which define the performance of the wall. These are and B, which depend on the geometrical properties of the walls and lintels and on the number of lines of openings. For a single line of openings 12 P= eRe «aay a -£ fF + 4p saad +] as) ‘The geometrical proportions of the wall are often presented as a factor, u, where, =a? / (§ 4). Typical values of range from 1.1 to [.6. For two symmetrical lines of openings, the parameters teoome au, as POF The Lf pe een en /Ad (Gy ‘These equations for g, T and » reduce to a more manageable form when certain common loading conditions are considered. These are: point load, P, at the top of the wall, uniform loading, w, and triangular loading of maximum value, w, at the top of the wall. These solutions are also presented in Appendix 2. Further simplifications are justified when af>4 as cosh aif * sinh a i. ‘The moment sharing between components M and 77 varies with the degree of coupling action, for which extremes are indicated in Figure 11. It remains to find the force in, and the position of, the ‘most highly stressed lintel. This is facilitated by the use of the design charts in Figures 12 and 13. ‘The forces attracted to the lintels increase with aif. As the coupling between the walls increases, so the position of the most highly stressed lintel moves towards the base of the wall. For comparison, ‘the maximum shear flow in a solid wall is 1.5 x shear force/wall width. The proportions of most shear wall buildings are such that 4 sd as) where d is the depth of the lintel, The influence of shear deformation may be included by modifying ‘the lintel inertia? according to the factor = Te | (1+ 2.4 (a0?) 20) All elements may be taken as uncracked for an initial elastic analysis. This is a reasonable approximation, because only a proportion of the lintels are highly stressed, and, even if cracked, their effect on stress redistribution is small if they are adequately reinforced, Nevertheless, it may sometimes be necessary to assess the sensitivity of the structural behaviour to a range of lintel stiffness. In such cases, the cracked inertia may be calculated from the formula Te = tx,? /3 + pmdt (d ~ x, an where the neutral axis depth, xe, is given by 22 xeld = — pm [(om) + 2pm being the proportion of top or bottom reinforcement in the section and m the steel-concrete ‘modular ratio (Section 3.2.3), Some allowance for tension stiffening is often made by averaging the cracked and uncracked inertas, ‘The behaviour of flanged wall is no different from that in Section 3.1 (page 18), except that the dimension, /, is to the centroid of the wall elements, and J and fp represent inertias of the various flanged sections. Coupling action between walls can be developed by slab bending in the absence of lintels, Recent analytical studies by Coull and Wong’ show that a certain effective width of slab may be included in the analysis. Because of the many practical configurations of walls and slabs (eg. end walls, internal walls, and core walls with slab openings), design graphs are only presented for a number of standard cases as in Figure 16. Because coupling by slab action is not efficient (see Figure 8, page 20), it may be advisable to neglect this action at the ultimate limit state, provided that a serviceability check is made on the degree of slab deformation, 3.3.4 Detailing of In the analysis of the previous sections, it was assumed that all elements were uniformly reinforced. pierced shear walls In theory, the lintel reinforcement can be detailed according to the shear flow diagram of Figure 10 (page 23), so that all intels would reach yield simultaneously. However, in practice, the behaviour of the structure cannot be predicted with such accuracy, and it is not efficient to schedule such a large variation of reinforcement details. Therefore, inelastic design, it is common practice to detail ‘asmmall number of bands of lintel reinforcement with height, making sure that the position of the ‘most highly stressed lintel as in Figure 12 or 13 is not sensitive to changes in the design parameters (c.g. aand §). A maximum reduction of 20% in the peak lintel moment may be made, provided that the excess moment is spread across the reinforcement band. Reductions greater than 20% may affect the elastic behaviour, in which case the elasto-plastic behaviour should be examined (see Section 5.2, page 52). The distribution of vertical stresses in the walls can vary significantly with the lintel stiffness, as is apparent from Figure 14, One wall element is predominantly in compression at ultimate loads, whereas the other isin tension, and it is therefore cracked over a significant proportion of its length and height. In such cases, extra bars may be detailed at the outer edge of the wall for maximum effect in resisting overturning. The variation of vertical reinforcement with height should also take into account the sensitivity of the stresses in the walls to aif, ‘The shear resistance of a wall may be assessed as a cantilever beam in which the vertical reinforcement acts as a tensile reinforcement and the horizontal reinforcement as shear stirrups ‘The minimum reinforcement is 0.25%, The effect of axial load superimposed on the bending action is to increase the shear resistance of the concrete. Tension reduces the shear resistance, For wind analysis, shear is rarely critical, even ignoring axial compression. For seismic analysis, redistribution of shear between walls of up to 30% may be permitted, provided the walls are of adequate ductility. ‘CIRIA Report 102 29Figure 16 Effective slab widths for various cases 30 22 yi 2 28 30 CIRIA Report 1023.4 STRUCTURAL INTERACTION OF SHEAR WALLS. 3.4.1. Effect of plan The loads attracted to each shear wall element are a function of their position and their relative distribution of walls stiffness. The simplest assumption is that the floors are rigid in plane, and that the stiffness of each. ‘wall can be represented by a single parameter,X;, The centre of rotation may be determined by simple statics along an axis, y measured from an arbitrary reference position on the building face as in Figure 17, such that: FREKyyi/ EK; 23) ‘The force per wall, j, resulting from a total force, P, acting at point yo on the face of the building may therefore be given by = PK) | EK} +P Qo ~3)¥j | (EK; 0) ~ 3 + EKQ)) oa Except where there are cores without substantial openings (see Section 3.5), the torsional stiffness of the walls Kj, may be neglected. Because the deformation of a coupled wall unit is a result of both bending and shear, the stiffness parameter, K, cannot be Uniquely defined forall eight positions. Therefore 9 varies with height, For reference, K may be calculated by applying a unit force at the top of the wall. Using the formula for displacement, vin Appendix 2 (Equation (72)),K is then Plv (or x= x= #0) ‘This simplified approach is valid where the centre of rotation is close to the centre of the building. In other cases, the analysis of Sections 3.5 and 3.6 may be more appropriate. It is sometimes assumed, that K may be directly related to the in-plane inertia of the wall. This is not of sufficient accuracy {or walls which are partially coupled, and itis only appropriate for solid walls or for walls with low coupling (aif <0.5), where the behaviour is mainly flexural 3.4.2 Interaction of The interaction forces between walls may vary significantly up the height of the building, because frames, walls and cores _ of differences in the deflected shapes of walls with nominally similar stiffnestes. This Variation is accentuated by the interaction of different structural forms (e.g. walls, cores and frames). In the ‘example shown in Figure 18, the load sharing between the three shear-resisting elements is equal according to the simple theory above. ‘However, frames deform in an almost pure shear manner, whereas walls or cores deform in a shear- flexural mode, depending on the degree of coupling. Because of this, the frame sheds load at its base where it is more flexible, and the core attracts load. Although the distribution of load intensity among the clements is therefore far from uniform up the building, the total shear force resisted by each varies by a smaller amount, Plan on level / . Centre of rotation Figure 17 ‘enavour of Leading at shear wall building Level i) CIRIA Report 102, 31Figure 18 Load sharing between elements of nominally similar stiffness 3.4.3 Three- dimensional analysis of shear wall building 32 McLeod’? proposed that the shear force at the base of each lateral load-resisting element may be predicted as a first approximation by considering a single interaction force at the top of the building. ‘This is equivalent to load sharing in terms of relative stiffness. The shear stiffness of a frame building of height, /1, may be given by + wy hy where Ze and fy are the sum of the inertias of the columns and beams, respectively, on the lowest bay of height, and beam span, !. Because there may be a variation of Zz with height, a reduction, factor, kc, may be introduced given by sy ke = logaci(e~ 1 026 where ¢= top ile vottom ‘This simplified analysis tends to underestimate the shear force on the element possessing the more flexural behaviour (e.g. core). In most cases, the stiffness of frames is small in relation to walls, and ‘therefore the frame is constrained to follow the displaced shape of the wall. One exception to this ‘may be where mullions around the perimeter of a building are closely spaced. In such cases, the load ‘which they attract may need to be considered in design. Coupled 1 we 1 ws Coupled Frame Core or val plane wall (a) Plan view {) Deflected shapes ype od > > ~~ ‘Simplified > load sharing > s 0 wi (c) Load sharing between walls Toad intensity per wall ‘The simple ‘spring’ method above may only be valid for an initial assessment of the load distribution in a complex building or where the shear wall behaviour is predominantly flexural (ie, walls are not pierced, or lintel coupling action is small), A matrix solution for the three-dimensional analysis of ‘shear wall building was developed as follows(),It is very efficient in terms of computer storage, because it utilises the general wall force — displacement relationships (Appendix 2). The equilibrium of the overall structure may be defined by the matrix equations: (PI an 5, (2) +83 (0) (T1= 5) (21 +53 101 +54 (61 8) CIRIA Report 102Figure 19 Variation in contre of rotation of typical building where [Z] and {0} are column vectors of floor displacement and rotation to be determined at cach reference level, , which are defined as occurring at an arbitrary plan reference point. [P] and (71 are column vectors of applied lateral load and torque defined as relative to the same plan reference point. To avoid complications in the sign of the loading, this reference point is normally taken as at the extremity of the building (see Figure 17), The matrix stiffness parameters 6 to 54 are given by the matrix operations for the / walls on plan, as 52 Bs= Zi Filh (YI? 4 61-3) UF 2 lal} 41 9) 2 (Fol [2] is ani x/ flexibility matrix for each of the / walls considered independently in the 2 direction, ‘This may be evaluated from Equation (72) of Appendix 2, by applying a unit force at each level, xj, and determining the deflection at all other reference levels, x.5, therefore represents the sum of the inverted flexibility (Le. stiffness) matrices ofthe j walls. [¥4] ig a row vector defining the position of each wall relative to the plan reference point (Figure 17). [F@* is a square matrix of rotational stiffness coefficients for each wall, Solving for [2] and [8] is by the matrix operations: 10) = (82 611 62 +53 +54)" [-52 54 i+] G0) [2] = (-@3 +54) 527 5, +82) [-G3 +54) 527 (7) +171] 1) These column vectors are computed by matrix multiplication of the above terms. The forces on each, wall at level fare therefore given by fy = [121 +001 04) J eet (32) (r= (6) (Fel;* G3) This method may seem complex, but it can be performed relatively quickly, using standard matrix inversion and multiplication subroutines, ‘The geometrical proportions of each wall (i.e. 1, A1, Ie. h, bt, H, ete) may be input, together with their positions (y, 2) relative to the plan reference point. The applied loading on the face of the building may also be chosen accurately rather than fitting the constraints of a standard design chart. The torsional stiffness of most planar walls may be neglected, except that of core walls which may be calculated using the torque-rotation expression of Section 3.6. The parameter [Fg] also represents the contribution of those orthogonal walls which, by virtue of their distance from the y axis of the building, have a rotational stiffness component. The accuracy of this method naturally increases with the number of reference levels, used in the computation, However, itis usually found that the use of five reference levels is reasonably accurate, and therefore the maximum matrix size is S x S. The use of this method is illustrated fos 4 complex building in Figure 19, where the change in the plan centre of rotation has been plotted 3m 30m mt 3.0m K 12m x Arbitrary reference | ene Position of centre of rotation relative to arbitrary reference 3334 3.5 COMPUTER MODELLING OF SHEAR WALL BUILDINGS ‘The difficulty in analysing shear wall buildings which do not conform to a relatively simple model means that computer simulation methods are very attractive to the designer. Finite element methods are expensive and time consuming where relatively simple force distribution output is required. Frame or discret line clement methods offer the advantage of being simple and relatively accurate, One such model, as proposed by McLeod, *) is shown in Figure 20, where rigid wall elements are used to connect the lintels to the centre of the wall units. These methods are particularly useful ‘where there are variations in openings or wall sections, ete. which cannot be analysed theoretically Such methods were principally developed for two-dimensional analyses, using the parameters A, and I, as presented in the previous sections. However, ill conditioning of the matrix computation ‘can occur if the relative stiffness between elements is greater than about 1000. To observe geometric requirements, line elements should be positioned at the centroids of the walls which they replace. ‘Thi ‘wide-column’ frame method may be used to model three-dimensional elements such as cores'3"), as in Figure 21(a). The horizontal wall elements are of high inertia but low torsional stiffness, o that warping at the corners is not inhibited. It may be necessary to constrain the ‘geometry of the core by using bracing elements of relatively high axial but low bending stifiness. Whole buildings may be analysed in this way by interconnecting comer nodes by floor-bracing clements, also of high area, as in Figure 21(b). In-plane loading on each of the floors may be considered as an equivalent transverse force and in-plane moment applied at selected braced nodes. Refinements to this method are those of mesh generation of a typical floor grid and constraining nodes on each floor to move in a rigid body fashion, thereby reducing the data input. 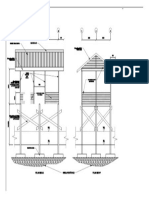Graphical plotting of the assembly of members also aids checking. One such example of a 43-storey ccore wall building with external mullions is shown in Figure 22. cea ae beam LA Rigid element Coupling beam ha hay LAr Support beam _Fotium floor Figure 20 ‘Model of shear wall by discrete line elements Foundation spring CIRIA Report 102Stiff element (high inertia, low torsional stiffness) Element with properties of wall Corner node Element with properties (area only) of intel {a} Analysis of core wall by Line elements Core modelled Slab bracing elements as at left (area only) Equivalent load al nodes Uniform load (b) Representation of slab by line elements Figure 21 Representation of complete building by line elements Figure 22 Computer model of shear wall ‘building (Courtesy Ove Arup & Partners) CIRIA Report 102 353.6.1. Flexural behaviour of core walls 3.6.2 Torsion of core with symmetric ‘openings 3.6 ELASTIC ANALYSIS OF CORE WALLS In bending, core walls may be analysed as channel sections or as coupled flanged walls, depending on the direction of bending (sve Figure 23), Because such cores are often used for services and lifts etc., the area within the core is usually heavily voided, and lintel beam depths are shallow. Coupling action across wide openings is therefore limited in many cases For a channel with an asymmetric distribution of openings, such as Example (i) of Figure 23, loading through the centre of the section causes both bending and torsion about the shear centre of the core. The postion ofthe resultant shear centre ofthe section varies with the degree of coupling, and as the coupling increases the shear centre moves towards the centre of the core. When loads are applied through the shear centre, the bending stiffness of the wall isthe sum of the stiffnesses of the channel and coupled wall sections. However, the position of the shear centre is usually indeterminate. It may be reasonable to assume that the shear centre varies linearly between the cases of all = 0 and 16 (ig), where off is determined forthe piereed section ofthe core, Ideally, the torsional forces on cores should not be as significant as the bending forces by careful ‘choice of their plan distribution (see Figure 2, page 11). Nevertheless, a nominal eccentricity of lateral loading should be considered, particularly in the design of buildings with single cores (Gee Section 4.3.5, page 47). The torsional analysis of cores with different distributions of openings is complex, and the discrete element method of Section 3.5 may be preferred in many cases. However, it is possible to analyse) the case of torsion of a core with a symmetric disposition of openings as in Figure 24(a), The controlling differential equation is: #0 ae 28 _ Pal = onjtors>xor0 torn, Single opening > Uncoupled Coupled (ii) Coupted (iii) Asymmetcic (iv) Channets in bending and torsion flanged walls channels about shear centre(S.C.) sections Figure 23 Behaviour of core walls in bending 36 CIRIA Report 102‘The warping displacement causes bending moments in the lintels, Mc, given by Me = ELLD , 28 (+p) 66) oe dx 3.6.3 Torsion of ‘The general case of a core with a single line of openings as in Figure 24(b) was analysed by Coull(™?, cores with different The method involved calculation of the warping constant of the channel section by a folded-plate i analogy to be input into the controlling differential equation above. The method has also been opening arrangements CTtended to other cross-sectional shapes, This method isnot repeated here, Nevrtheles, he constants 7? and {2 can be calculated explicitly Irwin and Bolton) also present a design method for a core with a single line of opening which is based on an energy method. A computer program listing is available (held by CIRIA) to determine the torque-rotation flexibility matrix [¥9) for use in the analysis of Section 3.4.3. x CAD? waving Warping displacement displacement Slab {a) Two openings () Single opening Figure 24 Behaviour of two forms of core walls in torsion Shear centre of single channel Figure 25 Geometry of core with channel walls CCIRIA Report 102 374. Dynamic analysis of shear wall buildings 4.1.1. Flexural modes 38 ‘The stiffness of shear wall buildings is often such that their natural frequency is higher than that of framed structures. This is favourable as regards wind excitation, but not necessarily so in determining the response to seismic action. Some estimate of the dynamic response of the structure is usually required, not only to determine if the quasi-static wind forces are enhanced by wind gusts, but also to ascertain the comfort of the occupants of the building to such excitation. ‘The most important structural parameters are the natural frequency and the damping of the vibration. Because of the stiffness of non-load bearing elements and partitions, the measured natural frequency of the building is usually greater than that used in design. However, at larger amplitudes of vibration, these elements are likely to crack and lose their stiffness, and thus cannot be relied upon in aan ultimate load analysis, 4.1 APPROXIMATE CALCULATION OF NATURAL FREQUENCY From measurements of the response of shear wall and framed buildings, simplified relationships have bbeen developed to calculate the natural frequency from the geometrical proportions of the building, Examples of these formulae 9g collected from various sourcei(*) are given in Table 4. In Table 5, ‘these formulae are compared'*”? with more exact methods (Section 4.2.1) as calculated for a typical shear wall building (Figure 19 page 43) of measured natural frequency 1.3SHz, In Table 6, measured ‘dynamic properties of various shear wall buildings are presented\**) which correspond to relatively low levels of vibration excitation (and hence damping). Af the building is treated as a cantilever of uniform mass per unit height, m, and bending stiffness, EZ, its natural frequency in the plan direction, z, is given by $2 = 0.34 [KyitmHy, where Ky = 3E1/H° en In this case, m is expressed in mass (kg) rather than force units (N). This is 1.5 times the frequency of the case where half the total mass is lumped at the top of the cantilever, This solution assumes that the wall displacement increases roughly parabolically with height. The deformation of a coupled shear wall may approximate toa linear displacement with height for which the above constant reduces to 0.28, ‘The ‘equivalent spring’ stiffness parameter defining the behaviour of a coupled shear wall may be ‘represented by the term Ky = 1/v, resulting from a unit force applied at the top of the wall, This is calculated from the expression for v (with x = x; = /1) in Equation (72) in Appendix 2. Insexting Kiq into the above equation in place of the equivalent stiffness of a pure cantilever and assuming a linear mode shape gives fi Framed buildings deform in a shear mode for which the above constant reduces to 0.23. Their sway stiffness may be calculated from Equation (25). .28 [Rulon 38) Table 4 Approximate methods of estimating the natural frequencies of buildings") =a Formula for Structural form ava natural frequency(Hz) of buildings 1 a6 General | 2 101M, Frame buildings 3 34/H(Lw/Lp)** ‘Mixed frames and walls. 4 slo ire aoi Shear wall buildings Ss qipDyH Shear wall buildings 6 1icg40.018H) General 3. ys the number of storeys of height, 44. LBs che total Length ofall frames indirection of period estimation (m) 5. Ly isthe total length ofall walls, as above (m) 66. risa foundation parameter varying from 0 101 (CURIA Report 102,Table § Calculation of natural frequencies of building in Figure 19 ‘Computed natural frequencies, fy (Hz) No, of Mass | reference | Modet Bending Torsion case levels 2 3 1 2 3 a 20 A 174 | 962 | 257 | 157 | 7.79 [ 200 > 20 A iss | 834 | 220 | 149 | 7.20 | 183 e 20 A 13s¢ | 736 | 194 | 132 | 639 | 162 4 20 A 108 | 602 | 160 | 128 | sis | 15.7 © 10 A 134 | 720 | 190 | 128 | 621 | 15.7 © 2 A 126 | sso | - | 12 | 4.76 ¢ 20 B oss | sos | 132 | os: | sas | 144 S 1 084 - = e - 4 0.80 2 z= z= 7 - = 5 ce - S : - Noes: 1. Model A is that of Section 4.2.1, including all stractoral interaction 2, Model B ignores coupling action of beams. 3. Mase case a ~ bare structural mass 44. Mass case b ~ structural mass plus allowance of 2 KN/m? for finishes ete 5. Mass eae ¢ — as above, pls half impored load, 6. Mate eas d — a case by plus total imposed load (S kN /m?). 7. Models 1,4, and 5 from Table 4 8, Measured natural frquency is 1.35 Ha Table 6 Dynamic properties of various high-rise buildings Dimensions (m) [Average] Fundamental] Damping Building Density|Frequency(Ha} —(%) Location eight] Widen [Leng Notes x | ¥ fosim?y | xx Py [xx | vv 1 Hawai, usa [100 | 23. | 23 | 273 Joe or fia [141 | shear waits 2. Sheffield 80 | 20 | 36 | 337 | 068] o87]08 |09 | corewith mullions 3. Prague 63 {12 | 30 | 338 Jo83] 133} 1.0 | 10 | Precast shear wall 4. BREtest building! 48] 18 | 31 | 284 |o96 1.16] 1.0 | 0.8 | Modet structure 5. Wrexham 43 {13 | 13 | 323 J 147] 1s9}os | 10 | core wall 6. Los Angeles 30 | 97] 20 | 333 Jo.72}310}35 | 20 | Frame,shear wall 7. Plymouth 47] 122] 45 | 226 | 132] 125} 10 | 41.5 | core, shear wall Lote: All ata ae taken from reference 38 CIRIA Report 102 394.1.2. Torsional mode 4.2.1. Analysis model Figure 26 Lumped mass representation of ‘coupled shear wall 40 ‘The torsional behaviour of the building may also be important where the centroid of the shear resisting elements is eccentzic to the centre of mass of the building 5), The layout of the walls therefore has a significant effect on the torsional response. Coupling between flexural and torsional ‘modes occurs where the vibration frequencies are similar (see Section 4.2) ‘A torsional stiffness parameter may be defined by the expression: Kg = 2K9;+ 2K,)? + 2Ky2? a9) where Ky and K; are the equivalent spring stiffness from unit forces at the top of each wall in the ¥y and z directions, respectively, y and z being the plan coordinates of the wall relative to the centre of rotation of the building. The torsional stiffness of all wall elements, Kg, may be neglected, except those of core walls, which may be calculated from Equation (82) in Appendix 2. The torsional mass. of the building per unit height about the plan centre of rotation is defined by its mass radius of gyration, rg: Assuming a linear variation of rotation with height, the frequency of the first torsional ziode is approximately’ 19 = 0.28 [Kemrg*) (40) Higher modes of torsional vibration are rarely important in wind action. If the building comprises a series of frames or walls of equal stiffness, the fundamental torsional frequency is the same as that (of the first flexural mode, If the shear-resisting elements are concentrated at the extremities of the ‘building, the torsional frequency is roughly 1.7 times that of the flexural mode. 4.2, DYNAMIC RESPONSE OF SHEAR WALLS ‘The analysis of complex shear wall buildings is usually performed by computer simulation. The frame model proposed by McLeod‘? (see Section 3.5) may be utilised, and the lumped mass of the wall, slab elements and vertical imposed loading applied at the modes as in Figure 26. It is probably reasonable” to take an average of 50% of the design imposed vertical load as an ‘equivalent mass for dynamic analysis (see Table 5). The full mass of any plant or fixtures should be included. This two-dimensional analysis is satisfactory for rectangular buildings comprising a number of similar parallel walls, The stiffness of the foundations may also be included by an equivalent spring analogy, The fundamental frequencies in both y and z plan directions should be calculated, ‘The coupling between torsional and flexural modes is indicated) in Figure 27, in terms of the resultant frequency of the system, fy. The dashed lines represent the fundamental frequencies of the modes when uncoupled. The term ey/r9 isthe distance between the plan centre of mass and centre of rotation divided by the radius of gyration of the building mass about the centre of rotation. When 1-25 > f,//o > 0.8, itis reasonable to assume that the modes are uncoupled (i.e. fa = fx OF fg)» Fora detailed dynamic analysis of complex buildings, the method of Section 3.4.3 (page 32) may be utilised. Lumped mass M Parabolic Linear Actual Base Flexural Base Shear- spring rotation flexural = Frossile mode shapes ————» CIRIA Report 1024.2.2. Damping ratio Figure 27 Effect of torsional properties ‘on natural frequency of building CIRIA Report 102 The angular frequency of each mode, Wa, may be calculated from the determinant of the following matrices on the assumption that flexural and torsional modes are uncoupled: War FF we? 1 ° an (tay* [Rol — wa? where [1] is a unit matrix, and flexibility matrices [F,] and [9] are the translational and torsional ‘components summed for all wall elements. Usually, no more than the first ten reference levels are necessary for an accurate analysis”), and the first five frequencies (w,/27) need be output (see Table 5, page 39). The stiffness of the foundations can be introduced by adding a matrix of the form [Xxx] to [Fal where Ky is the overturning stiffness (M0) of the foundations. In most cases, it is reasonable fo assume that the foundations are rigid. The calculation of the flexibility of piled foundations is reviewed in Reference 40. The effect of coupling between the modes is that torsional motions are induced by lateral excitation. The building in Figure 19 (page 33) may be expected to show significant coupling between torsional and flexural modes, with a consequent increase in plan displacements, For buildings with small values of e, /rg, torsional modes are not usually critical, although sill excited by torsional loading. For dynamically sensitive structures, this parameter should be minimised. ‘The response of the structure to the vibration excitation is influenced by the degree of damping, which may be as a result of both aerodynamic and structural forms. Where load- 4f, the vibration is said to be ‘Torced’ or ‘quasi-static’. In general, the structure consists of a system of masses, and several structural frequencies may ‘contribute towards the total dynamic response. The modal participation factor describing the relative base shear froin each of the j modes is defined by the term hese ieee (4a) THO my dx where @; is the mode shape, normalised to unity at its maximum value, and m; is the lumped mass of each node. The induced force at egch node, i, for each mode is. ag =6,G;RU}), and the forces are combined according to qi = 2 aq" In seismic analysis, SU) is often expressed in terms of base acceleration (a is RU). Therefore the nodal force is determined by the nodal mass times \K(/n) In wind analysis, gustnes is presented in terms ofthe variation of wind speed. The input spectruh fs the power spectrum of gust velocities ‘S\(/) defined such that OW) fe SWD.aF (45) where o(¥/) isthe root-mean-square wind speed. The root-mean-square structural response, o(Q), relative to the force, O, induced by the mean wind speed, V, is given by oQ) 2 4 ISMN Z2 a (46) oe ‘This form of analysis is only possible where an accurate time history of an event is available. Its principal use is to calculate the actual structural response to specifit seismic records. The input ‘wave, which may be in the form of acceleration, displacement, etc. is divided into its component frequendigs over a short time interval, and the response is calculated by time-step integration methods), These methods are very’ expensive in computer time, and they are generally only used ior special structures, 43 WIND LOADING ON BUILDINGS The modern description of wind is by a terrain category defining the surface roughness. In the Code of Practice for wind loading”, the terrain description ranges from open countryside to city centres. This ground roughness reduces the atmospheric (or gradient wind speed, Vg) to a mean value Vio at a reference height of 10m above ground level. The mean wind speed at height x is then given by the power relationship V = Pio (x/10)® For the calculation of design loadings, the 1-in-50-year recurrence wind speed is normally used. For appraisal of in-service conditions, a shorter period of recurrence may be more appropriate. ‘Typically, the yearly recurrence design wind speed is about 60% of the 50-year value, increasing to 80% for the S-yearly recurrence wind, Harris“) introduces a factor, Zo (roughness length) which defines the mean wind speed in relation to the gradient wind speed for each terrain category. Typical values are Z, = 0,003 (fat, ‘open country), 0.03 (rolling country), 0.3 (outskirts of towns), and 0.3 to 1.0 (centres of large towns). CIRIA Report 102432 Structural response to wind action CIRIA Report 102 ‘The usual parameter for defining the design wind speed is the 3s gust value V3 for which values are given in the Code“? appropriate to flat open country. This represents a measure of the instantaneous wind speed averaged over a 3-s duration, As wind is composed of a mean (V) and a variable component of velocity (gust), itis apparent that the ratio V3/V increases with increasing, terrain roughness, Other averaging periods for the wind, such as the 15-6 gust, naturally result in smaller average wind speeds than V3, as tabulated below. The exponent a also varies with roughness factor, Zo, In the Code), the effect of ground roughness and building size is presented in terms of a factor Sq times V_ whete, i order to take account ofthe obsiguctions in city areas, is defined from a general obstruction level. Smaller exponents g are used‘) than those presented in Table 8, which are consistent with a reference height of 10m‘), The method of estimating wind loads herein and in the Code should therefore not be confused. Table 8 Approximate ratios of gust to mean wind speed for different averaging periods V4/P for ground roughness, Zy Averaging Z, = 0.003 0.03 03 203 period, 0.2 on 020 0.25 3s 15 7 19 2a 158 1s Ls 16 18 60s 12 13 1 1s ‘The gustiness of the wind was initially defined by Davenport and was later modified by Harris) in terms of a power spectrum of wind speeds of component frequencies, The greater intensity of spectral ordinates are in the lower frequency range. Spectral methods form the basis of the following analysis of structural response. ‘The forces exerted are determjned by a drag or force coefficient, Cr, and representative wind speed, ¥, such that pressure (in N/m*) = 0.613 Cr¥? (Vin m/s). In most cases, large, stiff structures do ‘not respond dynamically to wind gustiness, and their induced forces can be considered to be ‘quasi- static’. Therefore, the wind speed which acts on the surface should only reflect the spatial average of ‘the wind. For small structures or parts of a surface, the 3-s gust speed may be representative, whereas, for larger surfaces, a 15-s gust wind speed reflects the time necessary to generate the maximum force over a surface, Cladding forces resulting from positive or negative pressure may be locally very high, particularly where the shape of the structure of the incidence of the wind causes turbulent eddies at the corners of the building. This is reflected in the use of local negative pressure coefficients considerably higher (2.0) than the average value of about Cr = 1.2 (+0.8 windward, ~0.4 leeward), used in calculating ‘the overall force actions on tall buildings. The wind flow around a typical tall building is shown in Figure 28(a). The force coefficients for rectangular buildings? of different proportions are given in Figure 28(b). Tall or flexible structures respond dynamically to some extent, Most methods for estimating the structural response are based on spectral approaches, where the structural admittance, Z, is defined as 1 function of the natural frequency of the structure, f, and a damping ratio, It is rare for the second mode of bending to be important for shear Wall structures, but possible torsional modes should not be overlooked. This is described in principle in Seetion 4.2.3 The overall response may thus be expressed in terms of a mean component and broad-band and. narrow-band responses, The narrow-band term represents the vibration at the natural frequency of the structure. The broad-band term is the component at the background frequencies of the wind, and itis largely quasf-static. Both broad- and narrow-band components are evaluated by spectral ‘methods in terms of the root-mean-square (rms) amplitude of vibration. The peak value over the design storm period (1 h) is given by a factor, g,, which is 3.5 to 4.0 times this rms value, ‘The dynamic magnification of force resulting from the flexibility of the structure is therefore the total response divided by the quasi-static response, which is the sum of the mean and broad- band components. a099 109 140 150 Negative pressure 6.0_000085 Joss }105 190, 145 170 )0 saf_} is Sagan — tal 30 High negative \ a pressate al formers aa er : igh zy relates 3 imeey z {2} Wind tow around bilan & ) : 305 [ 0m 04 06 08 10 7 30 40 Breadth depth ratio Figure 28 Wind forces on rectangular building {) Force coetcient,C; 43.3 Mathematical The method used for evaluating the structural esponse of tll, rectangular shape bulldings is that of treatment of structural Wyatt". Although the method is general, certain approximations can be made from uniform mass Reaparas structures with constant section, typical of most tll buildings, The nafrow- and broad-band responses are determined separately. The rms total force (or stress), on (Q), divided by the mean force at, the base of the structure, 0, is given for the narrow-band component by on(@) _ 034 [a (on\/s.927n\ os 47 Q- Gatws e(¢ rasa) asa “ where & is the damping ratio, fais the natural frequency of the building, Ty isthe timescale of the wind at the height ofthe stricture, H (Figure 29), Ly isthe length scale of the wind (=Pig/(8.9fq)), Vix is the mean hourly wind speed at height, H, o}4/V represents the intensity of turbulence at this height (Figure 29), and Ag represents the exposed area of the structure to the wind ‘This ostensibly fearsome equation can be simplified for design use. The admittances, J, andJz,can be taken to be unity (actually 0.9 to 0.95) for reasonably large buildings. The factor Ky, representing, ‘mass and mode shape variation, is also roughly unity. The factors Ty, Lyy and oy4/P xq are a function of the wind structure (and henge of ground roughness, Z9). The ratio of the rms peak displacement divided by the mean displacement o(Y)/¥ is also further affected by the variation of wind and structural properties with height, but asa first approximation may be taken as equal to 0(Q)/Q, as given by the above formula, with a possible error of up to 20%. ‘The broad-band component may be determined from Figure 30, and the total induced force, Q, relative to the mean force, J, in any element at the base of the structure is given by the vector sum of these responses. 2-0 [i+ [een QMO? *e0uioI0F | (48) ‘The multipler,g), for the narrow-band response may be taken to be 4.0, and g7 is related to the effective height (if, = 2/3H) by: 81 = 4.1 ~ 0.25 logiolle 49) Inherent in these formulae is that the mode shape of the structure is basically linear, which is reasonably accurate for shear wall structures. The ratio Q/ may be greater towards the top of the building, The mean value, G, is proportional to the square of the mean wind speed and therefore falls with increasing Zo. [tis usually found that, for structures which exhibit litte narrow-band response, the ‘overall forces on the structure can be conservatively calculated using the 15-s gust wind speed. (S2 values in Code'*?)), For most shear wall structures, the narrow-band component of force (and hence displacement) contributes about 15 to 30% of the total in city centre environments, and 10 to 20% in other urban environments,Figure 29 Wind turbulence parameters for ‘dynamic analysis CIRIA Report 102 ‘The curves in Figures 29 and 30 are presented for Zp values of 0.003, 0.03 and 0.3 only. In inner city areas, the dynamic response may be affected by wind buffeting between buildings. However, the ‘overall forces on the building may be calculated with reasonable accuracy, using Z = 0.3, although ‘the proportion of the narrow-band response increases as the relative height of the surrounding buildings increases. This effect can only be predicted accurately by wind-tunnel testing. In more complicated cases, itis recommended that the full method proposed by Wyatt(“*? should be used. Nevertheless, the above formulae give a straightforward method for calculating the structural response with reasonable accuracy. A similar method is given in the Canadian Code™”) which gives comparable results. 200: 1184 1504 14 50m/s 100: 184 Height above ground, H(m) 4}, a ee om 0% aul ‘, 0) _ Intensity ot urbutnes 0% Time scale, 7, (broken lines} 5 0 8 2 % 4sFigure 30 wind response NSS SS o A NI 3 < = 2.203m In each case:- Line A= vertical Line structure B= width -0-2 xheight C=width -05x height D = width equal to height based on linear made shape 0 20 Height of structure, A (m) 50 100 200 400 CIRIA Report 102434 Example calculation of structural response 435 Torsional response of structure from wind 4.4.1. General cri 44.2 Criteria for wind-induced motion CIRIA Report 102 Shear wall building on outskirts of large town Data: 60 m high, 24 m wide natural period 1.2 s (0.83 Hz) total damping 2% (structural and aerodynamic) Winds 2970.3; TH = 15.5 6; Mio 0 m/s 0.20; V5/P = 1.9; (Table 8) oy/ 19 (from Figure 29) ‘Therefore Myx = (60/10) ° x 40/1.9 = 30.1 m/s Ly = 30.1 /(8.9 x0.83)= 4.1 Narrow-band response: os ont) 0.34 " (2344) @ (oss x 15.5" for *°19*\Gox24 oe Broadband response (Fine 30) 2B) = 036 and g2 @ Tota force» O[1 + Ja oxoa0F v.65 x00" |= 2370 The ductastig component of force (ordlcement the natural quency ofthe satus thas 4.0 010/237» Tio he total (geakemean). Ths mean fore onthe auctare, 0, maybe calculated from the above mean wind speed and expongat, This method may be expected to produce slightly higher forces than the Sz approach in the Code™), 65 Because of possible cross wind response, of any eccentric mass or stifness, the structure may respond in.a torsional a5 well as flexural manner. Tall, square or round structures may experience cross- Wind motions of the same order as the in-wind motion, resulting in an elliptical orbit of vibration, Similarly, the shape of the building can induce further lateral motion as a result of asymmetric shedding of eddies. Calculation of these effects is beyond the scope of this Report. Itis usvally found that those effects contribute to an increase in the narrow-band response. An empirical method for calculating the cross-wind response of tall buildings is given in the Canadian Code'*”?. Dowrick'*?? suggests that, even in symmetrical buildings, a minimum torsional moment of 2.5% of the lateral force times the building width should be considered in design. 4.4 HUMAN RESPONSE TO MOTION ‘The level of adverse comment from the occupants of a building to vibration is dependent on the return periad and the time over which motion ofa particular intensity if sustained for each ‘occurrence’, The level of tolerance to vibration is a function of the activities being performed and of the readiness of the occupants to accept the significance of the vibration. In a hospital for example, the need to carry out delicate operations requires that vibration levels should be minimal”) The threshold of perception to vibration‘*") is shown in Figure 30. The ordinate of this illustration is in terms of rms acceleration which is defined as the average of a sinusoidal wave form Ge, peak/V2). The abscissa is the natural frequency, fn. These limiting accelerations are extremely: small, Increasing the level of vibration results first in adverse comment, then annoyance, leading to alarm. Storm periods are usually assumed to be fully developed for longer than 10 min. During a storm, certain extreme motions are experienced, One single action may cause alarm, but itis the general Jevel of motion over the period which is important. ‘A certain proportion of people (roughly 2%) is generally receptive to, and complains about, even very small vibrations. A ggasopable serviceability criterion may be that a further 10% (i.e. 12% total) may comment adversely"), These limits are shown in Figure 31 in terms of the average rms acceleration for a 1-in-S-year storm. In wind analysis, the rms value of the narrow-band response at the natural frequency of the structure is, in fact, the rims of the response record in time, and ‘over the storm period an extreme value of g, times this rms is experienced. For compatibility the ‘ordinate of Figure 31 is multiplied by g to obtain the design peak acceleration throughout the storm period. 47Figure 31 Curves of perception and satistactory ‘magnitudes of horizontal structural motion with respect to human response 443 Example calculation of human response to vibration 48 Aidance stinary 03 Unt strc - tras personel , 7 iuilding occupants compan) 006) le Ze 0-05} PN] -- FA 4- 2%e complaint f= = a te 06 eg pcetin 0-02} = wi 1 é Perception level for E 000s i [Jeewr] Peak vale 3 [ FY 3 Pero id Aneage rns wor Wea Gy 1a Perabo Frequency (Hz) The peak acceleration may therefore be 3 to 4 times the rms level of Figure 31. Deflections may be evaluated by dividing by the square of the angular frequency (27 frequency). In most cases, it may be considered that the line in Figure 31 corresponding to 12% adverge comment for Lin-Syear wind speed is an acceptable serviceability criterion. In the Canadian Code™”), a limit on peak acceleration of 2 to 3% of gravity for a 1-in-10-year recurrence wind is made, which is broadly equivalent to an average rms acceleration of 0.5% of gravity for the normal range of building frequencies. However, in certain structures (e.g, residential blocks), a lower level of wind-induced vibration may be required. ‘This vibration is greatest only in the upper third of the building. Torsional and translational motions should be combined to give an equivalent translational motion on plan. Because of the visual perception of twisting, it may be necessary to adopt more severe criteria where this is the dominant motion. Consider a 60-m high shear wall office building with a fundamental natural period of vibration of 1.2 (frequency 0.83 Hz) and design wind deflection of 60 mm. The narrow-band component of this deflection is estimated as 20% for this structure (ie. 12 mm quasi-static to peak), CIRIA Report 102From Figure 31, the limiting serviceability criterion for occupancy comfort in the upper storeys (taken as approximately 12% complaint level for I-in-S-year recurrence wind) is 0.04 m/s* average ‘ms acceleration. Dividing by the square of the angular frequency, the permissible rms deflection, becomes 40/(2r x 0.83)? = 1.5 mm, The peak value is normally about 4 times this rms value (see Section 4.4.2). Therefore the peak resonant deflection for the S-year recurrence wind should be less than 1.5 x4 = 6.0 mm. ‘The usual design wind speed is the 1-in-50O-year value, for which the ratio of the mean (and gust) ‘wind speed to the 1-in-S-year recurrence wind is of the order of 1.3. Although mean forces (hence deflections) vary as the square of the mean wind speed, the narrow-band component tends to increase relative to the mean and broad-band components asthe wind speed increases. Therefore the equivalent narrow-band deflection based on the 5-yearly wind speed can be conservatively taken as 12/1.3* 7.0 mm. This is about 15% greater than the permissible deflection. This simply calculation is tentative, ‘but it shows that human comfort criteria can be important, In many exposed sites, it may be considered uneconomic to adopt such a severe limit on the comfort of the occupants to motion. In addition, the above calculation overestimates the structural response at relatively frequent wind speeds. 5. Elasto - plastic and seismic behaviour 5.1.1. Planar Walls CRIA Report 102 ‘This Section covers the behaviour of walls beyond the elastic range. The elastic design of walls for ‘compression and overturning moment was presented in Section 3.2, and the ultimate strength of the extreme fibres of the wall checked by conventional column design. In the post-elastic range, re- distribution of forces occurs, both internally and between walls. In pierced shear walls this redistri- bution can occur by lintel yielding, before the ultimate strength of the wall elements is attained. Such yielding and inherent ductility is important in seismic design, 5.1 ULTIMATE STRENGTH OF WALLS IN COMPRESSION AND BENDING ‘The resistance of walls to overturning can be determined from conventional plastic analysis of the wall cross-section. Collapse occurs when the plastic stress blocks of Figure 7(c) (page 19) are reaches. This overestimates the usable strength, because of the large strains required o develop the full capacity of the reinforcement. The compressive resistance of the concrete) is N. (= 0.4 feytL) and that of the total steel area, 4s, is N,' (= 0.72 fy). The coefficient of 0.4 (rather than 0.45) takes account of the concrete stress block in bending, The strength of the reinforcement in tension is N (= 0.87 fy). The neutral axis depth, xp, in the presence of an axial load, N, is siven by equilibrium of concrete and steel stress blocks a8 XplL = (Ng +N) | (Ny + Ne) «s0) where Ny = Ne +N, op ‘The maximum moment which can be transferred is therefore MSLI2(N + Ny) Ny ND | (Ny +e) (2) ‘This simple formula may also be used for N in tension (N +N, > 0). Where the slenderness of the wall is greater than 12, its ultimate strength is limited by destabilising effects. The equivalent ultimate compressive strength of the wall should be reassessed for input into the above equations. Because of the uncertain effects of instability, elastic design should be employed for relatively slender ‘walls, It is assumed that a sufficient reserve exists against shear or foundation failure. A typical ultimate moment-axial load diagram is shown in Figure 32 for various levels of reinforce- ‘ment. This idealised stress block method is attractive because of its simplicity. In detailed design, the section strength should be checked by the method of Section 5.1.3. Where reinforcement is con- ‘centrated at the edges of the wall, the column design charts of CP1i0 may be used.5.1.2 Channel-shaped walls 5.1.3 General plastic analysis of an irregular cross-section Figure 32 Unimate moment- ‘axial force curves for plane and channel walls 50 ‘The above plastic analysis may be extended to the analysis of channel seetion walls. Ifthe above ‘parameters, Ve,.N, and N', refer to the web of the wall, an additional series of terms Ner, Ny, ‘Ng, apply to each of the flanges of the channel. The neutral axis depth, xp, therefore becomes pl = (N+ Ng + Neg ~ Nop) (Ny +N) (53) where Nye = Nort Wu and xp am — sm = Wall section under uniform lateral leading be oat eae a Im Sm wy _ Lateral load 10 9," Toad tor nial yi aff aft . os x/H tor 9 = max. z ° aft to 15 win Uneracked stiffness 1 Elastic Limit in intel 2 80% of lintels yielded sage )stage tae z 3 All intels yielded 3 4 Flexural capacity 3 Lateral of wall exceeded = ductility i 3 — Ts ~ 3 won w } at Rotational ductility of intl, ¢/6, Lateral deflection of top of walt i} (b) Figure 37 Behaviour of shear wall up to failure sa CIRIA Report 1025.2.3 Modified elastic methods 5.2.4 Step elasto- plastic analysis 5.2.8 Ductility demand 5.3.1. General background CURIA Report 102, In post-clastic conditions, cracking and structural degradation rednce the structural properties below those for elastic analysis. It is possible to use elastic grillage methods to predict the forces developed. in tie structure if those elements which are cracked are attributed reduced stiffness. One way of cartying this out is to assume a certain zone of plasticity in the wall ta given loading and using the modified properties for this region, to recalculate the forces in the structure. Paulay'™? suggests reduced stiffnesses (inertia J, and atea A.) of the walls and lintels for cases of severe elasto-plastic load cycling, such as experienced during extreme seismic events. These are typically’ Wallin tension and flexure Te" 0.5 Io, Ae = 0.5 Ao ‘Wall in compression and flexure Te= 0.8 Io, Ag =A, Coupling beam- conventional reinforcement I_=0.2 Io Coupling beem- diagonal reinforcement [y= 04 Ty For smaller amplitudes of vibration resulting from wind excitation or less severe seismic events, itis more realistic to use the gross area A, and inertia J, of the walls, and to calculate cracked section properties of the lintels using the actual amount of reinforcement, as in Section 3.3.3, page 29. An iterative procedure is requited to predict the internal forces, but itis usually found that only one (or possibly two) iterations are required. The overall force distribution is relatively insensitive to small changes in any of these properties. ‘A number of methods have been put forward to predict the elasto-plastic behaviour of shear walls Most use the continuous connection technique with step-wise modification of the lintel stiffnesses ‘with increasing deformation. These methods have been specifically developed for earthquake analysis aad they may be combined with sophisticated timestep dynamic methods, A detailed description of these pgthods is beyond the scope of this Report. Reference to papers by Nayoor and Coull Paulay'**? is recommended, One of the principal requirements of elasto-plastic design is to be able to predict the ductility of the lintel beams during the elasto-plastic load cycling. This is shown diagrammatically in Figure 37, where the load-deflection curve is plotted throughout the full history of deformation up to wall or foundation failure, In order to develop the full plastic resistance of all the lintels, (when equally reinforced), the required deformation of the most highly stressed lintels may be 8 to 10 times the deformation required to cause yield, as defined by Equation (61). At 50% greater loading than that necessary to cae fist yedin the ntl, the dutty demands pat 4 to 5, To achieves ater or sway ductility of the building of 4 as specified by some codes(™”, the required ductility demand of the lintels may be of the order of 12. There should be sufficient strength reserve in the wall and foundations to generate this ductility (see Section 5.1.3, page 50), The importance of detailing is discussed in Section 5.4.2, If the lintels are reinforced in proportion to the shear forces which they attract, the ductility demand is theoretically unity as all the lintels ‘would reach their ultimate strength simultaneously, The sway deformation then increases more rapidly with increasing load than the case where all the lintels are equally reinforesd n practice, tis usual to adopt a standard detailing procedure forall lintels. In such cases, Paulay™? states that the reinforcement provided in a band may be 20% less than that for the peak moment without affecting the elastic behaviour of the wall, Inherent in this analysis is that premature shear failure of the lintels oF the walls does not occur. ‘The analysis presented so far relates to pierced shear walls under uniform lateral loading. In squat or short walls, the failyze mode is one of shear rather than flexure, and the structural behaviour is indicated in Figure 38). These walls do not possess significant ductility. Slender or stepped walls, cor walls with variable openings, also present uncertain elasto-plastic characteristics. 5.3 SEISMIC DESIGN METHODS Energy release from seismic activity may take a number of forms, ranging from a single shock with very high accelerations or up to 30 cycles of strong ground motion, resulting in sequential degradation of the structure and soil liquefaction. General scales have been developed to define the intensity magnitude of seismic activity. The most popular are the podified Mercalli and the Ross-Forel sales (both intensity) and the Richter magnitude scale), The Richter-scale defines the energy release during an earthquake on a logarithmic scale, The approximate magnitude of these scales is presented in Table 9 355.3.2. Treatment of seismic forces Figure 38 Shear behaviour of low-rise wall 56 ‘The seismic forces of greatest effect are generally those in the horizontal direction. However, vertical excitation can lead to reduced shear resistance or local crushing. Three basic methods are employed to deal with seismic actions. For low- or medium-rise buildings, most codes permit these forces to be treated as equivalent static lateral forces. A second method is to obtain the response of the structure by modal super- Position, using response spectrum analysis, The most detailed method for analysing the behaviour of special structures is that of time-step integration for specific earthquake records Response spectrum methods are reviewed in Section 4.2.3. A typical design seismic response spectrum of a single mass system in terms of acceleration, velocity, or displacement for various levels ‘of damping is shown in Figure 39. This is smoothed and scaled to a ground acceleration of 20% of aravity (for a structure of zero period). The structural response to smaller ground accelerations may be estimated by scaling these curves in proportion to this acceleration. The natural period of the structure is along the horizontal axis, ‘The earthquake record used to generate this spectrum should be typical of the geological conditions and records in the region under consideration, Table 9 Approximate description of earthquake intensities Modified Richter Approximate | Effect Mercalli Seale Scale acceleration 1 3 a Fett slightly 2 0.001 - 0.003 | Felt indoors 3 0.003 - 0.005 | Some cracking 4 5 0.005 -0.01g | Some movement. ‘Alarm 5 6 0.01 -0.025¢ | Some damage. Chimneys fall 6 0.025 — 0.05 | Panels deformed. Some buildings collapse 7 7 0.05 0.10 Considerable damage, Frames out of plumb. Masonry buildings collapse 8 0.10 - 0.258 Most frame structures seriously damaged. Landslides 9 8 0.25 - 0.58 Few structures survive Force in reinforcement Shear force Nt Sof cA 7 NS iS Nn S ‘rack pattern SX, Crack patt53.3 Code Formulae for the assessment of base shear from seismic events take the form of the empirical treatment of equation below, This shear force isto be proportioned a Iateral force atthe top of the building (Commonly 15%), and a trangulary distributed load increasing with height. The forma given inthe ae Gioia Cours Q=ziKesw (63) where C is the structural flexibility factor (calculated from C= (15[ 7°)", and T is the natural period ofthe building as determined from Table 4 or from dynamic analysis (se Section 4.2.1, page 40). The value K reflects the ductility and energy reserve of the structure. For box or shear wall structures, K = 1.33, reducing to 0.8 if ductile frames can be introduced in the structure to resist 25% of the applied lateral forces. Fis an importance factor (usually unity). The zone factor, Z, anges from 0 to 1, and it reflects the severity of the seismic event. S is related to the foundation flexibility, and may be taken as unity for very stiff soils, and 1.5 for more compressible soils, such that CS<6.14. W is the total dead weight of the building. A limit on lateral deflection of H/200 is specified, A formula, but with different constants to Equation (63), is given in the Canadian Building Code'?). This shear is usually applied with a nominal eccentricity of 5% of the building width, Further torsional excitation should be minimised by careful choice of structural form to minimise plan eccentricity of mass and stiffness (see Section 4.1.2, page 40). 5.4 DESIGN AND DETAILING FOR ELASTO-PLASTIC BEHAVIOUR 5.4.1. Structural One train of thought in design is for a structure to be as flexible as possible to minimise the effect behaviour in seismic _of high frequency excitation. Unfortunately, although damage to the structure may be superficial, action the non-structural elements and services may be seriously distorted. The building may also respond badly to wind excitation, Another approach is to provide avery stiff but ductile structure which can withstand strong, high frequency excitation by eracking in certain zones which can be repaired. In order to achieve adequate ductility (and hence energy absorption), some codes”) require that the structure should be able to exhibit a certain minimum sway ductility beyond its design point. 00] 250) 200) Spectral velocity (mm/s) yx Figure 39 vy Design response sn 002 0-04 005 01 02 «04-060810 20 60 60 60700 Binion feel seismic loading te: original data in inch (CURIA Report 102 ST5.4.2 Detailing requirements 58 ‘The hierarchy of ductility is that compression and shear failure of concrete should be avoided in favour of yielding of reinforcement. Foundation failure should not occur. In spite of the load cycling, members which are severely deformed should continue to absorb energy. This imposes constraints on the detailing of the reinforcement both to encourage yielding and to confine the concrete in compression by use of shear links. ‘The lintel beams between walls act as good points to undergo elasto-plastic deformation, because ‘the overall structural integrity of the building is not badly impaired during such action. In some very important buildings, it may be necessary to limit the degree of damage either by designing the walls, clastically for the maximrum probable imposed forces, ot by permitting yielding in well defined plastic ‘hinge zone There are certain geometrical proportions of structure which behave better in seismic action than others. Paulay and Williams(™*? suggest a categorisation factor, K, for use in calculating seismic forces, based on the proportion of lintel coupling, Ti/Mo, #8 defined in Section 3.3 (page 22). For plain squat walls with aspect ratio (#/D) less than 2, K = 1.6, and for multiple parallel walls with HID > 2, K = 1.0, increasing to 1.2 for single walls. For pierced walls with TI/My = 0.67, K = 0.8, and for Ti/Mg = 0.33, K = 1.0, In general, structures with a low fundamental period (<0.6s) are likely to be subjected to a higher ductility demand, Detailing criteria for elasto-plastic cycling may be divided into those of flexure, compression, and shear, which influence the distribution and sizing of the reinforcement, particulary at the extremit fof the walls and at the junctions between the lintels and the walls, Another factor is that of slippage at construction joints. These requirements are presented in Appendix A of the American Concrete Institute Code’). The following sections summarise the criteria adopted by this and other sources of, dateronet $5861 60083 Flexure of lintels In order to achieve uniform yielding of the lintels along their length under double curvature bending, ‘beams are often detailed with diagonal cross reinforcement in addition to that reinforcement required to resist local loads. Shallow lintels may be reinforced in a conventional manner. Their relative a aa dleplacement curve 172505 7 eb we for various joints Oisplacement (mm) CIRIA Report 102Requirements of CP110 for shear at joints ‘The shear resistance of various concrete surfaces is defined in simple terms in CP110) . For joints with ordinary surface treatments or for dry pack of grouted surfaces, no reinforcement need be provided if the shear stress is less than 0.23 N/mm?. This increases to 0.45 N/mm? if the surface is Prepared by brushing to remove the latence. In addition, the shear stress, calculated on the root area of a castellated joint, should be less than 1.3 N/mm? ‘Where clamping reinforcement is provided across the joint to resist the entire shear force, the shear strength is given by Pr = 0.6 x 0.87 fy Ay tand (68) The term tan @ defines the friction coefficient of the concrete surfaces. Values range from 0.7 for untreated concrete to 1.7 for castellated joints with in-situ strips of concrete (see Figure 43, page 61). 6.2 BEHAVIOUR OF INFILL PANELS TO FRAMES {In traditional framed structures the presence of infils of masonry or concrete can greatly increase the stiffness of the building to side sway. In low-rise buildings, such infills are often assumed to resist all lateral loading, but in high-rise buildings this is usually considered to be unreliable, and the beneficial effect of the infills is often limited to sway reduction only. A tentative means of utilising the strength and stiffness of infills i to design the frame alone to resist lateral loading, using load factors appropriate to the survival limit state (see Table 3, page 15). ‘The inflls should then provide the remaining factor of safety for normal ultimate load design. If infills are to be utilised, they should have strength commensurate with their stiffness as they undoubtably attract considerable loading in their own plane. If such loading isto be avoided, ‘movement joints should be provided between the perimeter of the panel and the bounding frame, 6.2.1 Reinforced {In order to participate in the structural action, the connections between the panel and the frame ‘concrete panels should be both sufficiently stiff and strong. Any misfit accentuates the sway deflection of the building (Figure 48). Long-term shrinkage or thermal movements amounting to only 1 to 2 mm. over the panel may be significant in increasing sway. In cases where a tight fit within the frame is required, the need for construction tolerances should not be overlooked in design. Conerete panels can be cast within the panel or fixed at their corners by steel plates welded or fastened to the frame by brackets with friction grip bolts, Steel or reinforced concrete framed buildings cen be used with such panels, although creep shortening of concrete columns may impose ‘additional stresses on the connections. The panels are relatively much stiffer than the frame, and therefore itis not unreasonable to assume that the panels attract all the lateral loading. Local shear stresses around the frame-panel connection should be checked, and the pane] reinforcement should be detailed to accommodate the bursting forces, The panel may often be seinforced diagonally as a column. Because of the tension compression action of the diagonal struts, instability of the panel is unlikely if the panel diagonal is less than 30 x thickness. Any eccentricity Of the panel to the centresine of the frame should be included in the panel strength analysis. Shear stresses should also be within code limits") Sheat force ‘Cracking oti Figure 48 6421 KN m. For minimum compression x Xe Mamas = 0.10 (Figure 32) ‘Mg max. = 0.10 x 5 x 20327 = 10 163 KN m> 6421 kN m \ Report 102 15ULTIMATE STRENGTH OF LINTELS Peak ultimate moment = 1.4 x 184 = 258 kN m Allowing 20% reduction, My = 258 X0.8 = 206 kN m Moment of resistance (Three ¥25 bars top and bottom) p= 1.19% and x= 200 mm ‘Ma max = 0.87 425 x 3 x 491 x 10° (548 ~ 100) = 244 KN m>206 kNim Gu = 244 x 2/(2 x3) = 81.3 kN/m height SERVICEABILITY STRESS LIMITS IN WALLS ‘The stresses in the concrete and reinforcement at working load are calculated from elastic analysis. of the wall cross-section as in Section 3.2 page 19. Max. compression, N'= 2521 + 1800 + 1620 + 720 = 6661 kN and e/L = 4587 / (5 x 6661)= 0.14 Min, compression, N= —2521 + 1800 + 1620= 899 KN and e/L = 4587 /(S x 899) = 1,02 For e/L. = 0.14, Nmax, = 1.8 No (Figure 8, page 21) where No = N/L Nemax, ™ 1.8 X6661/5 = 2398 kN/m length of wall ‘Max. stress in concrete for r= 0.02, and m = 8 (Section 3.2.2 page 19) is 0¢ = 2398 x 10? / (1.16 x 225 x10) = 9.2 N/mm* Fore/L = 1.02, solve Equation (3), page 19 for neutral axis depth, x Try x/L = 0.35, with r= 0.02, and m= 8 035? — 3 x 0.35? (0,5 ~ 1.02) +6 x 0.35 x 1.02 x 0.16 — 0.16 (3 x 1.02 +0.5) i.e. 0.043 + 0,191 + 0.343 - 0.56320 From Equation (4), max. force on section is: Noa 16 ao No” (5x035 +016 (105/038) Nur * 899 x 10/5 = 1960 EN eg of wa Max. stress in concrete, 6, = 1960 x 10° (1.16 x 225 x 10°) = 7.5 N/mm? ‘Max, stress in reinforcement, , = 7.5 x 8 x 0,65/0.35 = 111 N/mm? ee rere Inca h meas a a aseciaes vee ereaa aes SERVICEABILITY STRESSES IN LINTELS tons nine woe Jad 1040 Netra oxi depth (Equation (2), pee 29) for mp = 0.0119 x8 = 0036 ‘Tq (0.35? [3 + 0.096 x 0,657) 225 x 550° = 2.05 x 10° mm* 84 x 8 x $50 x 0.65/2.05 x 107 = 257 N/mm? 70 N/mm?) Stress in reinforcement 0, This is less than 0.87f, CIRTA Report 102CHECK CRACK WIDTHS ‘Tho crack widths at the lintel-wall junction are likely to be the greatest. The calculation of crack widths is presented in CP 110, Clause A3. It may be shown that for bar spacings of less than 75 mm in the lintels, the crack widths are of the order of 0.3 mm for the above reinforcement stress. similarly for bars spaced at 150 mm or less, the crack widths in the tensile faces of the walls will be [ess than 0.3 mm, ‘These are considered acceptable because of the momentary nature of the peak response and the ow probability of the extreme loading, SWAY DEFLECTION OF WALLS From Equation (78), page 79, the peak deflection is wit 1 BL Bhs a\i Beams § 27 Gant alt ) (am? For Sti/a? = 0.00184 x 7/0.015 = 0.86 ve (1-086) , 9.86) 30x 10° x2x 2.34 8 * 14 = 32.3 mm (Height/1860) ‘This is considered acceptable with respect to human response (sce Section 4.4.3, page 48). ESTIMATE OVERALL FACTOR OF SAFETY ‘As the lintels begin to yield, calculate the available factor of safety before the ultimate strength of the walls are reached allowing for 30% redistribution of moment between walls Loud factor corresponding to ultimate moment in the most-stressed lintel is 2 euste = 244/206= 1.18 Peak lintel force occurs at x = 0.281 from elastic analysis (Figure 8, page 22) Partial plastic analysis (Section 5.2 page 52) ‘Assume yielded zone up to 3 =0.7H, with x1 © 0 From Equation (58) page $3, equivalent loading is w . 2+74? x07 =034 Gu 0.00184 x60? x 0.65? x0.7 w = 813 x034= 27.6 kNim Overall load factor Ay = 27.6/14.9 = 1.85 Axial force in walls (Equation 62 , page $4): Ty = 81.3 x 60 x 1.7/2 = 4146 kN Moment in walls My = Mz = (1.85 x 26 820 ~ 4146 x 7)/2= 10 298 kN m ‘The ultimate strength of the walls may be rechecked as in Section 5.1 (page 49). A 10% increase in ‘moment is to be made to account for the eccentricity of axial load (P-5 effect) It may be shown that the ultimate strength of the wall in tension is reached at this overall load factor. It remains to check the available ductility in the lintels RIA Report 102 n8 DEFORMATION CAPACITY OF LINTELS ‘The band of lintels which are deformed plastically are assumed to be equally reinforced. The most- deformed lintel occurs at level xq given by Equation (59), page 53. 4 0.015 Hw ~ 0.00184 x 60x 034 2m = 1-044 4 —04404x07'= 04H Rotational ductility (Equation (61), page 54) Parameter 0.40 4 = onossxasexca?[or x0472—oac.rx042 047] 0 = 3.20) Tis teste ont of oman een te int ei ati otha fina yield, in order to generate the plastic zone in the lintels for R, = 1.85. This is considered acceptable, because of the relatively low percentage of reinforcement in the lintels. ‘The shear strengths of the walls are to be assessed in a conventional manner, taking into account the compression on the walls resulting from selfweight, and the action of the horizontal reinforce- ment as shear-stirrups. ‘These calculations show that, for the purposes of a Scheme Design, the shear wall strength and in- service performance is satisfactory. The value of aff which has been used takes into account the lintel to wall flexibility, but it neglects other effects. The structural sensitivity should be assessed for, say, a 30% reduction in a, the effect of which is to increase the over-turning moment in the walls and to reduce the forces inthe lintels. CIRIA Report 102Appendix 2. Formulae for pierced shear walls CIRIA Report 102 The following are general solutions derived from the method of Section 3.3, page 23, for the elastic behaviour of a pierced shear wall. A lateral force, P, is applied at level, xi, and the shear flow in the lintels, the axial foree in the walls, and the lateral deflection are calculated at level, x. The term in brackets < > is included only when positive. Otherwise it is taken as zero. SHEAR FLOW IN LINTELS 1 @ cosh a | oo) foo otc a~ cotati») AXIAL FORCE IN WALLS = fe ‘sinh o(H — x)) cosh. sinh @ (H ~ x) r+5 1) cosh ax — sinh a (Hf ~ x sth sok n> acs >| om LATERAL DEFLECTION . “zt (- Eon = teste is as defined on page 79, The geometrical parameters are siven in Figure 25, page 37, a= -20) go — Se 2 sia -) _ 7 1 ‘ay —*) + 1 finn yet + si —x) yx; — 1) - si =x rag tt rao 2) where 7? avy hed 'D(D + 28) Iq(D + 25)? AWE a 2 O° Fea awe = position of shear centre of channel = 3D=b-08 430 -- +L) = St. Venant torsion constant = GP +D-b- 9/3 w End warping constant 2 > manos [ge] = Inertia of channel = Inertia of coupling beam 80 CIRIA Report 10