You are to test the claim by a mineral water bottle manufacturer that its bottles contain an

average of 1000 ml (1 litre). A random sample of n = 12n=12 bottles resulted in the measurements
(in ml): 992, 1002, 1000, 1001, 998, 999, 1000, 995, 1003, 1001, 997 and 997.

It is assumed that the true variance of water in all bottles is \sigma^2 = 1.5σ2=1.5, and that the
amount of water in bottles is normally distributed.

Test the manufacturer's claim at the 1% significance level (you may use Excel to calculate the p-
value). Also, briefly comment on what the hypothesis test result means about the manufacturer's
claim, and if an error might have occurred which type of error it would be.

-------------------------------------------------------------------------------------------------------------------------------------

H0: 𝑥̅ = µ = 1000 ml (Mineral water bottles contain 1000ml (1 litre) like

company claimed)

H1: 𝑥̅ ≠ µ (Mineral water bottles do not contain 1000ml (1 litre) like company
clamed)

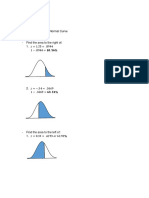
µ = 1000 Significance Level (α) : 0.01 σ2 = 1.5

(992+1002+1000+1001+998+999+1000+995+1003+1001+997+997)
𝑥̅ = = 998.75 ; µ ≠ 𝑥̅
12

998.75−1000
Z= = -3.53553… = estimated -3.54
√1.5÷12

P-value of Z = -3.54 = .00022 = estimated 0.0002 < α 0.01,

Reject H0

Which means mineral water bottles do not contain 1000ml (1 litre) like
company claimed.

It is possible to miscalculate and comes up with Type II Error (Not rejecting H0

then turns out that H0 is false.)