1

Biot-Savart's Law

Earth's magnetic field power station turbines magnetic hard disk drive

Magnetic fields are weak natural phenomenons which are now heavily exploited in man-
made technology. This has had a huge impact on everyday life, from electric power to
computer storage. Future developments such as fusion power crucially depend on the ability
to construct powerful magnetic fields with particular shapes.

Whereas electric fields arise due to stationary charges, magnetic fields arise due to moving
charges, or currents. Key breakthroughs in the understanding of magnetic fields were
Ampere's Law and Biot Savart's Law, which enable one to calculate the magnetic field due to
particular arrangements of current.

Objectives

1. Measure the magnetic field due to current carrying conductors including loops.

2. Measure the axial magnetic field of an air solenoid.

3. Measure the radial and tangential magnetic field of a coil.

4. Measure the axial magnetic field of a pair of Helmholtz coils.

Version 1.1, 01/10/07

 2

Key Safety

This experiment involves the generation of artificial magnetic fields using current from a
power supply. Although large currents are used, up to 16A, these should not be dangerous
because the voltages involved are very low. Nevertheless, the conductors carrying these
currents may overheat. The black plastic connectors also get hot. You must take care not to
touch exposed metal which is carrying current. Note that the metal stands and optical bench
will not be carrying current provided you follow the instructions properly.

Apparatus

various connecting cables air solenoid with variable length

axial B-probe stand for air solenoid
Teslameter holder for conductors
pair of Helmholtz coils assorted conductors
high current power supply stand base with small optical bench

Key apparatus

All observations made in this experiment rely on an axial B-probe. This measures the
strength of the magnetic field component which is in the direction of the probe axis. This
means you must be careful to have the probe in the correct orientation relative to the
apparatus which is generating the magnetic field. In addition, the probe axis is fragile and for
this reason the probe must always be mounted on the optical bench with its axis parallel to
the optical bench axis. The sole exception to this is when measuring the magnetic field of the
air solenoid. For that measurement only, the probe should be transferred to a stand base.
Finally, the measurements will be affected by background magnetic fields. These can vary
strongly with position. For this reason, it is best to keep the probe in a fixed position, and to
move the magnetic field relative to the probe by moving whatever is generating the magnetic
field.

Useful constants

permeability of free space μ0 = 4π x 10-7 Hm-1

number of turns in air solenoid coil 30
diameter of air solenoid coil 8.4 cm
number of turns in Helmholtz coil 320
diameter of Helmholtz coil 13.5 cm

Version 1.1, 01/10/07

 3

Section 1. the magnetic field due to current carrying conductors

According to Biot-Savart's law, the contribution to magnetic field dB at a point r due to a

∧
segment d l of current I is

μ0 1
dB = ⋅ I ⋅ 2 dlˆ × rˆ
4π r

Calculating the total magnetic field due to a flowing current (I) thus means evaluating an
integral over the path of the current. Analytic solutions can be given only for conductors with
certain symmetries.

The magnetic field of a circular conductor loop with radius R is:

μ0 2πR 2
B= ⋅I ⋅
4π (R 2 + x 2 )3 2
Here x is the distance on the axis, and B is in axial direction

Before taking any measurements with the axial B probe, you need to check for unwanted
effects due to background magnetic fields. First carry out the zero point adjustment of the
axial B-probe. This is done by inserting the magnetic B-probe into the magnetically shielded
space in the teslameter, and then pressing the zero-button, so that a reading of zero is
displayed. The background magnetic fields will appear as readings on the teslameter which
are present when no current is flowing. These effects can be reduced by using the
compensation adjustment of the teslameter. Again, press the zero button of the teslameter,
this time with the axial B-probe in its measuring position.

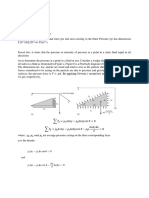
Figure: setup of the apparatus for a conductor loop.

Version 1.1, 01/10/07

 4

Set up the experiment as shown in the figure. Begin with the 40mm diameter conductor loop.
Position the axial B probe at the centre of the loop. Increase the current I from 0 to 16 A in
steps of 2A. Each time measure the magnetic field B. Plot graphs of B vs. I. Compare with
theoretical estimates.

At I=16A move the B-probe to the right and to the left step by step, measuring the magnetic
field B as a function of the space coordinate x up to distances of ±10cm in steps of 1cm. Plot
graphs of B vs. x. Compare with theoretical estimates.

Replace the 40mm conductor loop with the 80mm conductor loop and then with the 120mm
conductor loop. In both cases measure the magnetic field for a current of I=16A as a function
of the space coordinate x up to distances of ±10cm in steps of 1cm. Plot graphs of B vs. x.
Compare with theoretical estimates.

The magnetic field of an infinitely long wire is:

μ0 2
B= ⋅I⋅
4π r

Here r is the distance perpendicular to the wire and B is in the tangential direction.

Figure: setup of the apparatus for a straight conductor.

Now arrange the experimental setup as shown in the figure to measure the field around the
straight conductor. Remember that the field is tangential, but the B probe is only sensitive to
axial fields. It is necessary to position the axial B-probe perpendicular to and vertically
above the centre of the straight conductor. Changing the vertical distance corresponds to

Version 1.1, 01/10/07

 5

changing the tangential distance between the straight conductor and the axial B-probe.
Measure the magnetic field B for vertical distances up to ±3.0cm in steps of 0.5cm.

Plot a graph B vs. x. Compare with theoretical estimates.

Section 2. the axial magnetic field of an air solenoid.

The magnetic field inside an infinitely long solenoid with N turns in distance L is:

N
B = μ0 ⋅ I ⋅
L

Here B is in the axial direction, and does not change with distance.

The magnetic field on the axis of a solenoid of finite length L and radius R, the magnetic
field is:

N ⎛⎜ x+L 2 x−L 2 ⎞
B = μ0 ⋅ I ⋅ ⋅ − ⎟
(
⎜
2 L ( x + L 2 )2 + R 2
⎝ )
12
((x − L 2)
2
+R )
2 12 ⎟
⎠

Here x is the distance from the centre and B is in axial direction.

Figure: setup of the apparatus for a solenoid.

Set up the apparatus as shown in the figure. Use N=30 and L=15cm. Increase the current I
from 0 to 16 A in steps of 2A. Each time measure the magnetic field B at the centre. Plot
graphs of B vs. I. Compare with theoretical.

Now look at the effects of different coil lengths. Use lengths L of from 10 to 40 in steps of
5cm. In each case use current of I=16A. Plot graphs of B vs. L. Compare with theoretical.

Now use coil length of 15cm and current of I=16A. Measure the magnetic field for distances
along the axis of the coil up to ±20cm in steps of 2cm. Plot a graph of B vs. x. Compare with
theoretical estimates.

Version 1.1, 01/10/07

 6

Version 1.1, 01/10/07

 7

Section 3. the radial and tangential magnetic field of a coil

The magnetic field on the axis of a coil radius R with N turns can be approximated by

μ0 2πR 2
B= ⋅ NI ⋅
4π (R 2 + x 2 )3 2
where x is the distance from the centre and B is in the axial direction.

The magnetic field surrounding a coil can be expressed in spherical polar coordinates r, θ and
φ, where r is distance from centre of coil, θ is the azimuthal angle relative to the axis and φ is
the polar angle relative to the circumference. The magnetic field has components

μ0 2πR 2 cos(θ )
Br = ⋅ NI ⋅
4π r3

μ0 πR 2 sin(θ )
Bθ = ⋅ NI ⋅
4π r3

where Br is in the radial direction, and Bθ is in the azimuthal direction.

Set up one Helmholtz coil, using the same experimental setup as for the current loop in
Section 1. Set the current to I=1.5A. Position the B-probe on axis at a distance where still
possible to read 0.15mT for magnetic field. Now take measurements of magnetic field while
changing the orientation of the coil. Go in steps of 30° up to 360° (i.e. the same as the
positions of the hours on a clock).

To measure the tangential component of magnetic fields is tricky, because B-probe is axial.
The axial B-probe must be turned to one side of the optical track. Ask the demonstrator how
to set this up. Make sure the distance is the same as for the radial measurements. Now take
measurements while changing the orientation. Go in steps of 30° up to 360° (i.e. the same as
the positions of the hours on a clock).

Plot graphs of B vs. orientation. Compare with theoretical.

Use your values of the radial and tangential components of B to sketch a diagram showing
the direction (i.e. vectors) of the magnetic field in the circle around the coil.

Version 1.1, 01/10/07

 8

Section 4. the axial magnetic field of a pair of Helmholtz coils

Place a single Helmholtz coil on the optical track, and measure the axial magnetic field of at
distances up to ±10cm in steps of 1 cm (using the same method as for the current loops in
Section 1).

A pair of Helmholtz coils is used to create a homogeneous magnetic field. Now look at the
combined magnetic field of a pair of Helmholtz coils. Set-up the Helmholtz coil on the
optical track, with wiring as in the figure. Use the B-probe to measure the magnetic field in
the region between the two coils, i.e. from the centre of one coil to the centre of the other.
Experiment with different separations of the Helmholtz coils until you find the optimum
separation for obtaining a homogeneous field (that is a field which is constant as a function of
distance). Plot graphs of B vs. x for three different separations not less than 5cm and not
greater than 20cm, including the separation you found which gave the most uniform axial
magnetic field between the coils.

Z A

Figure: wiring sense for Helmholtz coils.

Questions

(1) What is the direction and strength of the Earth's magnetic field in the Physics Lab?

(2) If the pair of Helmholtz coils were wired in the opposite sense to that in the figure, what
would the magnetic field be like between the Helmholtz coils?

References

1. H.C. Ohanian, "Classical Electrodynamics", (Allyn and Bacon, 1988). [QC631]

Version 1.1, 01/10/07