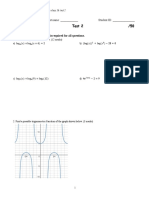
Unit #1 Test: Linear Systems Name: _Solubions Marking Summary: Knowledge/Understanding: questions #1 - 5 Application: questions #6-7 Thinking/Inquiry and Problem Solving: #8 - 9 Communication: all Total Marks: ‘MPM2D_ 50 1. Solve each linear system below by graphing. a) y=x-3 b) 2x+y=5 7~y tS 2y =10 ahyt lo 7 4 Y> hax Slay (4, +) [8 marks] “0-8 6-4-2MeMap Page 2 of 2. Solve the following linear system using substitution. [4 marks] @x-y-3 Se L. 6 EO) Qaxry=9 ay RA Dye (i-4y)> y=a-4(2.) Ved tx = Y 6x42 yr! ' NN 6x22 ea (21 } 3. Solve the following linear system using elimination. [4 marks] S _— ansayers > LORHIS yz 6S senayent T9 > Dowty = Yet Bales By = 483 YxtrTe B yo) x4 Ka | 4, Use either substitution or elimination to solve the following. [4 marks] ay ~ ~ 3a-2b+4=0 Os be YL+5>0 a -LENFY 20 ta-sb-1=0 > Ga-lyb-b =O YO ——MPM2D Page 3 of 5 5. Use either substitution or elimination to solve each of the following. [8 marks] a) 442y=-4e —> 4x My 2-4 = Yydy ek ety=9 > Dyetyr “ + betyso = ye A xy Unt dys ly & No salehvn . ofr6 b) 6x-y=-1 —9 Gye 3y-8x=2 “brah 6. Melissa takes her family to a burger stand. She orders 3 hot dogs and 2 hamburgers. The total cost is $15.95. The next week she returns to the same burger stand. This time she orders 4 hot dogs and 3 hamburgers and the total cost is $22.55. What is the cost of a hot dog? What Is the cost of a hamburger? [6 marks] Let bs cont of buyer CB) y ds cond of hot dey 6) BA trib 15.9 ES urd rb = 63-60. te E3b2 22ST nd tab +67 HA 2a y= TF —— . yd tliss re b=3.05 ud ~ Uf hob doy $2797 d~ 2.15 beer £3 65>Mpwed Page 4 of S$ 7. One type of granola has 30% nuts, by mass. A second type of granola has 15% nuts. What mass of each. type must be mixed to make 600g of granola that will have 2196 nuts? [6 marks] jo teak (on 5 ) Let x= 30% nh (er 4) ye Kt 260? —_ ry > b00 x= OOTY fat Sy 600C6-) > 3xt 17 no suk © moO .3 Céoe-y) #18 y S16 [yo O44 toldy 2126 7 / @p- ~0tS y= $7 2 LYvVy of 30% are od +360 iy oO hai x on Y MK G00-S6O Ch nde. 300s ok 45 es yo Kerri works for an automotive mechanice. She has two “jobs”: installing new tires and performing an oil change. Installing tires takes her 45 minutes. An oll change takes her 20 minutes. One particular week she logs 64 jobs taking a total of 30.5 hours. How many times did she install a new set of tires? Led tz membe of tire lash He buns Ct Nembr of o|( choayes O fye= 64 = Fa64-c 3u.5 hous Sptuntr . ; @ fs travc= [630 = Jyyo mk 8. [6 marks) yard noe oS hot dons x h cb €rb4-€ ibs @ booty Us (O4-c) #286 = WSO t= OX regan use Free = [830 a gy hie ches = 35e = 7180 fdr ol chenses ez 4MPM2D Page 5 of 5 9. Erik goes kayaking down a river. He starts by kayaking down the river (with the current) and travels 25 km in 2.5 hours. Erik then paddles up the river (against the current). After 3 hours he has only travelled 15 km up stream before getting tired. Assuming he paddled at the same water speed in both directions, how fast is the current? How fast could Erik travel with no current? (6 marks] Let be speed of reyak Ga shtl waked Eft, Cz Currant speod Chnd | O2sCkwte) = 2 @ 3 Ck tle 7% poo ts ke Ste sb O Hh@ DS C5 bet LF Ee ger (fre) e2 bs 642.7 Is po 7s ke77, Ge te ct hy 0% Currenh 9. SlendA , koa can ge Qo km(h wf ne coreah.