NEWTON RAPHSON METHOD

Introduction

The Newton-Rap son method, sometimes known as the Newton Method, is a useful tool
for numerically solving equations Similarly to much of differential calculus. It's based on the
straightforward concept of linear approximation. Newton's Method When utilized correctly, it
can generally zero in on a root with deadly efficiency. Section 2.1, where the fundamental
formula is obtained. Section 2.2, where the technique is geometrically understood; and, of
course, Section 6, where the problems reside, are the most important parts of these notes. The
genesis of the Newton Method is detailed in Section 3, which is rather peripheral but maybe
fascinating. One of the most extensively used methods for root discovery is the Newton-Rap-
Hson approach. Newton's approach may be easily expanded to the challenge of finding solutions
to a system of non-linear equations. Furthermore, as we approach the root, the strategy may be
proven to be quadratically convergent. Unlike the bisection and false position approaches, the
Newton-Rap-Hson (N-R) methodology only requires one initial number, x0, which we'll call the
root's initial estimate. We may rewrite the function f (x) using a Taylor series expansion in (x-x0)
to demonstrate how the N-R technique works:

f(x) = f(x0) + f'(x0) (x-x0) + 1/2 f''(x0) (x-x0)2 + ... = 0 

Assume that your first bet becomes really near the authentic root. Then (x-x0) is tiny, and
most effective; the primary few phrases inside the collection are essential for figuring out the
authentic root given x0. We attain the N-R new release method for accomplishing a higher
approximation of the authentic root via way of means of truncating the collection at the second
one-term (linear in x):

Thus, the N-R technique calculates x1 by

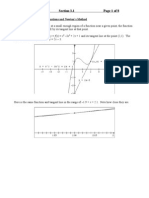
finding the tangent to the function f (x) at x=x0 and extrapolating it to cross the x-axis. When
possible, this point of intersection is used as the next approximation to the root, and the method
is continued until convergence is attained. Given the value of x = xi at the conclusion of the
iteration, we may calculate xi+1.

The Newton-Rap son technique is used to solve equations of the form f (x) = 0. We create
an initial guess for the root we're looking for, which we refer to as x0. The numbers x0, x1, x2,
x3. . The precise root should be created in the way outlined below. To do so analytically, we'll
need a formula for each approximation in terms of the preceding one; i.e., xn+1 in terms of an.
At the point (x0, f (x0)), the equation of the tangent line to the graph y = f (x) is the equation of
the tangent line to the graph y = f(x) at the point (x0, f(x0)) is y − f(x0) = f 0 (x0) (x − x0). The
formula above should be memorized. The Newton-Rap on approach, which we shall demonstrate
today, is used to solve f (x) = 0 equations. If the initial guess x0 is close enough, it will converge,
but defining what we mean by 'close enough' is problematic because it is highly situation-
specific. A diagram of the f (x) graph can help us choose an appropriate Initial estimate of x0 for
a given circumstance. The Newton-Rap son Method is another numerical method for estimating
the root of a polynomial. A Newton-Rap Hson Approach is an open approach to root discovery,
which means it only takes one starting estimate rather than two to arrive at a solution.