Exact SolutionsCouette Flow We will assume Parallel flow u#O,v=w=0 Consider 2 parallel plates as shown in the figure. The bottom plate is stationary And the top plate is moving with 1 = Ugg A PLP EEL AL. x Let us further assume that the flow is incompressible, viscous, steady, no body forces, laminar, fully developed. a ‘Also assume that the width of the plate is large in z direction such that au =0 xzFor a parallel ow u #0.v = w=0 Th 1 oy” \en continuity equation gives ou i oe =0 ax Ay faz Or u=uy,z) But Zo=0 So w= uy) only From momentum equations in erection 0 (ye ye we 9 a oa ou, ‘ot Oz Ox ‘Ox? dy? /0z* ech: a (at ae ao vercon—p (2 ua ys Bt) a Pay (Bg Ba A H z-direction 0 (Bryer +p) =- Lan ( Bee) From y and z momentum equations we can conclude that p # p(y, z) or p = p(X) only. From x momentum equation dp _— ( d*u ax “ae a But we have already established that p = p(x) and u = u(y) only. Then we can write oe =p (2) ‘y"Note that LHS is either a constant or function of y and RHS is either a function of x or constant. The equality is possible ‘only when both LHS = RHS = constant.So dp au — Nae = constant Now let us integrate this equation. Upon etn we get 1 dp u(y) = mE +Cy+G The boundary conditions are Aty=0,u=0 Aty=h, W = Ug, Solving for C,, C, and simplifying we obtain “inc (-#) is the non-dimensional pressure gradient When a@ = 0, zero pressure gradient When a > 0, favourable pressure gradient When a < 0, adverse pressure gradientThis is called simple or plane Couette flow In this case flow is purely due to friction from top plate Consider a # 0 = bebe(- ap ‘Then maximum happens when a@ > 0 |e. when zs 0 x qj ‘Similarly minimum happens when a < 0 |.e. when 2 >0 x‘Substituting backPlane Poiseuille Flow In this case both plates are fixed. ‘We will again assume parallel flow u # 0,v = w = 0. z Let us further assume that the flow is incompressible, viscous, steady, no body forces, laminar, fully developed. Also assume that the width of the plate is large in 2 direction such that 59 =0 ca Recall that for such a situation u = u(y) P=plx) a = Pu = constant ax" \ ae) =Upon integrating 1 dp u(y) = Grae? +CytG The boundary conditions are Aty=1v2, u=0 Aty=-hv2, u=0 Solving for C,, Cy and simplifying we obtain _ iW (_aP y w= (-Z) (: -5)Hagen Poiseuille Flow Consider flow through a circular pipe. Assume parallel flow. In cylindrical coordinates, this means u, # O,u, = ty = 0 ‘Also assume that the flow is steady, incompressible, viscous, laminar and fully developed and body forces are absent. As the flow is axis-symmetric, 4o= = Continuity equation gives ~ hats += Then u, # u,(z). Also as the flow is axis-symmetric, =0. Then u, # u.(@). Then u, = u,(r) only.t-momentum equation gives Oy’ QUE, Mo Me. Meh ®, »(2 (220) + +z ge om ut \ i Var 4 00° Xo 7r ar **\ ar Then p # p(r) @-momentum equation gives WE sR Pag «to 3 (Li) oR BR Be Then p # p(0) Then it follows that p = p(z) only. z-momentum equation gives MEE Pak (15 (-B) Sz) dp = ld =) = Constant (Arguing as before) dz \ rar ar) ) > = o , Fy 00 72Upon integration we get "Or Ud: dp ( lw. Upon integrating again w.rt. r get a l dp east tear + Boundary conditions Atr=R u,=0 Atr=0 =0 dr Solving for constants and simplifying we get R? ( dp r W=a (-2) (: a occurs atr=Oand uw. oh (_# =Oand tomas = a ae Where tsnay Q. Calculate the flow rate and the average velocity Uajyy relate itt MimaFlow rate is given by ® k 2 R Q= I ur)2ardr = I, t( 1 z) Qardr = 2Rtya, (= 0 2 Average flow velocity is given BY Uayy = 2 = omer z (-) al lz Skin friction coetficient 3 16 g=—— = 1" U2pectthing Rep Define hydraulic diameter 4A PetlcargD D== Where Rep is the Reynolds number based on diameter given by Rep =, For a cylindrical duct Poot cave? Note: for a duct with any generic cross-section Rey = —=—"* + D a1 _opep # 0 OARTurbulent Flow through a Pipe Laminar vs Turbulent Flow: ~ Laminar flow is nice and smooth = Turbulent flow involves irregular, stochastic motion-averaging is performed = Parallel flow can have 3D turbulence. Then mean flow will be parallel flow. = Turbulent flows have higher mixing, friction and heat transfer rates. Consider force balance in x direction LLLL Lees p*A — (p* — Ap*) A= 1,51 | ‘w Where S is the perimeter. Simplifying: A _ AptA oe ST Recall hydraulic diameter Here p* is the piezometric pressure And Uagrg = 2Rearranging Ap’ fol (5a ue, ) Where Q — (=p,.13 Using == yD NDT mea So if the friction factor is known, then knowing the geometry of the duct the pressure drop can be calculated if flow rate is known and vice versa. For a circular tube D,, = D ‘So we somehow need to know the friction factor. For a laminar flow we know from Hagen-Poiseuille flow that 64 PootlcargD = 4g = = fag Rep Rey 7 For pipe flow if Rep < 2000 => Laminar flow, if Re, > 2000 => turbulent flow For a turbulent Flow however f = f(Re, €) . Here € is the roughness parameter as is often described in terms of ¢/D which is called the relative roughness. This functional dependency is plotted in the Moody's Diagram Ap* Po Note: The above relation is sometimes given in terms of pressure head hy = (ly D Pg L Friction factor, f- Laminar flow iti [fe etRe ane Laminar low | {|| Transition fh Ta Complete turbulence, rough pipes ive roughness €/D = SS i L 23579 23579 23579 108 108 10” 108 Reynolds number, Re = VD/v trareduction to fluid mechanics and fluid machines, by 8.K. Som and G. Blows:= Outside the boundary layer, inertia forces >> viscous forces. = Within the boundary layer, viscous effects are large due to presence of velocity gradient. Viscous force are of the same order as inertia forces. (“¢ ) Inertia forces per unit volume are of the order . Viscous forces per unit volume are of the order 0 (#2) For these to be of comparable order of magnitude 2 Prootlie Yow foe |} =0([ w= (4) -o(3) Then 2 e “H I o(—)=o0 =0(— (i) =r) -°(ze) me o(#)=0(+) Then 6 increases with increase in L,p and with decreases with increase in Poor leo And 6/L decreases with increase in ReNon-dimensionalisation of the Navier Stokes equations Let us consider the 2D, Steady, incompressible Navier Stokes equations (note: this process can be extended to the unsteady, 3D, compressible Navier Stokes equations also). mass au SE gD el ax dy ‘Momentum - x («2+ 3t) = op, (Fu, eu OM a ay) ae TY ae ye? ‘Momentum - y um yet __ + ay ey PM ae ay) ay TAN ae Oe As the flow is incompressible, the energy equation gets decoupled. We will not non-dimensionalise it here. ‘Try it your self. To non-dimensionalise, we need suitable reference scales called non-dimensionalisation parameters. Let these be x y wee yey weL ‘Then writing the Navier Stokes equations in terms of these non-dimensional variables we getPia (PY) Hil ( Fur , Put L Na LB at ays aw * " AP yet Ot +(%-%) ax? aye?So the non dimensional, steady, 2D, incompressible N-S equations are given as au® av® +e ax* ay* aut | du* _——ap* (= + ==) Ox* Oe ae Re ax*? ay#? 1 (Fm eve (| SS Re \ ax® © ay*The boundary layer equations ‘The idea is to perform order of magnitude analysis within the boundary layer to evaluate if any terms can be dropped from the full N-S equations to make our life easier. L . Now, within the boundary layer, any distance xis of order —_| Similarly, x velocity u is of order x= OW) u= Olu) Then x* =~ =0(1) Then ut = = O(1) L Yoo ‘Similarly, any distance y within the boundary layer is of order | And pressure p is of order y= 066) p=O(pu2) tren yt =2 = 02) = 064) then pt =P = LOL p= = 001) PussConservation of mass gives Be Oo ox* — ay* So the order of magnitude equation becomes od) | b*) OU) 0") So for both terms to be of same order, v* = O(6*) First assumption for boundary layer theory, assume that the boundary layer is thin, i.e. 6< ) Re Oe*) Only way to get a non-trivial equation is by assuming — = ()(6**) . This is the second assumption for boundary layer theory. Re Then the order of magnitude equation becomes O(1) + OU) = 01 +005 Oe So the x- momentum equation simplifies to aut au* apt 1 (due abu ede __ oot 1 f Fue woe Tae ae Te (5)The y- momentum equation gives wr ove ae aye ae ar Re \ Get The corresponding order of magnitude equation will be —+ oy ou) OG") | Oe") 0112 5 9160 2. _ vaslee owe ol) Upon simplifying aN) ou) 5* = O(5*) + O(6*) oe * x (0% i) + ao) Multiplying throughout by O(5*) 2 2) ! 2, O(6**) + O(6**) = 01) +3 (016%) + 011)) What should be choice for order of Re 7 1 2 ‘You have to choose the same order as that for the x-momentum equation. So Ear te Then _ eg =~ 01+ (96406) y-momentum equation rig gives 0At any given x- station, as wr =o so p* = p*(x*) only. So op* _ dP —= Finally the boundary equations become: oy* oe ae deve Non-dimensional form Dimensional form “ ae mM 0 du av ax* — ay* ox dy aut au* dp * w+ re eel a nly ot) = fa, 56 ax* ay= dx* Re \ ay#? dx ay dx ~ dy? Unknowns are u and v. So 2 equations and 2 unknowns can easily be solved. Note: pressure p(x) is obtained from Solution of the outer flow inviscid equations.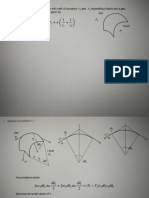Deane sess ge tance byw na wal nent ob ated vars, hae sane mas fo tg ms oro cae pn (68) x1 =o) ud ydy x Net tat 6 ‘Sirona can dine a mmantun cknas based on momentum defectInternal Flows: Developing and fully developed flow, concept of entrance length Developing Flow Fully Developed FlowBoundary layer separation Boundary yer ©“ eytinder pe ey we —h @ “p10 [Suicidal a WA eect hl weal ip OL nat heii: