MATHEMATICS-I LAB

MANUAL

I Sem EC /CS
(22MATS11)

BANGALORE COLLEGE OF ENGINEERING & TECHNOLOGY

BANGALORE-99

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

SCILAB
PROCEDURE:
1.Switch on your PC.
2.Go to all programs and open scilab 6.0.2.
3.Go to scinotes.
4.Write the coding/programs.
5.Save the file and use extension name .sci.
6.Then execute and go to the scilab console window for output.

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

EX:NO:1 2D PLOTS OF CARTESIAN AND POLAR CURVES
AIM:
To plot 2D plots of cartesian and polar curves by scilab.
TOOL:
Scilab
THEORY:
2D Polar plot
Polarplot creates a polar coordinates plot of the angle versus the radius rho.
theta is the angle from the x axis to the radius vector specified in radians; rho is
the length of the radius vector specified in data space units. A polar coordinate
system is determined by a fixed point, a origin or pole and zero direction or
axis.
2D cartesian plot
A cartesian curve is a curve specified in cartesian coordinates.
In the cartesian system the coordinates are perpendicular to one another with the
same unit length on both axes.

SOURCE CODE:
2D Polar plot:
a) t=0:0.01:2*%pi;
clf();polarplot(sin(7*t),cos(8*t))
clf();polarplot([sin(7*t')sin(6*t')],[cos(8*t'),cos(8*t')],[1,2])

b) theta=0:0.01:2*%pi;
a=1
r=a*(1-cos(theta));
polarplot(theta,r)

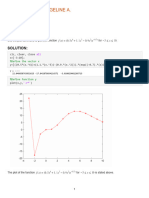
2D cartesian plot:
x=-2:0.01:2;
y1=sqrt(1-x^2);
y2=-sqrt(1-x^2);
plot(x,y1,x,y2)

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

OUTPUT:

2D Polar plot:

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

2D cartesian plot:

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

RESULT:
Thus the 2D plots of cartesian and polar plot are successfully executed.

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

EX:NO:2 FINDING ANGLE BETWEEN POLAR CURVES,
CURVATURE AND RADIUS OF CURVATURE OF A GIVEN CURVE
AIM:
To find angle between polar curves, curvature and radius of curvature of a given
curve.
TOOL:
Scilab
THEORY:
In the polar coordinates system, ordered pair will be (r,0). The ordered pair
specifies a points location based on the value of r and the angle 0.
The radius of curvature is the reciprocal of the curvature for a curve, it equals
the radius of the circular arc which best approximates the curve at that point.
The radius changes as the curve moves. the curvature vector length is the radius
of curvature.
SOURCE CODE:
(i) t=-%pi:%pi/32:%pi;
a=1;
r=1-cos(t);
polarplot(t,r)
t1=-%pi:%pi/32:%pi;
r=cos(t1);
polarplot(t1,r);

(ii) r=input('enter the radius of the circle=')

theta=linspace (0,2*%pi,100);
x=r*cos(theta);
y=r*sin(theta);
circle=[x,y];
plot(x,y);
xlabel('x');
ylabel('y');
title('circle of given radius',"fontsize",4);

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

OUTPUT:
(i)

(ii)Enter the radius of circle:5

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

RESULT:
Thus the angle of curvature and radius of a given circle was executed
successfully.

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

EX:NO:3 FINDING PARTIAL DERIVATIVES AND JACOBIANS
AIM:
To find the partial derivatives and jacobians in scilab.
TOOL:
Scilab
THEORY:
A jacobian matrix is a special kind of matrix that consists of first order partial
derivatives for some vector function. Jacobian is the determinant of the jacobian
matrix. The matrix will contain all partial derivatives of a vector function. The
main use of jacobian is found in the transformation of coordinates.
SOURCE CODE:
function ydot=f(t, y)
ydot=A*y
endfunction
function J=Jacobian(t, y)
J=A
endfunction
A=[10,0;0,-1]
y0=[0;1];
t0=0;
t=1;
y=ode("stiff",y0,t0,t,f,Jacobian)
disp("solution given by the solver")
disp(y)
disp("exact solution")
disp("y=")
disp(expm(A*t)*y0)

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

OUTPUT:

"solution given by the solver"

0
0.3678794
"exact solution"
"y="
0
0.3678794

RESULT:
Thus the partial derivatives and jacobians program was executed successfully.

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

EX:NO:4 SOLUTIONS OF FIRST ORDER ORDINARY
DIFFERENTIAL EQAUTION AND PLOTTING THE SOLUTION
AIM:
To determine the solutions of first order ordinary differential equation and plot
the solution curves.
TOOL:
Scilab
THEORY:
The first order means that the first derivative of y appears but no higher order
derivatives do. It represents the rate of change of one variable with respect to
another variable. A first order differential equation is defined by an equation :
dy/dx=f(x,y) of two variables x and y with its function f(x,y) defined on a
region in the xy-plane. the differential equation in first order can be written as
y’=f(x,y) or
(d/dx)y=f(x,y)
SOURCE CODE:
(i)

function dx=f(x, y)
dx=-2*x-y;
endfunction
y0=-1;
x0=0;
t=0.4;
sol=ode(y0,x0,t,f);
disp(sol,"answer");
plot2d(x,sol,5)
xlabel('x');
ylabel('y(x)');
xtitle('y(x)vs x');

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

(ii)

funcprot(0)
clf;
function dx=f(x, y)
dx=exp(-x);
endfunction
y0=0;
x0=0;
x=[0:0.5:10]
sol=ode(y0,x0,x,f);
plot2d(x,sol,5)
xlabel('x');
ylabel('y(x)');
xtitle('y(x)vs x');

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

OUTPUT:

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

RESULT:
Thus the solution of first order differential equation and plotting the solution
curves was executed successfully.

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

EX:NO:5 FINDING GCD USING EUCLID’S ALGORITHM
AIM:
To find the GCD numbers of two variables using euclids algorithm.
TOOL:
Scilab
THEORY:
The Euclidean algorithm or Euclid algorithm is an efficient method for two
integers, the largest number that divides them both without a reminder.it can be
used to reduce fractions to their simplest form and is a part of many other
number theoretic and cryptographic calculations.
The Euclidean algorithm for finding GCD(A,B)is as follows:
If A=0 then GCD(A,B)=B, Since the GCD(0,B)=B and we can stop.
If B=0 then GCD(A,B)=A, since the GCD(A,0)=A and we can stop.

SOURCE CODE:
clc;
clear;
function gcd(a, b)
x=a
y=b
while y~=0
r=modulo(x,y)
x=y
y=r
end
mprintf("gcd(%d,%d)=%d",a,b,x)
endfunction
n1=input("enter first no:")
n2=input("enter second number:")
gcd(n1,n2)

RESULT:
Thus the GCD of two numbers using euclids algorithm was executed
successfully.

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

OUTPUT:

Enter first number:10

Enter second number:20
Gcd(10,20)=10

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

EX:NO:6 SOLVING LINEAR CONGRUENCES ax=b(mod m)
AIM:
To solve linear congruences by scilab.
TOOL:
Scilab
THEORY:
A congruence of the form ax=(mod m) where x is an unknown integer is called
a linear congruence in one variable. A linear congruence is a congruence
relation of the form ax=(mod m) where a,b,m Z and m>0.
Numbers are congruent if they have a property that the difference between them
is integrally divisible by a number(an integer).The number is called the modulus
and the statement is treated as congruent to the modulo.
SOURCE CODE:
a=8;
b=12;
m=28;
v=int32([a,m]);
d=gcd(v);
a1=a/d;
b1=b/d;
m1=m/d;
function yd=f(x)
yd=(a1*x)-b1
endfunction
disp('k is the unique solution of the equation')
for i=0:m1
x=i;
p=f(x);
if (modulo(p,m1)==0)
k=x;
break;
end
end
s1=k;
s2=k+m1;
s3=k+(m1*2);
s4=k+(m1*3);

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

disp('solutions of the original equation at d=4')
disp(s1)
disp(s2)
disp(s3)
disp(s4)

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

OUTPUT:

'k is the unique solution of the equation'

'solutions of the original equation at d=4'
5
12
19
26

RESULT:
Thus the linear congruences was solved and executed successfully.

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

EX:NO:7 SOLUTION OF SYSTEM OF LINEAR EQUATIONS USING
GAUSS SEIDAL ITERATION
AIM:
To find the solution of system of linear equations using gauss seidal iteration
method .
TOOLS:
Scilab
THEORY:
In numerical linear algebra, the gauss-seidal method is an iterative method used
to solve a system of linear equations. Gauss seidal method is an improved form
of jacobi method also known as the successive displacement method. For a
system of equations Ax=B, we begin with an initial approximation of solution
vector x=x0,by which we get a sequence of solution vector x1,x2,…xk.
SOURCE CODE:
clc;
clear;
a=[12,3,-5;1,5,3;3,7,13];
b=[1,28,76];
x=[0,0,0];
n=input("enter no of iterations;")
for i=1:n
x(1)=(b(1)-a(1,2)*x(2)-a(1,3)*x(3))/a(1,1);
x(2)=(b(2)-a(2,1)*x(1)-a(2,3)*x(3))/a(2,2);
x(3)=(b(3)-a(3,1)*x(1)-a(3,2)*x(2))/a(3,3);
disp("x1,x2 and x3 after"+string(i)+"iterations");
disp(x);
end

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

OUTPUT:

enter no of iterations 3

"x1,x2,x3 after1iteration"

0.0833333 5.5833333 2.8205128

"x1,x2,x3 after2iteration"

-0.1372863 3.9351496 3.7589086

"x1,x2,x3 after3iteration"

0.6657579 3.2115033 3.9632464

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

RESULT:
Thus the solution of system of linear equations using gauss seidal iterations was
computed successfully.

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

EX:NO:8 NUMERICAL SOLUTION OF SYSTEM OF LINEAR
EQUATIONS,TEST FOR CONSISTENCY AND GRAPHICAL
REPRESENTATION
AIM:
To solve the system of linear equations ,test for consistency and graphical
representation .
TOOLS:
Scilab
THEORY:
The solution set of the system of linear equations is the set of the possible
values to the variables that satisfies the given linear equation.
A system of linear equations is a collection of one or more linear equations
involving the same variables. Graphing can be used if the system is inconsistent
or dependent. If the two lines are parallel, the system has no solution and is
inconsistent. If the two lines are identical, the system has infinite solutions and
is a dependent system.
SOURCE CODE:
(i) SOLUTION OF SYSTEM OF LINEAR EQUATIONS

clc
n=input("enter no of variables")
disp('enter the coefficient matrix,rowwise')
for i=1:n;
for j=1:n;
A(i,j)=input("")
end
end
disp("enter the constant matrix,column")
for i=1:n;
c(i)=input("")
end

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

disp(A)
disp(c)
D=inv(A)*c
disp(D)

(ii) TEST CONSISTENCY

clc
N=input("enter no of variables")
disp('enter the coefficient matrix,rowwise')
for i=1:N;
for j=1:N;
A(i,j)=input("")
end
end
disp("enter the constant matrix,column")
for i=1:N;
C(i)=input("")
end
disp(A)
disp(C)
if rank(A)==rank([A c])then
if rank(A)==min(size(A))then
mprintf("\n system of equation has unique solution:\n")
else
mprintf("\n system of equation has infinitely many solution:\n")
end
if rank(A)<>rank([A C]) then
mprintf("\n system of equation has no solution:\n");
D=inv(A)*C

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

 disp(D)
end
end

(iii) SYSTEM OF LINEAR EQUATION BY GRAPHICL REPRESENTATION

clear
clc
xset('window',1)
xtitle("my graph","x axis","y axis")
x=linspace(1,3,30)
y1=3-x
y2=%e^(x-1)
plot(x,y1,"o-")
plot(x,y2,"+-")
legend("3-x","%e^(x-1)")
disp("from the graph, it is clear that the point of intersection is nearly x=1.43")

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

OUTPUT:
(i) SOLUTION OF SYSTEM OF LINEAR EQUATIONS

Equation : 2x+y+z=5
x+y+z=1
x-y+2z=1
enter no of variables 3
"enter the coefficient matrix,rowwise"
2
1
1
1
1
1
1
-1
2
"enter the constant matrix,column"
5
4
1

2 1 1
1 1 1
1 -1 2

5
4
1

1
2.0000000
1.0000000

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

(ii) TEST CONSISTENCY

enter no of variables 3
enter the coefficient matrix,rowwise''
4
6
5
9
2
4
9
6
2
enter the constant matrix,column
1
7
9
4. 6. 5.
9. 2. 4.
9. 6. 2.
1
7
9
system of equation has unique solution:
1.1153846
0.0961538
-0.8076923

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

OUTPUT:
(iii) SYSTEM OF LINEAR EQUATION BY GRAPHICL REPRESENTATION

RESULT:
Thus the numerical solution of system of linear equations, test for consistency
and graphical representation was executed successfully.

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

EX:NO:9 COMPUTE EIGEN VALUES AND EIGEN VECTORS AND
FIND THE LARGEST AND SMALLEST EIGENVALUE BY
RAYLEIGH POWER METHOD
AIM:
To compute the eigen values and eigen vectors and find the largest and smallest
eigen value by Rayleigh power method.
TOOLS:
Scilab
THEORY:
Rayleigh quotient iteration is an iterative method, that is, it delivers a sequence
of approximate solutions that converges to a true solution in the limit. Power
method normalizes the products Aq(k-1) to avoid overflow/underflow, therefore
it converges to x1(assuming it has unit norm).The power method converges if
is dominant and if q(0) has a component in the direction of the corresponding
eigenvector x1.It is used in the min-max theorem to get exact values of all
eigenvalues.
SOURCE CODE:
(i) Compute eigen values and eigen vectors
clc;
clear;
A= input('Enter the matrix:');
disp(A)
x=input('Enter the initial approximation to the eigenvector:');
disp(A)
[nA,mA]=size(A)
[nx,mx]=size(x)
if (nA<>mA) then
mprint("matrix must be square\n")
abort
else if (mA<>nx) then
mprint("matrix compatible dimension between A and b")
abort
end
n=nA
e=zeros(1,1)
while(1)do
for i =1:n
z(i)=0

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

 for j=1:n
z(i)=z(i)+A(i,j)*x(j)
end
end
zmax=abs(z(1))
for i=2:n
if abs (z(i))> zmax then
zmax = abs(z(i))
end
end

(ii) Largest eigen value and eigen vector

clear;clc;close();
A=[3 0 1;2 2 2;4 2 5];
disp(A,'the given matrix is')
u0=[1 1 1]';
disp(u0,'the intial vector is')
v=A*u0;
a=max(u0);
disp(a,'first approximation to eigen value is');
while abs(max(v)-a)>0.002
disp(v,"current eigen vector is")
a=max(v);
disp(a,"current eigen value is")
u0=v/max(v);
v=A*u0;
end
format('v',4);
disp(max(v),'the largest eigen value is:')
format('v',5)
disp(u0,'the corresponding eigen vector is:')

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

OUTPUT:
(i) Enter the matrix: [2,-1,0;-1,2,-1;0,-1,2]
2. -1. 0.
-1. 2. -1.
0. -1. 2.
Enter the initial approximation to the eigenvector: [1;0;0]
2. -1. 0.
-1. 2. -1.
0. -1. 2.
The required eigenvalue is :3.414214
the required eigenvalue is
0.708459 -1.000000 0.705754

(ii)
the given matrix is
3. 0. 1.
2. 2. 2.
4. 2. 5.
the intial vector is
1.
1.
1.
first approximation to eigen value is
1.
current eigen vector is
4.
6.

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

 11.
current eigen value is
11.
current eigen vector is
2.0909091
3.8181818
7.5454545
current eigen value is
7.5454545
current eigen vector is
1.8313253
3.5662651
7.1204819
current eigen value is
7.1204819
current eigen vector is
1.7715736
3.5160745
7.0304569
current eigen value is
7.0304569
current eigen vector is
1.7559567
3.5042118
7.0081829
current eigen value is
7.0081829
current eigen vector is
1.7516742

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

 3.5011505
7.0022666
current eigen value is
7.0022666
the largest eigen value is:
7.
the corresponding eigen vector is:
0.25
0.5
1.

RESULT:
Thus the eigen value and eigen vectors can be computed by Rayleigh power
method. Also the largest and smallest eigen values also computed and executed
successfully.

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

EX:NO:10 APPLICATIONS OF MAXIMA AND MINIMA OF TWO
VARIABLES
AIM:
To find the maxima and minima of two variables.
TOOLS:
Scilab
THEORY:
Maxima and minima are the peaks and valleys in the curve of a function.In
calcules,we can find the maximum and minimum value of any function without
even looking at the graph of a function.maxima will be the highest point on the
curve within the given range and minima would be the lowest point on the
curve.
SOURCE CODE:
clc();clear;
function y=f(x)
y=x+(1/x);
endfunction
//calculation
//dy/dx=1-(1/x^2)=0 for maxima or mimima
//x=1 or -1
//at x=0 y=infinte is maxima value
//minima value of y at x=1
ymin=f(1)
disp(ymin,'maxima value of given function is infinite and minima value is')

OUTPUT:
maxima value of given function is infinite and minima value is 2
RESULT:
Thus the maxima and minima values are computed successfully by scilab.

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE

PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE
PREPARED BY:ANUSUYA.P ,ASSISTANT PROFESSOR/ECE,BCET-BANGALORE