Infinite Impulse Response Filters 5.103 pein and Answers 4. Give the magnitude function of Butterworth filter. What is the effect of L wring order of N on magnitude and phase response? ‘The magnitude function of the Butterworth filter is given by ; it |#(Q)| = ————___ N = 1, 2,3,... [i+ (@)") where NV is the order of the filter and Q, is the cutoff frequency. The magnitude response of the Butterworth filter closely approximates the ideal response as the order N increases. The phase response becomes more non-linear as N increases, 1. Give any two properties of Butterworth lowpass filters | (AU ECE Nov’06) 1. The magnitude response of the Butterworth filter decreases monotoni- cally as the frequency (2 increases from 0 to oo. 2 The magnitude response of the Butterworth filter closely approximates the ideal Tesponse as the order NV increases. 3. The poles of the Butterworth filter lie on a circle. 4 Mat are the properties of Chebyshev filter? (AU ECE Nov’'06) 1, 2a 7 The magnitude Tesponse of the Chebyshev filter exhibits ripple either in Passband or in Stopband according to type. h The Poles of the Chebyshev filter lie‘on an ellipse. Give ; Liter, he ©quation for the order of N and cut off frequency Q. of Butterworth Onder of the filter log = ‘ = er as ng Stopband attenuation at stopband frequency ©, attenuation at passband frequency 2. 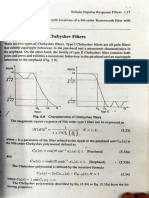: 2 See (10a, _ 1)aW,5.104 Digital Signal Processing 5. Give the Chebyshev filter transfer function and its magnitude respoy mise ‘The transfer function of Chebyshev filter is given by 1 A la 14 jeCw #)| where € is a parameter of the filter related to the ripple in the Cy(z) is the N’ th order Chebyshev polynomial defined as ep Cn(e) = cos (N cos? z)for |x|<1 Cy(2) =cosh(Ncosh-z) for |x| >1 ‘The magnitude response is shown in Fig. 1. 6. Poles of ee rth, i ea ilter ie on an ellipse True/False- : 7. Poles of Ch True. i le on an ellipse True/False 8. Chebyshev filter k True/False Pols re cls oan tan then Bute True. ; 9. A causal and stable IIR filter cannot The. have linear phase TraeInfinite Impulse Response Filters 5.105 ‘ Distinguish between the frequency response Of Chebyshev type 1 filter for N 1 odd and N even. ‘The frequency response curye starts from uni X 4 lin ity for odd Values of N, and starts from 7a for even values of N. 11, Distinguish between the frequency response of Chebyshev type I and type It fiers. Fig. 2° “Tre Chebyshev filters are all-pole filters that exhibit equiripple behaviour in te passband and @ monotonic characteristics in the stopband. On the other- $4 the family of type I Citys at els a Sa ‘eee monotonic behaviour in the passband and an equiripple behaviour in Sopband, ‘ Oe ch inn a Butterworth filter transfer junction and ts magnitude characteristics Te “rent orders of the filter. "2Usfer function of a Butterworth filter is given by “HGQ) = — 8 % 1t+j (2) me characteristics for different order ofthe filter are-shown in order N, major minor and axis of an lips incase ! te5.106 Digital Signal Processing The order N of Chebyshev filter is given by where a, is stopband attenuation at stopband frequency 2, and Oy is attenuation at passband frequency 9. The major and minor AX€5 Of the elinns are given by Y/N 4 y-1/N AN _ 1)" sa, a | tenn, [tae where p = e~! 4 /T 4 e-2 and e = 190195 —] 14, What are the parameters that can be obtained from the Chebysher fle specification? (AU ECE May't7) From the given Chebyshey filter specifications we can obtain the parncen Uke the order of the filter 1, e, transition ratio k, and the pols of the fi as Trot ePresion forthe location of poles and zeros of a Chebyshev tt 1, The zeros of the Chebyshev type If filter are : =; ee Taos ka1.N. "De Poe ofthe Chebyshev ype Str are ~ T+ ite k=1,....N 2,04 ee Se q kaha, f poles of a Chebyshev type 1 file” Alter can be found by using the forml4 += aco06 + jbsin gy k=1,2,...N ~Infinite Impulse Response Filters 5.107 here Nis the order of the filter w ; mee d= 5+ ( aH) k= 1,2... . tn pon a=2, | ———_ =, # pln 4 way : passband frequency et+Vi+e? e=viel —1 Op = = passband attenuation \ 11. Give the expression for location of, poles of. normalized Butterworth. filter. ‘ (AU ECE May’ 07). (AU EEE’ '07) ‘Tne poles of the Butterworth filter is given by sp =elte k=1,...N eit no Bias jn 0h aor Nis order of the filter. It Distinguish between Butterworth and Chebyshev (Type-1) filter 1. The magnitude response of Butterworth filter decreases monotonically as the frequency 9 increases from 0 to 00, whereas the magnitude response of the Chebyshev filter exhibits ripple i in the passband and monotonically ing in the stopband. E a band is more in Butterworth filter compared | to Chebyshev + The Poles of the Butterworth filter lie on a circle whereas the poles of the byshev filter lie on an ellipse. * For the same specifications the number of poles in Butterworth filter are ae when compared to Chebyshev filter, i.e:, the order of the Chebyshev ter is less than that of Butterworth. * Be °W One can design digital filters from analog filters? ; a) we desired digital filter specifications into those for an equivalent ana- wy : ve the analog transfer function for the analog OES5.108 Digital Signal Processing (©) Transform the transfer function of the analog prototype into an equivalent digital filter transfer function. 20. Mention any two procedures for digitizing the transfer function of an analog JSilter The two important procedures for digitizing the transfer function of an analog filter are (a) Impulse invariance method (b) Bilinear transformation method 21. What are the properties that are maintained same in the transfer of analog filter into a digital filter? (a) The j-axis in the s-plane should map into the unit circle in the z-plane. Thus there will be a direct relationship between the two frequency vari ables in the two domains. (b) The left half plane of the s-plane should map into the inside of the circle in the z-plane. Thus a stable analog filter will be converted stable digital filter. 22. Physically realizable and stable HR. filters cannot have linear phase. Pr Linear phase filter must have a system function that satisfies the condition H(z) = t2-" (271) where 2. represents a delay of N units of time. But if this is the every pole inside the unit circle there must be a pole outside the unit ci Hence the filter would be unstable, Consequently a causal and stable cannot have linear phase. 23, What do you understand by backward difference? One of the simplest method for conve e m erting an analog filter into a digital to approximate the differential equation by an equivalent differential eee = V(nT) ~ y(n - ien¥O| = wet) — wn? = 7) _ u(r) ~v(n-1) of The above equation is known as backward difference’ equation. 24. What is the mapping procedure between scplane and plane i ‘ of mapping of differentials? What is it's characteristics? ‘=infinite Impulse Response Filters 5.109 mapping procedure between s-plane and z-plane in the method of mapping I differentials is given by H(z) = H(s) ik oh ‘The above mapping has the following characteristics (a) The left half of s-plane maps inside a circle of radius 1/2 centered at z = 1/2 in the zeplane. (0) The right half of s-plane maps in to the region outside the circle of radius 1/2 in the z-plane. () The j-axis maps on to the perimeter of the circle of radius, 1/2 in the zplane. * 8 Whatis the matched z-transformation? : tis a method of converting an analog filter into an equivalent digital filter. eo the system function of the analog filter is expressed in the factored M , II (s - zx) H(s) = =+$—__ TI (s — Pe) , k=1 A : i. {+,} are the zeros and {p,} are the poles of the filter. Then the system on of the digital filter is fha-e#t=) H(z) =" N TIL G@ —eT2-4) ‘ eT Ti -~ 'S the sampling interval. is lng," by impulse invariant method of designing IIR filter? “tia oe of digitizing an analog filter, the impulse response of resulting 18 a sampled version of the impulse response of the analog filter, te, “* ®Xbress the transfer function of analog filter in partial fraction form, * uit Ck Hale as5.110 Digital Signal Processing Then the transfer function of digital filter can be obtained using the transfor- mation 1 T= etal $-Pk : H “ Ck ie, H(2)= vie T— emt z-1 k=l 27. By impulse invariance method obtain the digital filter transfer function and the differential equation of analog filter H(s) = Sai nae ~ s+ A(t) h@)= ee ee A= ets = n=0 For H(s) The differential equation can be obtained from Yo X(s) s+1 s¥() +¥ (8) = X(s), Taking inverse Laplace transform on both sides we get Sy(t) + ul) = a(t) 28. Obtain the impulse response of digital filter corresponding to: with impulse response h(t) =, 0.5e~™* and with a sampling using impulse invariance method. Given ha(t) = 0.5e~2 ha(nT) = 0.56727 . oO H(z) =0.5 (e771) ned ne [reer T =1 sec '. Hp) =e 1-e7*z-1 © 1 =0.1352-7Infinite Impulse Response Filters 5.111 impulse invariant method is not preferred in the des: lowpass filter? — invariance method, the mapping from s-plane to 2, nate is many pone, 1» all the poles in the s-plane between the intervals (2-1) a T ign of IIR filter other pede (for k = 0,1,2...) map into the entire z- plane, Thus, there is an infinite Tuber of poles that map to the same location in the z-plane, producing alasing effect. Due to spectrum aliasing the impulse invariance method is jate for designing highpass filters. That is why the impulse invariance ethod is not preferred in the design of IIR filter other than lowpass filters. ‘Give the bilinear transform equation between s-plane and z-plane 2 fics! Pat tere 1 Physically realizable and stable IIR, filters cannot have linear phase. True/False. The. . 2 Obain the digital filter transfer function if all poles of analog filter are spec- fied. ‘ ; Fall poles of = filter are specified the system function can be written the analog filter and {cx} are N ai) = > where {px} are poles of “aol Ea Now the above system function can be transformed io digital ag Nw To = sampling interval H(z) = rer Sie where T' = 5! 4 a ing linear transformation is a mapping | So tbe unit circle in the 2+ -plane only once, th ‘ponents, “enaping from the s-plane to the 2-plane in 2 1-5 a2 aad [; +2 4 the properties of the bilinear transformation? forms the left half of s-plane at evoding aliasing of HeQUENY bilinear transformation i that one mapping ne-t0-0! ce tion is and vi "Te Mapping for the bilinear transforma corres sod g point 8 is we point z, there is exactly 0m R5.112 Digital Signal Processing 35. 36. Write a short note on prewarping. 37. 38. 2. The j®-axis maps on to'the unit circle |z| = 1, the left half of the s-plane maps to the interior of the unit circle |z| = 1 and the right half of the s-plane maps on to the exterior of the unit circle |z| = 1. What is warping effect? What is its effect on magnitude and phase response? The relation between the analog and digital frequencies in bilinear transforma- tion is given by eT im tan i Dapaged For smaller.values of w there exist linear relationship between w and 92. But for large values of w the relationship is non-linear. This non-linearity introduces distortion in the frequency axis: This is known as warping effect. This effect. compresses the magnitude and phase response at high frequences. The effect of the non-linear compression at high frequencies can bé pensated. When the desired magnitude response is piece-wise co frequency, this compression can be compensated by introducit prescaling, or prewarping the critical frequencies by using the fo: wy ' A= Fan a What are the advantages and disadvantages of bilinear Advantages : 4. The bilinear transformation provides one-to-one mapping. 2. Stable continuous systems can be mapped into realizable, systems. 3. There is no aliasing, Disadvantages 1. The mapping is highly non-linear producing frequency col ; high frequencies, “— 2 Neither the impulse response nor the phase response of the 4 is preserved in a digital filter obtained by bilinear transforn Distinguish between recursive realization and non-recursive rea For recursive realization the present output y(n) is a function o} past and present inputs. This form corresponds to an Infinite-Im (mR) digital filter.Infinite Impulse Response Filters 5.113 n-recursive realizations the current output y(n) is a function of only past ices inputs. This form corresponds to an Finite Impulse Response (FIR) digital filter. y, What are the different types of structures for realization of IIR systei,: The different types of structures for realization of IIR system are ()Direct-form I structure, form II structure, (iv) Cas Lattice-ladder structure. ii) Direct-form I structure (iii) Transposed direct- ‘cade form structure, (v) Parallel form structure (vi) 4 Draw the direct-form I realization Structure of a 3rd order system (MU Oct’ 95, Oct’ 98) x0) bo y(n) . ; Draw tne Seneral realization structure in direct-form I of IIR system, (MU Apr’ 96) x(n) by yin) :5.114 Digital Signal Processing 42. Give direct-form I and direct-form II structure of second drder rystel real. ization. (MU Oct’ 99, Apr’ 2000, Oct” 2000, Oct’ 96) Direct-form I realization of a second order system . 43. How many number of additions, multiplications and memory loc required to realize a system H(z) having M zeros and N poles i: form I realization (b) direct-form IT realization? (a) The direct-form I realization requires M + N+1 tions and M+ N+1 memory locations. (b) The direct-form II realization requires M + N41 ditions and the maximum of (M, N) memory locations. 44. What is the main advantage of direct-form I realization direct-form I realization? In direct-form II realization, the number of memory locations than that of direct-form I realization. : 2Infinite Impulse Response Filters 5.115 the cascade structure direct-form [1 realization of 6th order filter, W rem Define signal flow graph. Asignal flow graph is a graphical representation of the relationship between the variables of a set of linear difference equations, - »- 41, Draw the signal flow graph of first order digital filter. x(n) bo y(n) 4 What is transposition theorem and transposed structure? atl (Oct’ 95) The transpose of a structure is defined by the following Sa "4 Reverse the directions of all branches in the signal flowgraph. iterchange the ii input and outputs. ti Reverse the roles of all nodes in the flow graph. () Su umming points become branching points. “) Branching Points become summing points. ions of all branch ing to transposition theorem if we seveate ee saa a fu Smittance and interchange the input and output pe system ion Temains unchanged. = nd order system. the transposed direct-form II structure of IIR seco} y(n), x(n) by5.116 Digital Signal Processing 50. Draw the parallel form structure of IR filter. « A parallel form realization of an IIR syste! partial fraction expansion of H(z). N H(2)=C+)> k=l = C+ H(z) + Hale) +---Hel2) The above system can be realized in parallel form as shown in Figure. 51. What is the main disadvantage of direct-form realization? The direct-form realization is extremely sensitive to paramet When the order of the system NV is large, a small change im: due to parameter quantization, results in a large change in poles and zeros of the system. + es 52. Realize y(n) + y(n+1)+ Given y(n) + y(n 1) + Fuln ~2) = a(n) Taking z-transform on both sides Y(z) { +27 +32] = X(z) ; where Hy(z) = Ho(z) = m can be obtained by performing a Ledes— where {p,} are the poles — Pre ic uln— 2) =2(n) in ¥(2) AG) = a 1 1 Sz-) lto2Infinite Impulse Response Filters 5.117 33, What is the advantage of cascade realization? Quatization errors can be minimized if we realize form. an LTI system in cascade