MATH 8_QUARTER 4

WEEK 1
Name:___________________________ Grade and Section_______

Illustrating Theorems on Triangle Inequalities

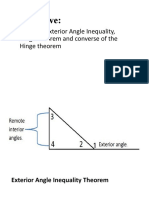
Exterior Angle Inequality Theorem. This theorem states that the measure of any exterior angle of a
triangle is greater than both non-adjacent interior angles or remote interior angles. In the figure below,
∠JBP > ∠JOB
∠JBP > ∠OJB
Triangle Inequality Theorem. This theorem states that the sum of lengths of two sides of the triangle will
always be greater than the length of the third side. In the figure below,
𝐴𝐵̅̅ +𝐵𝐶̅ ̅̅ > 𝐴𝐶̅̅
𝐴𝐶̅̅̅ + 𝐵𝐶̅̅̅ > 𝐴𝐵̅̅̅
𝐴𝐵̅̅ + 𝐴𝐶̅̅ > 𝐵𝐶̅̅
Hinge Theorem. This theorem states that if two triangles have two congruent sides, then the one with the
larger included angle has the longer third side.
𝐴𝐵̅̅ ≅ 𝐷𝐸̅̅
𝐴𝐶̅̅ ≅ 𝐷𝐹̅̅
𝐵𝐶̅̅̅ < 𝐸𝐹̅̅̅
∠A < ∠D
Converse of the Hinge Theorem. Given that two sides of one triangle are congruent to two sides of a second
triangle. If the third side of the first triangle is longer than the third side of the second triangle, then the included
angle of the first triangle is larger than the included angle of the second triangle.

Activity.
Exercise 1: Fact or Bluff
Identify the following statements if correct or not. If the statement is correct write FACT and BLUFF if
otherwise on the space before each item.
________ 1. ∠4 > ∠2
________ 2. ∠1 > ∠4
________ 3. ∠4 > ∠3
________ 4. 𝑋𝑌 ̅̅+ 𝑋𝑍̅̅̅ > 𝑌𝑍̅̅̅
________ 5. 𝑌𝑍̅̅ + 𝑋𝑍̅̅ < 𝑋𝑌