Real Analysis

Grinshpan

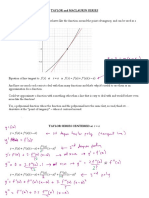
Peano and Lagrange remainder terms

Theorem. Let f be defined about x = x0 and be n times differentiable at x0 , n ≥ 1.

Form the nth Taylor polynomial of f centered at x0 ,
n
f (k) (x0 )
Tn (x) = ∑ (x − x0 )k .
k=0 k!
Then
f (x) − Tn (x)
lim = 0.
x→x0 (x − x0 )n

One says that the order of tangency of f and Tn at x = x0 is higher than n,

and writes f (x) = Tn (x) + o((x − x0 )n ) as x → x0 (Landau’s little-o notation).
The remainder f (x) − Tn (x) = o((x − x0 )n ), x → x0 , is said to be in Peano’s form.
Proof. By assumption, r(x) = f (x) − Tn (x) is differentiable (n − 1) times
in a neighborhood of x0 , has nth derivative at x0 , and satisfies
r(x0 ) = r′ (x0 ) = . . . = r(n) (x0 ) = 0.
In light of l’Hôpital’s rule (applied (n − 1) times), it suffices to show that
r(n−1) (x)
lim = 0.
x→x0 n!(x − x0 )

The latter condition holds because r(n−1) (x0 ) = r(n) (x0 ) = 0. ◻

Theorem. Let f be n times continuously differentiable on the interval [x0 , x], and
let f (n+1) exist in the open interval (x0 , x). Then, for some c ∈ (x0 , x),
f (n+1) (c)
f (x) = Tn (x) + (x − x0 )n+1 .
(n + 1)!
f (n+1) (c)
The remainder f (x) − Tn (x) = (x − x0 )n+1 is said to be in Lagrange’s form.
(n + 1)!
Proof. The remainder r = f − Tn satisfies r(x0 ) = r′ (x0 ) = . . . = r(n) (x0 ) = 0.
So, applying Cauchy’s mean value theorem (n + 1) times, we produce a monotone
sequence of numbers x1 ∈ (x0 , x), x2 ∈ (x0 , x1 ), . . . , xn+1 ∈ (x0 , xn ) such that
r(x) r′ (x1 ) r′′ (x2 ) r(n+1) (xn+1 )
= = = . . . = .
(x − x0 )n+1 (n + 1)(x1 − x0 )n (n + 1)n(x2 − x0 )n−1 (n + 1)!
The conclusion now follows by setting c = xn+1 and noting that r(n+1) (c) = f (n+1) (c). ◻

The Taylor remainder f (x) − Tn (x) about x0 can also be written in the Cauchy form
(x − c)n x (x − s)n
f (n+1) (c) (x − x0 ) (Ex 6.6.9) and integral form ∫ f (n+1) (s) ds (Ex 8.3.9).
n! x0 n!