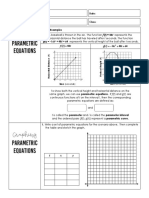
Differentiate on a component-by-component basis to obtain

𝑟 ′ (𝑡) = 𝑖 + 2𝑡 𝑗

From the position vector r(t), parametric equations 𝑥 = 𝑡 𝑎𝑛𝑑 𝑦 = 𝑡 + 2

The corresponding rectangular position is 𝑦 = 𝑥 2 + 2

When t = 1, r(1) = i+3j and 𝑟 ′ (𝑡) = 𝑖 + 2𝑡 𝑗

6
5
4
3

1 x

-3 -2
y y
-1 y
1 2 3 y

The parametrization of the curve represented by the vector-valued function

𝑟(𝑡) = 𝑓(𝑡)𝑖 + 𝑔(𝑡)𝑗 + ℎ(𝑡)𝑘
is smooth on an open interval I if f’ , g’ , and h’ are continuous on I and r’(t) ≠ 0 for any value of t in
the interval I.