! " Textbook Solutions Expert Q&A Practice NEW!

Find solutions for your homework Search

home / study / engineering / civil engineering / building materials and theory of constructions / building materials and
theory of constructions solutions manuals / principles of geotechnical engineering / 9th edition / chapter 10 / problem 3p

Principles of Geotechnical Engineering (9th Edition)

See this solution in the app

Chapter 10, Problem 3P 10 Bookmarks Show all steps: ON

Post a question
Answers from our experts for your tough
homework questions
Problem
Enter question

Using the principles of Mohr’s circles for the soil element

Next
shown in Figure 10.36, determine the following: Continue to post
a. Maximum and minimum principal stresses 20 questions remaining

b. Normal and shear stresses on plane AB Snap a photo from your

phone to post a question
We'll send you a one-time
download link

Step-by-step solution
888-888-8888 Text me
By providing your phone number, you agree to receive
Step 1 of 9 a one-time automated text message with a link to get
the app. Standard messaging rates may apply.

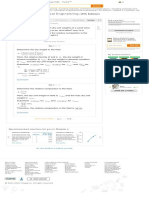
Consider the standard element as follows:

My Textbook Solutions

Principles of... Mechanics of Mechanics of

Materials Materials
9th Edition 8th Edition 7th Edition

View all solutions

Chegg tutors who can help

right now

S
Rensselaer Polytec… 1465

Alfredo
Rasmussen College 372

Hannah
Brigham Young Uni… 1013

Find me a tutor

Comment

Step 2 of 9

Consider the standard element as follows:

On comparing with standard element:

Comment

Step 3 of 9

Plot the Mohr circle with given stresses.

Construct a circle with the two points.

Comment

Step 4 of 9

(a)
The point where the circle touches the normal stress axis are
the principle stresses.

Comment

Step 5 of 9

(b)
To find the stresses on plane AB, rotate the connecting line
by , the stresses on the new location are the normal and
shear stresses on plane AB.

Comment

Step 6 of 9

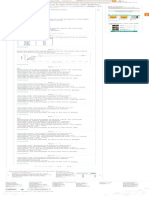
Calculation of stresses through Mohr’s circle formulas:

(a)
Calculate maximum principle stress using the following
relation:

Here, the maximum principle stress is , the normal stresses

along x and y-axis is and respectively, and shearing
stress is .
Substitute for , for , and for .

Therefore, the maximum principle stress is .

Comment

Step 7 of 9

Calculate minimum principle stress using the following

relation:

Here, the minimum principle stress is .

Substitute for , for , and for .

Therefore, the minimum principle stress is .

Comment

Step 8 of 9

(b)
Calculate the normal stress on the plane AB by using the
following relation:

Here, the angle made with major principal plane is .

Substitute for , for , for , and
for .

Therefore, normal stress on plane the AB is .

Comments (1)

Step 9 of 9

Calculate the shear stress on the plane AB by using the

following relation:

Substitute for , for , for , and

for .

Therefore, shear stress on the plane is .

Comment

Was this solution helpful? 8 0

Recommended solutions for you in Chapter 10

Chapter 10, Problem 22P Chapter 10, Problem 21P

Refer to Figure 10.49. Refer to Figure 10.48. If R = 4 m and hw = height of

For the linearly increasing water = 5 m, determine the vertical stress increases
vertical loading on an 2 m below the loaded area at radial distances
infinite strip of width 5 m, where r = 0, 2, 4, 6, and 8 m.
determine the vertical...
See solution
See solution

See more problems in subjects you study

ABOUT CHEGG LEGAL & POLICIES CHEGG PRODUCTS AND SERVICES CHEGG NETWORK CUSTOMER SERVICE
Become a Tutor Advertising Choices Cheap Textbooks Online Tutoring EasyBib Customer Service
Chegg For Good Cookie Notice Chegg Coupon Sell Textbooks Internships.com Give Us Feedback
College Marketing General Policies Chegg Play Solutions Manual Studyblue Help with Chegg Tutors
Corporate Development Intellectual Property Chegg Study Help Study 101 Thinkful Help with eTextbooks
Investor Relations Rights College Textbooks Test Prep Help to use EasyBib Plus
Jobs Terms of Use eTextbooks Textbook Rental Manage Chegg Study
Join Our Affiliate Program Chegg Tutors Terms of Chegg Math Solver Used Textbooks Subscription
Service Return Your Books
Media Center Mobile Apps Digital Access Codes
Global Privacy Policy Textbook Return Policy
Site Map
DO NOT SELL MY INFO
Honor Code

© 2003-2020 Chegg Inc. All rights reserved.