subsection

Search Wikipedia Create account Log in

subsection
functions

Taylor series
convergence

64 languages
andcommon

Contents [hide] Article Talk Read Edit View history Tools

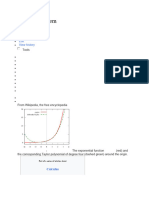
(Top) From Wikipedia, the free encyclopedia

some
subsection
error

Definition
of

In mathematics, the Taylor series or Taylor expansion

Approximation
subsection
series

Examples of a function is an infinite sum of terms that are

series

expressed in terms of the function's derivatives at a

Maclaurin

History
single point. For most common functions, the function
variables
ofTaylor

Analytic functions
Toggle

and the sum of its Taylor series are equal near this
of

Approximation error and point. Taylor series are named after Brook Taylor, who
List
several
Calculation

convergence introduced them in 1715. A Taylor series is also called a

Toggle

List of Maclaurin series of Maclaurin series when 0 is the point where the
series in

some common functions derivatives are considered, after Colin Maclaurin, who
Toggle

Calculation of Taylor series made extensive use of this special case of Taylor series
Toggle Taylor

in the mid-18th century.

Taylor series as definitions
The partial sum formed by the first n + 1 terms of a
Taylor series in several Taylor series is a polynomial of degree n that is called
variables
the nth Taylor polynomial of the function. Taylor
Comparison with Fourier polynomials are approximations of a function, which As the degree of the Taylor polynomial rises, it
series become generally better as n increases. Taylor's approaches the correct function. This image shows
sin x and its Taylor approximations by polynomials of
See also theorem gives quantitative estimates on the error degree 1, 3, 5, 7, 9, 11, and 13 at x = 0.
introduced by the use of such approximations. If the
Notes
Taylor series of a function is convergent, its sum is the
References Part of a series of articles about
limit of the infinite sequence of the Taylor polynomials. A
Calculus
External links function may differ from the sum of its Taylor series, even if its
Fundamental theorem
Taylor series is convergent. A function is analytic at a point x if it
Limits · Continuity
is equal to the sum of its Taylor series in some open interval (or Rolle's theorem · Mean value theorem ·
open disk in the complex plane) containing x. This implies that Inverse function theorem
the function is analytic at every point of the interval (or disk).
Differential [show]

Integral [show]
Definition [ edit ]
Series [hide]
The Taylor series of a real or complex-valued function f (x) that Geometric (arithmetico-geometric) · Harmonic
is infinitely differentiable at a real or complex number a is the · Alternating · Power · Binomial · Taylor
power series Convergence tests
Summand limit (term test) · Ratio · Root ·
Integral · Direct comparison ·
Limit comparison · Alternating series ·
Cauchy condensation · Dirichlet · Abel

Vector [show]

Multivariable [show]

Advanced [show]

Specialized [show]

Miscellaneous [show]

V·T·E

where n! denotes the factorial of n. In the more compact sigma notation, this can be written as

where f (n)(a) denotes the nth derivative of f evaluated at the point a. (The derivative of order zero of f is
defined to be f itself and (x − a)0 and 0! are both defined to be 1.)
With a = 0, the Maclaurin series takes the form:[1]

or in the compact sigma notation:

Examples [ edit ]

The Taylor series of any polynomial is the polynomial itself.

1
The Maclaurin series of 1 − x is the geometric series

So, by substituting x for 1 − x, the Taylor series of 1x at a = 1 is

By integrating the above Maclaurin series, we find the Maclaurin series of ln(1 − x), where ln denotes the
natural logarithm:

The corresponding Taylor series of ln x at a = 1 is

and more generally, the corresponding Taylor series of ln x at an arbitrary nonzero point a is:

The Maclaurin series of the exponential function ex is

The above expansion holds because the derivative of ex with respect to x is also ex, and e0 equals 1. This
leaves the terms (x − 0)n in the numerator and n! in the denominator of each term in the infinite sum.

History [ edit ]

The ancient Greek philosopher Zeno of Elea considered the problem of summing an infinite series to achieve
a finite result, but rejected it as an impossibility;[2] the result was Zeno's paradox. Later, Aristotle proposed a
philosophical resolution of the paradox, but the mathematical content was apparently unresolved until taken
up by Archimedes, as it had been prior to Aristotle by the Presocratic Atomist Democritus. It was through
Archimedes's method of exhaustion that an infinite number of progressive subdivisions could be performed to
achieve a finite result.[3] Liu Hui independently employed a similar method a few centuries later.[4]

In the 14th century, the earliest examples of specific Taylor series (but not the general method) were given by
Madhava of Sangamagrama.[5][6] Though no record of his work survives, writings of his followers in the Kerala
school of astronomy and mathematics suggest that he found the Taylor series for the trigonometric functions
of sine, cosine, and arctangent (see Madhava series). During the following two centuries his followers
developed further series expansions and rational approximations.

In late 1670, James Gregory was shown in a letter from John Collins several Maclaurin series (
and ) derived by Isaac Newton, and told that Newton had developed a general method for
expanding functions in series. Newton had in fact used a cumbersome method involving long division of
series and term-by-term integration, but Gregory did not know it and set out to discover a general method for
himself. In early 1671 Gregory discovered something like the general Maclaurin series and sent a letter to
Collins including series for (the integral of ), (the
integral of sec, the inverse Gudermannian function), and (the
Gudermannian function). However, thinking that he had merely redeveloped a method by Newton, Gregory
never described how he obtained these series, and it can only be inferred that he understood the general
method by examining scratch work he had scribbled on the back of another letter from 1671.[7]

In 1691–1692, Isaac Newton wrote down an explicit statement of the Taylor and Maclaurin series in an
unpublished version of his work De Quadratura Curvarum. However, this work was never completed and the
relevant sections were omitted from the portions published in 1704 under the title Tractatus de Quadratura
Curvarum.

It was not until 1715 that a general method for constructing these series for all functions for which they exist
was finally published by Brook Taylor,[8] after whom the series are now named.

The Maclaurin series was named after Colin Maclaurin, a professor in Edinburgh, who published the special
case of the Taylor result in the mid-18th century.

Analytic functions [ edit ]

Main article: Analytic function

If f (x) is given by a convergent power series in an open

disk centred at b in the complex plane (or an interval in
the real line), it is said to be analytic in this region. Thus
for x in this region, f is given by a convergent power
series

Differentiating by x the above formula n times, then

setting x = b gives:

and so the power series expansion agrees with the 2

The function e(−1/x ) is not analytic at x = 0: the
Taylor series. Thus a function is analytic in an open disk
Taylor series is identically 0, although the function is
centered at b if and only if its Taylor series converges to not.
the value of the function at each point of the disk.

If f (x) is equal to the sum of its Taylor series for all x in the complex plane, it is called entire. The polynomials,
exponential function ex, and the trigonometric functions sine and cosine, are examples of entire functions.
Examples of functions that are not entire include the square root, the logarithm, the trigonometric function
tangent, and its inverse, arctan. For these functions the Taylor series do not converge if x is far from b. That
is, the Taylor series diverges at x if the distance between x and b is larger than the radius of convergence.
The Taylor series can be used to calculate the value of an entire function at every point, if the value of the
function, and of all of its derivatives, are known at a single point.

Uses of the Taylor series for analytic functions include:

1. The partial sums (the Taylor polynomials) of the series can be used as approximations of the function.
These approximations are good if sufficiently many terms are included.
2. Differentiation and integration of power series can be performed term by term and is hence particularly
easy.
3. An analytic function is uniquely extended to a holomorphic function on an open disk in the complex
plane. This makes the machinery of complex analysis available.
4. The (truncated) series can be used to compute function values numerically, (often by recasting the
polynomial into the Chebyshev form and evaluating it with the Clenshaw algorithm).
5. Algebraic operations can be done readily on the power series representation; for instance, Euler's
formula follows from Taylor series expansions for trigonometric and exponential functions. This result
is of fundamental importance in such fields as harmonic analysis.
6. Approximations using the first few terms of a Taylor series can make otherwise unsolvable problems
possible for a restricted domain; this approach is often used in physics.

Approximation error and convergence [ edit ]

Main article: Taylor's theorem

Pictured is an accurate approximation of sin x around

the point x = 0. The pink curve is a polynomial of
degree seven:

The error in this approximation is no more than |x|9 / 9!.

For a full cycle centered at the origin (−π < x < π) the
error is less than 0.08215. In particular, for −1 < x < 1,
the error is less than 0.000003.

In contrast, also shown is a picture of the natural

logarithm function ln(1 + x) and some of its Taylor The sine function (blue) is closely approximated by
its Taylor polynomial of degree 7 (pink) for a full period
polynomials around a = 0. These approximations
centered at the origin.
converge to the function only in the region −1 < x ≤ 1;
outside of this region the higher-degree Taylor
polynomials are worse approximations for the function.

The error incurred in approximating a function by its nth-

degree Taylor polynomial is called the remainder or
residual and is denoted by the function Rn(x). Taylor's
theorem can be used to obtain a bound on the size of
the remainder.

In general, Taylor series need not be convergent at all.

And in fact the set of functions with a convergent Taylor
series is a meager set in the Fréchet space of smooth
functions. And even if the Taylor series of a function f
does converge, its limit need not in general be equal to
the value of the function f (x). For example, the function

The Taylor polynomials for ln(1 + x) only provide

accurate approximations in the range −1 < x ≤ 1. For
is infinitely differentiable at x
= 0, and has all derivatives x > 1, Taylor polynomials of higher degree provide
worse approximations.
zero there. Consequently, the Taylor series of f (x)
about x = 0 is identically zero. However, f (x) is not the
zero function, so does not equal its Taylor series around
the origin. Thus, f (x) is an example of a non-analytic
smooth function.

In real analysis, this example shows that there are

infinitely differentiable functions f (x) whose Taylor
series are not equal to f (x) even if they converge. By
contrast, the holomorphic functions studied in complex
analysis always possess a convergent Taylor series,
and even the Taylor series of meromorphic functions,
which might have singularities, never converge to a
value different from the function itself. The complex The Taylor approximations for ln(1 + x) (black). For
−1/z2 x > 1, the approximations diverge.
function e , however, does not approach 0 when z
approaches 0 along the imaginary axis, so it is not
continuous in the complex plane and its Taylor series is undefined at 0.

More generally, every sequence of real or complex numbers can appear as coefficients in the Taylor series of
an infinitely differentiable function defined on the real line, a consequence of Borel's lemma. As a result, the
radius of convergence of a Taylor series can be zero. There are even infinitely differentiable functions defined
on the real line whose Taylor series have a radius of convergence 0 everywhere.[9]

A function cannot be written as a Taylor series centred at a singularity; in these cases, one can often still
achieve a series expansion if one allows also negative powers of the variable x; see Laurent series. For
2
example, f (x) = e−1/x can be written as a Laurent series.

Generalization [ edit ]

There is, however, a generalization[10][11] of the Taylor series that does converge to the value of the function
itself for any bounded continuous function on (0,∞), using the calculus of finite differences. Specifically, one
has the following theorem, due to Einar Hille, that for any t > 0,

n
Here Δh is the nth finite difference operator with step size h. The series is precisely the Taylor series, except
that divided differences appear in place of differentiation: the series is formally similar to the Newton series.
When the function f is analytic at a, the terms in the series converge to the terms of the Taylor series, and in
this sense generalizes the usual Taylor series.

In general, for any infinite sequence ai, the following power series identity holds:

So in particular,

The series on the right is the expectation value of f (a + X), where X is a Poisson-distributed random variable
j
that takes the value jh with probability e−t/h· (t/h) . Hence,
j!

The law of large numbers implies that the identity holds.[12]

List of Maclaurin series of some common functions [ edit ]

See also: List of mathematical series

Several important Maclaurin series expansions follow.[13] All these expansions are valid for complex
arguments x.

Exponential function [ edit ]

The exponential function (with base e) has Maclaurin series

It converges for all x.

The exponential generating function of the Bell numbers is the

exponential function of the predecessor of the exponential function:

Natural logarithm [ edit ]

Main article: Mercator series

The natural logarithm (with base e) has Maclaurin series

The exponential function ex (in blue),
and the sum of the first n + 1 terms of
its Taylor series at 0 (in red).

They converge for . (In addition, the series for ln(1 − x) converges for x = −1, and the series for
ln(1 + x) converges for x = 1.)

Geometric series [ edit ]

The geometric series and its derivatives have Maclaurin series

All are convergent for . These are special cases of the binomial series given in the next section.

Binomial series [ edit ]

The binomial series is the power series

whose coefficients are the generalized binomial coefficients

(If n
= 0, this product is an empty product and has value 1.) It converges for for any real or complex
number α.

When α = −1, this is essentially the infinite geometric series mentioned in the previous section. The special
1 1
cases α = 2 and α = − 2 give the square root function and its inverse:

When only the linear term is retained, this simplifies to the binomial approximation.

Trigonometric functions [ edit ]

The usual trigonometric functions and their inverses have the following Maclaurin series:

All angles are expressed in radians. The numbers Bk appearing in the expansions of tan x are the Bernoulli
numbers. The Ek in the expansion of sec x are Euler numbers.

Hyperbolic functions [ edit ]

The hyperbolic functions have Maclaurin series closely related to the series for the corresponding
trigonometric functions:

The numbers Bk appearing in the series for tanh x are the Bernoulli numbers.

Polylogarithmic functions [ edit ]

The polylogarithms have these defining identities:

The Legendre chi functions are defined as follows:

And the formulas presented below are called inverse tangent integrals:

In statistical thermodynamics these formulas are of great importance.

Elliptic functions [ edit ]

The complete elliptic integrals of first kind K and of second kind E can be defined as follows:

The Jacobi theta functions describe the world of the elliptic modular functions and they have these Taylor
series:

The regular partition number sequence P(n) has this generating function:

The strict partition number sequence Q(n) has that generating function:

Calculation of Taylor series [ edit ]

Several methods exist for the calculation of Taylor series of a large number of functions. One can attempt to
use the definition of the Taylor series, though this often requires generalizing the form of the coefficients
according to a readily apparent pattern. Alternatively, one can use manipulations such as substitution,
multiplication or division, addition or subtraction of standard Taylor series to construct the Taylor series of a
function, by virtue of Taylor series being power series. In some cases, one can also derive the Taylor series
by repeatedly applying integration by parts. Particularly convenient is the use of computer algebra systems to
calculate Taylor series.

First example [ edit ]

In order to compute the 7th degree Maclaurin polynomial for the function

one may first rewrite the function as

The Taylor series for the natural logarithm is (using the big O notation)

and for the cosine function

The latter series expansion has a zero constant term, which enables us to substitute the second series into
the first one and to easily omit terms of higher order than the 7th degree by using the big O notation:

Since the cosine is an even function, the coefficients for all the odd powers x, x3, x5, x7, ... have to be zero.

Second example [ edit ]

Suppose we want the Taylor series at 0 of the function

We have for the exponential function

and, as in the first example,

Assume the power series is

Then multiplication with the denominator and substitution of the series of the cosine yields

Collecting the terms up to fourth order yields

The values of can be found by comparison of coefficients with the top expression for , yielding:

Third example [ edit ]

Here we employ a method called "indirect expansion" to expand the given function. This method uses the
known Taylor expansion of the exponential function. In order to expand (1 + x)ex as a Taylor series in x, we
use the known Taylor series of function ex:

Thus,

Taylor series as definitions [ edit ]

Classically, algebraic functions are defined by an algebraic equation, and transcendental functions (including
those discussed above) are defined by some property that holds for them, such as a differential equation. For
example, the exponential function is the function which is equal to its own derivative everywhere, and
assumes the value 1 at the origin. However, one may equally well define an analytic function by its Taylor
series.

Taylor series are used to define functions and "operators" in diverse areas of mathematics. In particular, this is
true in areas where the classical definitions of functions break down. For example, using Taylor series, one
may extend analytic functions to sets of matrices and operators, such as the matrix exponential or matrix
logarithm.

In other areas, such as formal analysis, it is more convenient to work directly with the power series
themselves. Thus one may define a solution of a differential equation as a power series which, one hopes to
prove, is the Taylor series of the desired solution.

Taylor series in several variables [ edit ]

The Taylor series may also be generalized to functions of more than one variable with[14][15]

For example, for a function that depends on two variables, x and y, the Taylor series to second order
about the point (a, b) is

where the subscripts denote the respective partial derivatives.

Second-order Taylor series in several variables [ edit ]

See also: Linearization § Multivariable functions

A second-order Taylor series expansion of a scalar-valued function of more than one variable can be written
compactly as

where D f (a) is the gradient of f evaluated at x = a and D2 f (a) is the Hessian matrix. Applying the multi-
index notation the Taylor series for several variables becomes

which is to be understood as a still more abbreviated multi-index version of the first equation of this
paragraph, with a full analogy to the single variable case.

Example [ edit ]

In order to compute a second-order Taylor series expansion around

point (a, b) = (0, 0) of the function

one first computes all the necessary partial derivatives:

Second-order Taylor series

approximation (in orange) of a
function f (x,y) = ex ln(1 + y)
around the origin.

Evaluating these derivatives at the origin gives the Taylor coefficients

Substituting these values in to the general formula

produces

Since ln(1 + y) is analytic in |y| < 1, we have

Comparison with Fourier series [ edit ]

Main article: Fourier series

The trigonometric Fourier series enables one to express a periodic function (or a function defined on a closed
interval [a,b]) as an infinite sum of trigonometric functions (sines and cosines). In this sense, the Fourier
series is analogous to Taylor series, since the latter allows one to express a function as an infinite sum of
powers. Nevertheless, the two series differ from each other in several relevant issues:

The finite truncations of the Taylor series of f (x) about the point x = a are all exactly equal to f at a. In
contrast, the Fourier series is computed by integrating over an entire interval, so there is generally no
such point where all the finite truncations of the series are exact.
The computation of Taylor series requires the knowledge of the function on an arbitrary small
neighbourhood of a point, whereas the computation of the Fourier series requires knowing the function on
its whole domain interval. In a certain sense one could say that the Taylor series is "local" and the Fourier
series is "global".
The Taylor series is defined for a function which has infinitely many derivatives at a single point, whereas
the Fourier series is defined for any integrable function. In particular, the function could be nowhere
differentiable. (For example, f (x) could be a Weierstrass function.)
The convergence of both series has very different properties. Even if the Taylor series has positive
convergence radius, the resulting series may not coincide with the function; but if the function is analytic
then the series converges pointwise to the function, and uniformly on every compact subset of the
convergence interval. Concerning the Fourier series, if the function is square-integrable then the series
converges in quadratic mean, but additional requirements are needed to ensure the pointwise or uniform
convergence (for instance, if the function is periodic and of class C1 then the convergence is uniform).
Finally, in practice one wants to approximate the function with a finite number of terms, say with a Taylor
polynomial or a partial sum of the trigonometric series, respectively. In the case of the Taylor series the
error is very small in a neighbourhood of the point where it is computed, while it may be very large at a
distant point. In the case of the Fourier series the error is distributed along the domain of the function.

See also [ edit ]

Asymptotic expansion
Generating function
Laurent series
Madhava series
Newton's divided difference interpolation
Padé approximant
Puiseux series
Shift operator

Notes [ edit ]

1. ^ Thomas & Finney 1996, §8.9

2. ^ Lindberg, David (2007). The Beginnings of Western Science (2nd ed.). University of Chicago Press. p. 33.
ISBN 978-0-226-48205-7.
3. ^ Kline, M. (1990). Mathematical Thought from Ancient to Modern Times . New York: Oxford University Press.
pp. 35 –37. ISBN 0-19-506135-7.
4. ^ Boyer, C.; Merzbach, U. (1991). A History of Mathematics (Second revised ed.). John Wiley and Sons.
pp. 202–203 . ISBN 0-471-09763-2.
5. ^ "Neither Newton nor Leibniz – The Pre-History of Calculus and Celestial Mechanics in Medieval Kerala"
(PDF). MAT 314. Canisius College. Archived (PDF) from the original on 2015-02-23. Retrieved 2006-07-09.
6. ^ S. G. Dani (2012). "Ancient Indian Mathematics – A Conspectus". Resonance. 17 (3): 236–246.
doi:10.1007/s12045-012-0022-y . S2CID 120553186 .
7. ^ Turnbull, Herbert Westren, ed. (1939). James Gregory; Tercentenary Memorial Volume. G. Bell & Sons.
pp. 168–174.

Roy, Ranjan (1990). "The Discovery of the Series Formula for π by Leibniz, Gregory and Nilakantha" (PDF).
Mathematics Magazine. 63 (5): 291–306. doi:10.1080/0025570X.1990.11977541 .

Malet, Antoni (1993). "James Gregorie on Tangents and the "Taylor" Rule for Series Expansions". Archive for
History of Exact Sciences. 46 (2): 97–137. doi:10.1007/BF00375656 . JSTOR 41133959 .
8. ^ Taylor, Brook (1715). Methodus Incrementorum Directa et Inversa [Direct and Reverse Methods of
Incrementation] (in Latin). London. p. 21–23 (Prop. VII, Thm. 3, Cor. 2). Translated into English in Struik, D. J.
(1969). A Source Book in Mathematics 1200–1800 . Harvard University Press. pp. 329–332. ISBN 978-0-674-
82355-6. Re-translated into English by Ian Bruce (2007) as Methodus Incrementorum Directa & Inversa ,
17centurymaths.com.

Feigenbaum, L. (1985). "Brook Taylor and the method of increments". Archive for History of Exact Sciences. 34
(1–2): 1–140. doi:10.1007/bf00329903 .
9. ^ Rudin, Walter (1980), Real and Complex Analysis, New Delhi: McGraw-Hill, p. 418, Exercise 13, ISBN 0-07-
099557-5
10. ^ Feller, William (2003) [1971]. An introduction to probability theory and its applications. Vol. 2 (3rd ed.). Wiley.
pp. 230–2. ISBN 9789971512989. OCLC 818811840 .
11. ^ Hille, Einar; Phillips, Ralph S. (1957), Functional analysis and semi-groups, AMS Colloquium Publications,