Table II

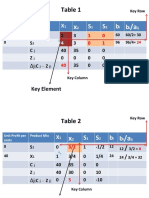
Cj 60 50 0 0 100

Prod Qty X y S1 S2 A1
50 Y 3 3/5 1 1/5 0 0
Replacing
100 A1 row

ZJ
CJ - ZJ

To compute for the A1, Zj, and Cj - Zj row entries, follow the same process in simplex
maximization problem. These entries are shown in Table 2 with complete entries below.

Table II (with complete entries)

Cj 60 50 0 0 100

Prod Qty X y S1 S2 A1
50 Y 3 3/5 1 1/5 0 0

100 A1 4 8/5 0 -4/5 -1 1

Pivot row
ZJ 550 190 50 -70 -100 100
CJ - ZJ -130 0 70 100 0

Optimum
column

Again, choose the most negative entry in the last row. Negative one hundred thirty (-130)
being the most negative should be encircled. Then locate the pivotal row by dividing 3 by 3/5 and 4 by
8/5. Since 4 ÷ 8/5 has the smallest quotient which is 2.5, then A1 row is the pivotal row. To find the
replacing row, divide the entries in the pivot row by the pivot entry which is 8/5.

Table III with replacing row

 Cj 60 50 0 0 100

Prod Qty X y S1 S2 A1
50 Y

60 X 5/2 1 0 -1/2 -5/8 5/8

ZJ
CJ - ZJ

Repeat the process and place the complete entries in Table III

Cj 60 50 0 0 100

Prod Qty X y S1 S2 A1
50 Y 3/2 0 1 1/3 3/8 -3/8

60 X 5/2 1 0 -1/2 -5/8 5/8

ZJ 225 60 50 -5 -75/4 75/4

CJ - ZJ 0 0 5 75/4 325 /4

Since there is no more negative entry in the last row, the table is optimum. Hence the decision
are as follows:

X = 5/2, Y = 3/2, Minimum Z = 225