1

Semester -3
EE 3101
Introduction to system theory
Lecture : 9
DISTRIBUTION THEORY AND FOURIER TRANSFORM OF SOME SPECIAL FUNCTIONS


















Compiled by:
Sakshi Mishra: BE/1239/09
Abhishek Koul: BE/1242/09
Prateek Tripathi: BE/1237/09


2






























3


1. GATE FUNCTION
A unit gate function is defined as a gate pulse of unit height and unit width,centered at the origin
0 |t| > T
Rect(
t
/
2T
) = {
1
/
2
|t| = T

1 |t| < T
Here ,the function exists as a pulse for a duration of 2T seconds. The inverse of factor of variable t
indicates the width of the pulse. In the given figure,the width is 2T.





2. SINC FUNCTION



4


The sinc function sinc(x), also called the "sampling function," is a function that arises frequently in signal
processing and the theory of Fourier transform. It is also known as filtering or interpolating function. The full
name of the function is "sine cardinal," but it is commonly referred to by its abbreviation, "sinc." There are two
definitions in common use. The one adopted in this work defines

a. sinc(x) is an even function of x.

b. Sinc (x) = 0 when sin(x) = 0 except at x = 0.

c. Using LHospital rule

Lim sin(x) / x = Lim cos(x) = 1
x0 x0


d. This has the normalization

-

+
sinc(x)dx =







The half-infinite integral of sinc(x) can be derived using contour integration. In the above figure, consider the
path =
1
+
12
+
2
+
21
Now write z = Re
i
. On an arc, dz = iRe
i
and on the x-axis, dz = e
i
dR. Write
-

+
sinc(x)dx = I (e
i
/z) dz

5

where I denotes the imaginary part. Now define
The same result is arrived at using the method of complex residues by noting
I = 0 +
1
/
2

(2i Res f(z) )
= i (z 0) (e
iz
/ z) |
z = 0
= i e
iz
|
z =0

= i
Since the integrand is symmetric , we have
0

+
sinc(x)dx = /2
This is an improper integral.
We thus have the following result:


6


But the expression on the right, considered as a function of k, is the sign function. We have here one of the
simplest examples of an integral representation of a function; the need for such a representation often arises in
applied mathematics. The integral on the left is known as Dirichlets discontinuity factor.





3. TRANSFORM OF GATE AND SINC FUNCTIONS

a. TRANSFORM OF GATE FUNCTION



7






b. TRANSFORM OF SINC FUNCTION

f(x) = sinc(x)
Then
F(j) =

sinc(t).e
jt
dt
=

(sin(at)/at). e
jt
dt
=

( sin(at).cos(t)dt )/at
I =(
1
/
2a
)

(sin(t + at).dt )/t +

II (
1
/
2a
)

(sin(t - at).dt )/t

=(

/
2a
) rect(
t
/
2a
)


8


c. BANDWIDTH OF RECT(
t
/
2T
)

The spectrum F() peaks at = 0 and decays at higher frequencies. Therefore rect(
t
/
2T
) is a
lowpass signal with most of the signal energy concentrated in lower frequency components. But ,
because the spectrum exists for t = . However , much of the spectrum is concentrated within the
first lobe. Therefore , a rough estimate of the bandwidth is 2T

d. WINDOWED SINC FILTER

In signal processing, a sinc filter is an idealized filter that removes all frequency components
above a given bandwidth, leaves the low frequencies alone, and has linear phase. The filter's
impulse response is a sinc function in the time domain, and its frequency response is a rectangular
function.


9

It is an "ideal" low-pass filter in the frequency sense, perfectly passing low frequencies, perfectly
cutting all the frequencies.
Real-time filters can only approximate this ideal, since an ideal sinc filter (aka rectangular filter)
acausal and produces infinite delay.

Windowed-sinc filters are used to separate one band of frequencies from another. They are very
stable, produce few surprises, and can be pushed to incredible performance levels. These
exceptional frequency domain characteristics are obtained at the expense of poor performance in
the time domain, including excessive ripple and overshoot in the step response. When carried out
Convolving an input signal with this filter kernel provides a perfect low-pass
filter. The problem is, the sinc function continues to both negative and positive
infinity without dropping to zero amplitude. While this infinite length is not
a problem for mathematics
To get around this problem, we will make two modifications to the sinc
function in (b), resulting in the waveform shown in (c). First, it is truncated
to M%1 points, symmetrically chosen around the main lobe, where M is an
even number. All samples outside these M%1 points are set to zero, or simply
ignored. Second, the entire sequence is shifted to the right so that it runs from
0 to M. This allows the filter kernel to be represented using only positive
indexes. While many programming languages allow negative indexes, they are
a nuisance to use. The sole effect of this M/2 shift in the filter kernel is to
shift the output signal by the same amount.
Since the modified filter kernel is only an approximation to the ideal filter
kernel, it will not have an ideal frequency response. To find the frequency
response that is obtained, the Fourier transform can be taken of the signal in
(c), resulting in the curve in (d). It's a mess! There is excessive ripple in the
passband and poor attenuation in the stopband (recall the Gibbs effect
discussed in Chapter 11). These problems result from the abrupt discontinuity
at the ends of the truncated sinc function. Increasing the length of the filter
kernel does not reduce these problems; the discontinuity is significant no matter
how long M is made.
Fortunately, there is a simple method of improving this situation. Figure (e)
shows a smoothly tapered curve called a Blackman window. Multiplying the
truncated-sinc, (c), by the Blackman window, (e), results in the windowedsinc
filter kernel shown in (f). The idea is to reduce the abruptness of the
truncated ends and thereby improve the frequency response. Figure (g) shows
this improvement. The passband is now flat, and the stopband attenuation is
so good it cannot be seen in this graph.
Several different windows are available, most of them named after their
original developers in the 1950s. Only two are worth using, the Hamming
window and the Blackman window These are given by:




10




Figure 16-2a shows the shape of these two windows for M 50 (i.e., 51 total points in the curves).
Which of these two windows should you use? It's a trade-off between parameters. As shown in
Fig. 16-2b, the Hamming window has about a 20% faster roll-off than the Blackman. However, (c)
shows that the Blackman has a better stopband attenuation. To be exact,the stopband attenuation
for the Blackman is -74dB (-0.02%), while theHamming is only -53dB (-0.2%). Although it
cannot be seen in these graphs,the Blackman has a passband ripple of only about 0.02%, while the
Hamming is typically 0.2%. In general, the Blackman should be your first choice; a
slow roll-off is easier to handle than poor stopband attenuation.There are other windows you
might hear about, although they fall short of theBlackman and Hamming. The Bartlett window is
a triangle, using straight lines for the taper. The Hanning window, also called the raised cosine
window, is given by: w[i] 0.5& 0.5 cos(2Bi /M) . These two windows have about the same roll-
off speed as the Hamming, but worse stopband attenuation (Bartlett: -25dB or 5.6%, Hanning -
44dB or 0.63%). You might also hear on a rectangular window. This is the same as no window,
just a truncation of the tails (such as in Fig. 16-1c). While the roll-off is -2.5 times faster than the
Blackman, the stopband attenuation is only -21dB (8.9%).

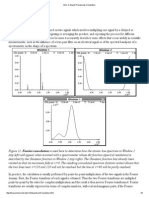
FIGURE 16-1
Derivation of the windowed-sinc filter kernel. The frequency response of the ideal low-pass filter is shown
in (a), with the corresponding filter kernel in (b), a sinc function. Since the sinc is infinitely long, it must be
truncated to be used in a computer, as shown in (c). However, this truncation results in undesirable changes
in the frequency response, (d). The solution is to multiply the truncated-sinc with a smooth window, (e),
resulting in the windowed-sinc filter kernel, (f). The frequency response of the windowed-sinc, (g), is smooth
and well behaved. These figures are not to scale.

11



12

FIGURE 16-2
Characteristics of the Blackman and Hamming
windows. The shapes of these two windows are
shown in (a), and given by Eqs. 16-1 and 16-2. As
shown in (b), the Hamming window results in about
20% faster roll-off than the Blackman window.
However, the Blackman window has better stopband
attenuation (Blackman: 0.02%, Hamming:
0.2%), and a lower passband ripple (Blackman:
0.02% Hamming: 0.2%).






4. DISTRIBUTION THEORY

Distribution states the relation between following improper integrals



13



a. Lim
-

(sin(t)/) = (t)
t

b.
-

cos(t) d = ()


c.
0

sin(t) () =
1
/
t


d.
0

sin(t) dt =
1
/

Lim
-

(sin(t)/) = (t)
t
In the above expression, the number of oscillations per unit length of the sinc function approaches
infinity. Nevertheless, the expression always oscillates inside an envelope of 1/(t), and
approaches zero for any nonzero value of x. This complicates the informal picture of (t) as being
zero for all x except at the point x = 0 and illustrates the problem of thinking of the delta function
as a function rather than as a distribution.

-

cos(t) d = ()





Fourier transform


}

= dt e t t
t je
o o ) ( )] ( [ F 1
0
= =
=

t
t j
e
e

14




] 1 [ ) (
1
=F t o e
t
e
d e
t j
}

= 1
2
1
e
t
e
d e
t j
}

=
2
1

15






5. FOURIER TRANSFORM OF FUNCTIONS USING DISTRIBUTION THEORY

a. Fourier transform of constant


b. Fourier transform of exponential wave e
jt





c. Fourier transform of sinusoidal functions
Using the exponential wave fourier transform and eulers theorem,we get







e
t
o
e
d e t
t j
}

=
2
1
) ( e e e
t
d t j t ) sin (cos
2
1
}

+ =
} }

+ = e e
t
e e
t
td
j
td sin
2
cos
2
1
}

=
0
cos
1
e e
t
td
e e
e
d Ae A j F
t j
}

= = ] [ ) ( F |
.
|

\
|
=
}

dt e A
t j ) (
2
1
2
e
t
t ) ( 2 e o tA =
) ( 2 ] 1 [ e to = F
) ( 2 ] [
0
0
e e to
e
=
t j
e F
) ( ) ( cos
0 0 0
e e to e e to e + +
F
t
) ( ) ( sin
0 0 0
e e to e e to e + + j j t
F

16







d. Fourier transform of unit step function

F(u(t)) =
0

e
-jt
dt

=
0

cos(t)dt -
0

sin(t)dt

= () +
1
/
j








17





e. Fourier transform of periodic function
We can express a periodic function as







The FT of a periodic function consists of a sequence of equidistant impulses located at the harmonic
frequencies of the function.



T
e c t f
n
t jn
n
t
e
e
2
, ) (
0
0
= =

=
(

= =

= n
t jn
n
e c t f j F
0
)] ( [ ) (
e
e F F

=
=
n
t jn
n
e c ] [
0
e
F

=
=
n
n
n c ) ( 2
0
e e to

=
=
n
n
n c ) ( 2
0
e e o t

18







6. FOURIER TRANSFORM OF NON PERIODIC FUNCTION

a. f(t)=unit step function[u(t)]

F(jw)= ()

-jwt
(dt)
or,F(jw)= ()

-jwt
(dt)
=

-jwt
(dt) [using u(t)=1]
= () ()

Using distribution theory, ()

=1/w & () ()

=(w)-j/w
=(w)+1/jw



19





b. f(t)=signum function[sgn(t)]
Sgn(t)=-1 ,t<0
+1,t>0
F(jw)= ()

-jwt
(dt)
or,F(jw)= ()

-jwt
(dt)+ ()

-jwt
(dt)
=

-jwt
(dt)+

-jwt
(dt) [using the definition of the function]
=

jwt
(dt) +

-jwt
(dt)
= (

-jwt
-e
jwt
)(dt)
= ()()

=-2j () ()

20

Using distribution theory, ()

=1/w
=-2j/w
=2/wj
Since,signum function is odd, fourier transform is completely imaginary.



c. TRUNCATED SINUSOID
f(t)=cos(w
c
t).u(t)
F(jw)= ()

-jwt
(dt)
or,F(jw)= ()

cos(w
c
t)e
-jwt
(dt)
=1/2 ()

{e
jw1t
+e
-jw1t
}e
-jwt
(dt)
=1/2 ()

[e
jt(w1-w)
+e
-jt(w+w1)
](dt)
=1/2{ ()

e
-jt(w-w1)
(dt)+ ()

e
-jt(w+w1)
}
=1/2[(w w
c
)+ (w +w
c
)]+1/2{1/j(w-w
c
)+1/j(w+w
c
)}
=/2[(w w
c
)+ (w +w
c
)]+jw/(w
c
2
-w
2
)