Law of Sine

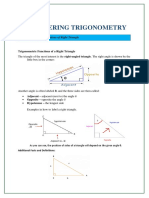
The Law of Sines states that:

In any given triangle, the ratio of the length of a side and the sine of the angle opposite that side
is a constant.

The following figure shows the Law of Sines for the triangle A, B, and C

The a, b, and c are the lengths of the side of the triangle and A, B, and C are their respective
opposite angles of the triangle.

Formula of sine in trigonometry can be given as:

sin A sin B sin C

= =
a b c

The Law of Sines is also known as the sine rule, sine law, or sine formula. It is valid for all types
of triangles: right, acute or obtuse triangles.

The Law of Sines can be used to compute the remaining sides of a triangle when two angles
and a side are known (AAS or ASA) or when we are given two sides and a non-enclosed angle
(SSA).

We can use the Law of Sines when solving triangles. Solving a triangle means to find the
unknown lengths and angles of the triangle.

Proof of sine rule

Theorem: In any triangle,side are proportional to ine of opposite angles

sin A/a = sin B/b = sin C/c

Given: triangle A, B, and C

We can have 2types of triangle, the triangle 1 and triangle 2

To prove:
Law of Cosines
The law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles.
Using trigonometry, we can now obtain values of distances and angles which cannot be
measured otherwise. The law of cosines finds application while computing the third side of a
triangle given two sides and their enclosed angle, and for computing the angles of a triangle if
all three sides are known to us. (A triangle has 6 elements, 3 sides + 3 angles).

The law of cosine states that the square of any one side of a triangle is equal to the difference
between the sum of squares of the other two sides and double the product of other sides and
cosine angle included between them.

Let a, b, and c be the lengths of the three sides of a triangle and A, B, and C be the three
angles of the triangle.

The law of cosine formula can be given as:

a2= b2 + c2 - 2bc (cos A)

b2 = c2 + a2 - 2ca (cos B)

c2 = a2 + b2 - 2ab (cos C)

To prove: