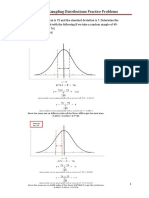
F.Y.B.Sc COMPUTER SCIENCE: PRACTICAL NO.

02
PROBLEMS BASED ON NORMAL DISTRIBUTION
DATE: –/–/2022

1. X is a normally normally distributed variable with mean μ = 30 and standard

deviation σ = 4. Find
a) P(x < 40)
b) P(x > 21)c) P(30 < x < 35)
2. Assume that the test scores of a college entrance exam fits a normal distribution.
Furthermore, the mean test score is 72, and the standard deviation is 15.2. What
is the percentage of students scoring 84 or more in the exam?
3. Suppose a random variable X is normally distributed and the mean of X is 12 and
S.D. is 4, find the probability of the following:
(a) (i) 𝑋 ≥ 20
(ii) 𝑋 ≤ 20 and
(iii) 0 ≤ 𝑋 ≤ 12
(b) Find x if P(X > x) = 0.24

(c) Find x0 and x1 when P(x0 < X < x1) = 0.50 and P(X > x1 ) = 0.25

4. X is a random variable with mean 30 and S.D. 5. Find the probabilities that
(i) 26 ≤ 𝑋 ≤ 40
(ii) 𝑋 ≥ 45
(iii) |𝑋 − 30| > 5
5. The length of human pregnancies from conception to birth approximates a normal
distribution with a mean of 266 days and a standard deviation of 16 days. What
proportion of all pregnancies will last between 240 and 270 days (roughly between
8 and 9 months)? What length of time marks the shortest 70% of all pregnancies?
6. Find the 87th percentile for X where X~N (4.11,1.372).
7. Most graduate schools of business require applicants for admission to take the
Graduate Management Admission Council’s GMAT examination. Scores on the
GMAT are roughly normally distributed with a mean of 527 and a standard
deviation of 112. What is the probability of an individual scoring above 500 on the
GMAT?