Swk, MAT-120, 3.

8 Local Linear Approximation; Differentials

Linear Approximations

In this section we’re going to take a look at an application not of derivatives but of the tangent line to a
function. Of course, to get the tangent line we do need to take derivatives, so in some way this is an
application of derivatives as well. Given a function f(x) we can find its tangent at x=a.

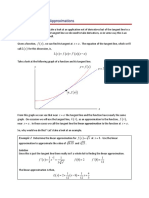
Take a look at the following graph of a function and its tangent line.

From this graph we can see that near x=a the tangent line and the function have nearly the same
graph. Sometimes we will use the tangent line, L(x), as an approximation to the function, f(x), near
x=a. In these cases we call the tangent line the linear approximation to the function at x=a.

Dr. Showkat Page 1 3/21/24

 Swk, MAT-120, 3.8 Local Linear Approximation; Differentials

So, why do we do this? Let’s take a look at an example.

Determine the linear approximation for at x=8. Use the linear approximation to
approximate the value of and .

Solution Since this is just the tangent line there really isn’t a whole lot to finding the linear
approximation.

Dr. Showkat Page 2 3/21/24

 Swk, MAT-120, 3.8 Local Linear Approximation; Differentials

The linear approximation is then,

Now, the approximations are nothing more than plugging these into the linear approximation.

So, at x=8.05 this linear approximation does a very good job of approximating the actual value. However,
at x=25 it doesn’t do such a good job.

Linear approximations do a very good job of approximating values of f(x) “near” x=a. However, the farther
away from x=a we get the worse the approximation is liable to be. Note as well that how near we need to
stay to x=a for a good approximation will depend upon the function and x=a that we’re using.

Dr. Showkat Page 3 3/21/24

 Swk, MAT-120, 3.8 Local Linear Approximation; Differentials

Determine the linear approximation for at

Solution Again, there really isn’t a whole lot to this example.

So, as long as θis small we can say that

Dr. Showkat Page 4 3/21/24

 Swk, MAT-120, 3.8 Local Linear Approximation; Differentials
Differentials:
In this section we’re going to introduce a notation and look at an application of this new notation. Given a
function y=f(x) we call dx and dy differentials and the relationship between them is given by,

There is a nice application to differentials. If we think of as the change in x then

is the change in y corresponding to the change in x. Now, if is small we can assume that
.

Compute dy and if as x changes from x=2.0 to x=2.03.

Solution First let’s compute the change in y.

Dr. Showkat Page 5 3/21/24

 Swk, MAT-120, 3.8 Local Linear Approximation; Differentials
Now let’s get the formula for dy.

Next if we have x=2 and we assume that then,

So, we can see that in fact provided we keep small.

Let . Find and at x=4 with Then make a sketch of , showing and in
the sketch.

A sphere was measured and its radius was found to be 45 inches with a possible error of no
more than 0.01 inches. What is the maximum possible error in the volume if we use this value of
the radius?
Solution First, recall the equation for the volume of a sphere.

Now, if we start with r=45 and use then should give us maximum
error.
So, first get the formula for the differential.

Now compute dV.

The maximum error in the volume is then 254.46 in3.

Be careful to not assume this is a large error. On the surface it looks large, however if we compute the
actual volume for r=45 we get V=381703.51 in3. So, in comparison this isn’t all that large!

Exercise-3.8, Assignment Problems # 1 – 12 (Odd), 19 – 54 (Odd).

a) Find the local linear approximation of f(x)=x 1/2 at x0=1

b) Use local linear approximation obtained in part (a) to approximate (1.1)1/2
Find the differential if (a) (b)
Use a differential to approximate the change in revenue R corresponding to an increase in the
number of sales x of one unit, if and

Dr. Showkat Page 6 3/21/24