Professional Documents
Culture Documents
L36 37 Chapter 16 Enhanced Control Strategies
L36 37 Chapter 16 Enhanced Control Strategies
Uploaded by
website.techfestOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
L36 37 Chapter 16 Enhanced Control Strategies
L36 37 Chapter 16 Enhanced Control Strategies
Uploaded by
website.techfestCopyright:
Available Formats
Process Control CL 302
Prof. Bharat Suthar
Department of Chemical Engineering
IIT Bombay, Mumbai, India, 400076
Lecture 36
Chapter#16
Enhanced Single-Loop Control Strategies
bharat.k.suthar[at]iitb.ac.in
Landline: +91 (22) 2576 7243
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 1
Admin:
❑ Total 5 contact hours becore DX grade
❑ Including one quiz
❑ Histogram of attendance
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 2
Chapter 16
Enhanced Single-Loop
Control Strategies
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 3
Outline
❑ Cascade Control
❑ Time-Delay Compensation
❑ Inferential Control
❑ Nonlinear Control Systems
❑ Adaptive Control Systems
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 4
Cascade Control
❑ Drawback of FB Control for the 100th times:
❖ Corrective action only after CV is disturbed.
❑ What are the options here?
❖ FF Control
➢ Requires measurement of disturbances
➢ Requires process model to get to the control law.
❖ Alternative:
➢ Use secondary FB controller using secondary measurement point
➢ What is secondary measurement point?
➢ It can recognize the upset sooner than CV, disturbance is not necessary measured.
➢ Example?
➢ This approach is called cascade control.
❑ Cascade Control:
❖ Useful when the disturbances are in the MV itself
❖ Final control element exhibits nonlinear behavior
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 5
Example: Exothermic Chemical Reactor
❖ DV#1: Reactor feed temp and composition
❖ DV#2: Cooling water temperature
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 6
Example:
❑ Natural Draft Furnace
❖ Case 1: disturbance in the oil flow rate.
❖ Case 2: Disturbance in the fuel gas pressure (disturbance is associated with
MV)
➢ Corrective action only occurs after the temp of the oil changes (sluggish response)
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 7
Example:
❑ Conventional FB Cascade Controller
❖ Primary (master) Control loop (TT and TC)
❖ Secondary (slave) Control loop (PT and PC)
❖ Provide improved response because the
pressure can be adjusted back quickly.
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 8
Cascade Control
❑ Features:
❖ Two FB controllers
➢ Single control valve
❖ Output signal of the "master"
controller is the set-point for “slave"
controller.
❖ Two FB control loops are "nested"
with the "slave" (or "secondary")
control loop inside the "master" (or
"primary") control loop.
❑ Terminology:
❖ Slave vs. master
❖ Secondary vs. primary
❖ Inner vs. outer
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 9
Cascade Control: Block Diagram
❑ Onenote: Block Diagram:
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 10
Draw Block Diagram
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 11
Block diagram
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 12
Onenote:
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 13
Block Diagram Algebra
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 14
Stability of Cascade Control
❑ Same Char. Polynomial:
❑ If inner loop is removed (𝐺𝑐2 = 1, 𝐺𝑚2 = 0):
❖ Same as that for conventional feedback control (1 + 𝐺𝑂𝐿 = 0)
❖ If inner loop is faster in response and takes care of disturbance quicker:
➢ The stability of the system will improve (i.e. one can use larger value of 𝐾𝑐1 in the
outer loop)
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 15
Example: Comparison
❑ Conventional FB: Char. Eq. ❑ Cascade Control (char Eq)
➢ 𝐺𝑐2 = 1, 𝐺𝑚2 = 0 ❖
5 5 4
➢ 1 + 𝐺𝑐1 𝐺𝑣 𝐺𝑝2 𝐺𝑝1 𝐺𝑚1 = 0 ❖ 1 + 𝐾𝑐2 𝑠+1 0.2 + 𝐾𝑐1 𝐾𝑐2 𝑠+1 ∙ 1 ∙ (4𝑠+1)(2𝑠+1) ∙ 0.05 = 0
➢
5 4
1 + 𝐾𝑐1 𝑠+1 × 1 × (4𝑠+1)(2𝑠+1) × 0.05 = 0 ➢ If 𝐾𝑐2 = 4
❑ Routh table: ❑ Routh table:
❑ Stability range for Kc1 ❑ Stability range for Kc1
➢ −1 < 𝐾𝑐1 < 11.25 ❖ −1.25 < 𝐾𝑐1 < 43.3
➢ Larger range of 𝐾𝑐1 possible.
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 16
Quickness of response:
𝑌2 𝑌2
❑ Lets take ❑ Lets take in cascade control
𝑌෨𝑠𝑝2 𝑌෨𝑠𝑝2
❖ Without inner loop: ❖ With Inner Loop
➢ Same as 𝐺𝑣 𝐺𝑝2 𝑌2 4∙
5
∙1
➢ Since 𝐺𝑐2 = 1, 𝐺𝑚2 = 0 ❖ = 𝑠+1
5
𝑌෨𝑠𝑝2 1+4∙𝑠+1∙1∙0.2
5
➢ 𝐺𝑣 𝐺𝑝2 = 𝑌 4
𝑠+1 ❖ 𝑌෨ 2 = 0.2𝑠+1
➢ Time constant 1 min 𝑠𝑝2
➢ Time constant 0.2 min
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 17
Simulink Exercise:
Cascade Control
Conventional PI Control
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 18
Simulink Results: D1 vs D2 effect
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 19
Outline
❑ Cascade Control
❑ Time-Delay Compensation
❑ Inferential Control
❑ Nonlinear Control Systems
❑ Adaptive Control Systems
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 20
Process Control CL 302
Prof. Bharat Suthar
Department of Chemical Engineering
IIT Bombay, Mumbai, India, 400076
Lecture 36
Chapter#16
Enhanced Single-Loop Control Strategies
bharat.k.suthar[at]iitb.ac.in
Landline: +91 (22) 2576 7243
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 21
Outline
❑ Cascade Control
❑ Time-Delay Compensation
❑ Inferential Control
❑ Nonlinear Control Systems
❑ Adaptive Control Systems
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 22
Time Delay Compensation
❑ Example: 16.2
❑ Compare the set-point responses for
a second-order process with a time
delay (min) and without the delay.
𝑒 −𝜃𝑠
❑ 𝐺𝑝 = , 𝐺𝑚 = 𝐺𝑣 = 1
(5𝑠+1)(3𝑠+1)
❖ PI Controller w/o time delay 𝜃 = 0
➢ 𝐾𝑐 = 3.02 and 𝜏𝐼 = 6.5 min
❖ PI Controller with time delay 𝜃 ≠ 0
➢ 𝐾𝑐 = 1.23 and 𝜏𝐼 = 7 min Time delay of 2 min give rise to significant
➢ Gain is reduced to meet stability sluggishness in the response.
criteria
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 23
Closer look at time delay processes
Controller action calculated Controller action calculated Process with delay
but not implemented and implemented (no delay)
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 24
Smith’s Predictor:
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 25
Error Signal in Smith’s predictor
❑ What is 𝐸 ′
❖ 𝐸 ′ = 𝑌𝑠𝑝 − (𝑌 − 𝑌෨2 ) − 𝑌෨1
❖ If plant model mismatch is
not there
➢ 𝑌 = 𝑌෨2
❖ 𝐸 ′ = 𝑌𝑠𝑝 − 𝑌෨1
❑ For this ideal case, the
controller responds to the
error signal that would occur
if no time delay were present
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 26
Comparison to conventional FB
❑ Conventional FB ❑ FB + Smith’s Predictor
𝑌 𝐺𝑐 (𝐺 ∗ 𝑒 −𝜃𝑠 ) 𝑌 𝐺𝑐 (𝐺 ∗ 𝑒 −𝜃𝑠 )
= =
𝑌𝑠𝑝 1 + 𝐺𝑐 ( 𝐺 ∗ 𝑒 −𝜃𝑠 ) 𝑌𝑠𝑝 1 + 𝐺𝑐 𝐺 ∗
𝐺𝑝
𝐸′ = 𝑌𝑠𝑝 − 𝑌 (Has Time delay) 𝐸′ = 𝑌𝑠𝑝 − 𝑌෨1 (No time delay)
Theoretical advantage of eliminating
the time delay from the characteristic equation,
provide process model is reasonably accurate
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 27
Performance of Smith’s Predictor
Conventional FB Conventional FB + Smith’s Predictor
𝑒 −𝜃𝑠
𝐺𝑝 =
(5𝑠 + 1)(3𝑠 + 1)
For 𝜃 = 0, 𝐾𝑐 = 3.02, 𝜏𝐼 = 6.5
For 𝜃 = 1, 𝐾𝑐 = 1.23, 𝜏𝐼 = 7
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 28
Simulink Exercise
❑ What happens if plant model mismatch is there?
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 29
Performance of Smith’s Predictor:
Disturbance rejection
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 30
Outline
❑ Cascade Control
❑ Time-Delay Compensation
❑ Inferential Control
❑ Nonlinear Control Systems
❑ Adaptive Control Systems
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 31
Inferential Control
❑ Problem:
❖ Controlled variable cannot be measured or has large sampling period.
❑ Possible solutions:
❖ Control a related variable
➢ (e.g., temperature instead of composition).
❖ Inferential control: Control is based on an estimate of the controlled variable.
➢ The estimate is based on available measurements.
➢ Examples: empirical relation, Kalman filter
❑ Modern term: soft sensor
❖ Using the mathematical modeling
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 32
Temp. control instead of composition control
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 33
Inferential Control
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 34
Outline
❑ Cascade Control
❑ Time-Delay Compensation
❑ Inferential Control
❑ Nonlinear Control Systems
❖ Self read
❑ Adaptive Control Systems
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 35
Adaptive Control
❑ A general control strategy for control problems where the process or
operating conditions can change significantly and unpredictably.
❖ Example:
➢ Catalyst decay
➢ equipment fouling (change in equipment characteristics)
➢ Ambient variations (rain storm, daily cycles)
❖ Many different types of adaptive control strategies have been proposed.
❑ Self-Tuning Control (STC):
❖ A very well-known strategy and probably the most widely used adaptive
control strategy.
❖ Basic idea: STC is a model-based approach.
❖ As process conditions change, update the model parameters by using least
squares estimation and recent input and output (𝑢 & 𝑦) data.
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 36
Adaptive Control: Self Tuning Method
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 37
Outline
❑ Cascade Control
❑ Time-Delay Compensation
❑ Inferential Control
❑ Nonlinear Control Systems
❖ Self read
❑ Adaptive Control Systems
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 38
Takeaway Points/Summary
❑ We have studied a number of control strategies that offer the potential of
enhanced performance over what can be achieved with conventional
single-loop PID controllers.
❖ How to efficiently handle disturbances in MV
➢ Cascade control
❖ How to handle time delay in the process
➢ Smith’s predictor
❖ How to handle processes where the CV measurement is not available online
➢ Iinferential control
❖ How to handle processes that undergo changes
➢ Adaptive control
❑ Overall, the idea that process models can be effectively used to improve
the control performance is instilled.
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 39
Reference:
❑ Process Dynamics and Control (Seborg, Edgar, Mellichamp, Doyle III)
❑ Process Control Designing Processes and Control Systems for Dynamic
Performance: Thomas E. Marlin
CL 302 | Bharat Suthar | Process Control | IIT Bombay, Mumbai, India 40
You might also like
- MIXED - USE - BUILDING - AhmedDocument46 pagesMIXED - USE - BUILDING - AhmedTeferi81% (57)
- Marketing Strategies and Plan Reaction PaperDocument2 pagesMarketing Strategies and Plan Reaction PaperRocel NavajaNo ratings yet
- Process Dynamics and ControlDocument31 pagesProcess Dynamics and ControlKim Joon sung100% (1)
- Process Control Instrumentation Technology 8th EdDocument62 pagesProcess Control Instrumentation Technology 8th EdSaeed AshaNo ratings yet
- L38 39 Chapter 18 MultiLoop and MultiVarDocument62 pagesL38 39 Chapter 18 MultiLoop and MultiVarkarthikNo ratings yet
- L25 26 27 Chapter 11Document50 pagesL25 26 27 Chapter 11karthikNo ratings yet
- L34 35 Chapter 15Document45 pagesL34 35 Chapter 15website.techfestNo ratings yet
- Os Assignment 28.12.2021Document21 pagesOs Assignment 28.12.2021Tapan KumarNo ratings yet
- PID Tuning MethodsDocument52 pagesPID Tuning Methodsarash esfahanNo ratings yet
- Lecture-5 - Classification of Process Variables - Control StrategiesDocument18 pagesLecture-5 - Classification of Process Variables - Control StrategiesKshitij SoniNo ratings yet
- CH 2Document48 pagesCH 2Endalew kassahunNo ratings yet
- Feedback Controller TuningDocument23 pagesFeedback Controller Tuningso cool100% (1)
- Design of Feedback Controllers Controller TuningDocument39 pagesDesign of Feedback Controllers Controller TuningAthiradh R NNo ratings yet
- Advanced Control StrategiesDocument58 pagesAdvanced Control StrategiesAthiradh R NNo ratings yet
- Pres06 MNG512 (111 - 112) Control ActionsDocument37 pagesPres06 MNG512 (111 - 112) Control ActionsMahmudul HasanNo ratings yet
- Advanced Control Seborg Chapter 15 16Document43 pagesAdvanced Control Seborg Chapter 15 16Akhil Tiwari0% (1)
- Control Station PT37 - Loop Tuning - Eliminating The Guesswork of Tuning PID ControllersDocument38 pagesControl Station PT37 - Loop Tuning - Eliminating The Guesswork of Tuning PID ControllersIsaac MendibleNo ratings yet
- Controller TuningDocument54 pagesController TuningNikhil SinghNo ratings yet
- ChE170 Lecture 9 (Control Tuning) PDFDocument27 pagesChE170 Lecture 9 (Control Tuning) PDFRowieNo ratings yet
- What To CNTRLDocument12 pagesWhat To CNTRLramanjorewal786No ratings yet
- A Review of Tuning Method For Cascade ControlDocument9 pagesA Review of Tuning Method For Cascade Control賴明宏No ratings yet
- PPC Textbook PDFDocument289 pagesPPC Textbook PDFPepe LuisNo ratings yet
- Chapter 1 Introduction To Process ControlDocument40 pagesChapter 1 Introduction To Process ControlHoàngNo ratings yet
- PID Control - KeyDocument50 pagesPID Control - KeyHaozhi LiNo ratings yet
- College of Engineering and TechnologyDocument27 pagesCollege of Engineering and TechnologyAbdeta TerfaNo ratings yet
- Position Control of DC Motor Using Genetic Algorithm Based PID ControllerDocument35 pagesPosition Control of DC Motor Using Genetic Algorithm Based PID ControllerSarat Chandra100% (1)
- Process Reaction Curve PDFDocument6 pagesProcess Reaction Curve PDFVikalp SagarNo ratings yet
- Pipelining: CIT 595 Spring 2007Document16 pagesPipelining: CIT 595 Spring 2007kumar07xNo ratings yet
- CH4404 Lecture 00 ModuleIntroductionDocument25 pagesCH4404 Lecture 00 ModuleIntroductionRRNo ratings yet
- Class III Mecha.Document23 pagesClass III Mecha.yodahe aberaNo ratings yet
- PURE PresentationDocument34 pagesPURE PresentationRadha LahotiNo ratings yet
- Accuracy Versus ResolutionDocument3 pagesAccuracy Versus ResolutionPablo BertoloneNo ratings yet
- An124 Tuning Control Loops With The IMC Tuning Method PDFDocument3 pagesAn124 Tuning Control Loops With The IMC Tuning Method PDFSyed Mian Fahim KakakhailNo ratings yet
- PDC OverviewDocument13 pagesPDC OverviewVardhan KaushikNo ratings yet
- Practical Process Control Textbook 20060612 PDFDocument296 pagesPractical Process Control Textbook 20060612 PDFMuhammad SabihNo ratings yet
- Introduction OnkeshDocument12 pagesIntroduction OnkeshPatricia JosephNo ratings yet
- Control and Modelling of Bioprocesses: Slides Adapted From Dr. Katie ThirdDocument54 pagesControl and Modelling of Bioprocesses: Slides Adapted From Dr. Katie ThirdNitin KhodifadNo ratings yet
- Lecture1 PDFDocument9 pagesLecture1 PDFLokesh JenaNo ratings yet
- DS+PC 6Document8 pagesDS+PC 6Sebastian BalceroNo ratings yet
- L8 Process SynchronizationDocument29 pagesL8 Process Synchronizationpuja1002.hrNo ratings yet
- CMOS Testing-2: Design and Test Flow: Old ViewDocument16 pagesCMOS Testing-2: Design and Test Flow: Old Viewprathap_somaNo ratings yet
- 13 Cascade ControlDocument39 pages13 Cascade ControlMansour AbdulazizNo ratings yet
- Pressure Buildup and Horner PlotDocument46 pagesPressure Buildup and Horner PlotKAORU AmaneNo ratings yet
- 4 - Pillar Three-20170305Document129 pages4 - Pillar Three-20170305Ahmad100% (1)
- Chapter 6 CD Qualtiy ControlDocument46 pagesChapter 6 CD Qualtiy ControlEngineerMqNo ratings yet
- Enpm808J Rehabilitation Robotics Lecture #3 Anindo Roy, PHDDocument103 pagesEnpm808J Rehabilitation Robotics Lecture #3 Anindo Roy, PHDRahul Subramonian BamaNo ratings yet
- 2019-Control of Four Tank System Using Model Predictive ControllerDocument5 pages2019-Control of Four Tank System Using Model Predictive ControllerAravindan MohanNo ratings yet
- Experiment No: 6 Date: 24-09-2021: Aim: To Perform The Cascade Control Scheme. TheoryDocument7 pagesExperiment No: 6 Date: 24-09-2021: Aim: To Perform The Cascade Control Scheme. TheoryDrumil PatelNo ratings yet
- Lecture 9Document31 pagesLecture 9yuzlubahadirNo ratings yet
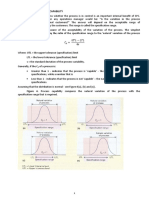
- Process CapabilityDocument4 pagesProcess CapabilityLeonardo SanchezNo ratings yet
- 05 Process SynchronizationDocument11 pages05 Process SynchronizationRaza AhmadNo ratings yet
- LCS 11th Lab SlidesDocument21 pagesLCS 11th Lab Slidesareebarajpoot0453879No ratings yet
- Control Inrtroduction ADocument48 pagesControl Inrtroduction Arhm 018No ratings yet
- Process Dynamics and Control: CHE302, Fall 2001 Professor Dae Ryook YangDocument29 pagesProcess Dynamics and Control: CHE302, Fall 2001 Professor Dae Ryook YangTewodros MathewosNo ratings yet
- Routh-Hurwitz Stability CriterionDocument37 pagesRouth-Hurwitz Stability CriterionNagajyothiVirivintiNo ratings yet
- Part 3: Regulatory ( Stabilizing ) Control: Inventory (Level) Control StructureDocument63 pagesPart 3: Regulatory ( Stabilizing ) Control: Inventory (Level) Control StructuretahermohNo ratings yet
- 7 Design Root LocusDocument31 pages7 Design Root LocusDogukan KarabeyinNo ratings yet
- PLC Ladder Program Concept: Sameer S. Purao Plant Engg. (Inst)Document69 pagesPLC Ladder Program Concept: Sameer S. Purao Plant Engg. (Inst)Saheblal YadavNo ratings yet
- 0 1 PID Control Vs APC ControlDocument26 pages0 1 PID Control Vs APC ControlDevesh Pratap ChandNo ratings yet
- Lecture 9 - Control Modes 2023Document33 pagesLecture 9 - Control Modes 2023Mohamed SalaheldinNo ratings yet
- Building a Successful Board-Test StrategyFrom EverandBuilding a Successful Board-Test StrategyRating: 4 out of 5 stars4/5 (1)
- Dynamic Programming and Its Application to Optimal ControlFrom EverandDynamic Programming and Its Application to Optimal ControlNo ratings yet
- F2 Syllabus Overview: Created By: Global CGMA University and Academic Center of ExcellenceDocument93 pagesF2 Syllabus Overview: Created By: Global CGMA University and Academic Center of Excellencesike1977No ratings yet
- Contract With Bond TemplateDocument2 pagesContract With Bond TemplateJenny Zacarias100% (4)
- Ikea Pricing IMDocument22 pagesIkea Pricing IMThanhHoàiNguyễnNo ratings yet
- Implementation of 7 Core Principles of ISO 26000 (CSR) in Bangladesh: A Case Study On GrameenphoneDocument14 pagesImplementation of 7 Core Principles of ISO 26000 (CSR) in Bangladesh: A Case Study On GrameenphoneKamalakar KaramchetiNo ratings yet
- Feehan Investments Management CaseDocument13 pagesFeehan Investments Management Casesarthak mendirattaNo ratings yet
- Revalidation of Trust PDFDocument18 pagesRevalidation of Trust PDFAmal P TomyNo ratings yet
- The Following Table Gives Earnings Per Share Figures For TheDocument2 pagesThe Following Table Gives Earnings Per Share Figures For TheAmit PandeyNo ratings yet
- YPO MX AI - AI Powered Org - Adriana Gomes - FINALDocument48 pagesYPO MX AI - AI Powered Org - Adriana Gomes - FINALAndrea ReséndizNo ratings yet
- Advanced Tally MCQ Original - WatermarkDocument90 pagesAdvanced Tally MCQ Original - WatermarkVinod RathodNo ratings yet
- The Role of Business Strategy To Create A Competitive Advantage in The OrganizationDocument5 pagesThe Role of Business Strategy To Create A Competitive Advantage in The OrganizationCao Đào Minh AnhNo ratings yet
- Securities and Exchange Commission: Republic of The PhilippinesDocument5 pagesSecurities and Exchange Commission: Republic of The PhilippinesMarc Jian uyNo ratings yet
- Review of Literatureinformal Sectorstreet VendorsDocument4 pagesReview of Literatureinformal Sectorstreet Vendorsfvgczbcy100% (1)
- Assignment 1 - Lagon, Mon Carla - Sec 15Document3 pagesAssignment 1 - Lagon, Mon Carla - Sec 15moncarla lagonNo ratings yet
- Zeilhoch - Summer Internship ProgammeDocument5 pagesZeilhoch - Summer Internship Progammejeffrijose14No ratings yet
- Case StudyDocument5 pagesCase StudynanthamkNo ratings yet
- Exercise No.2Document4 pagesExercise No.2Jeane Mae BooNo ratings yet
- Entrepreneurship Chapter FiveDocument9 pagesEntrepreneurship Chapter FiveAbdirahman MohamedNo ratings yet
- Chapter 2 Company and Marketing StrategyDocument42 pagesChapter 2 Company and Marketing StrategyGenoso OtakuNo ratings yet
- Accounting Standard2Document24 pagesAccounting Standard2shajiNo ratings yet
- Financial PlanDocument16 pagesFinancial PlanEtchin Agcol AnunciadoNo ratings yet
- ACT InvoiceDocument2 pagesACT InvoiceSuresh KumarNo ratings yet
- Instagram and Facebook MarketingDocument6 pagesInstagram and Facebook Marketingaadarsh mahajanNo ratings yet
- Financial Accounting The Impact On Decision Makers 10th Edition Porter Solutions ManualDocument41 pagesFinancial Accounting The Impact On Decision Makers 10th Edition Porter Solutions Manualhildabacvvz100% (28)
- 3a PDFDocument70 pages3a PDFAlexandru ManeaNo ratings yet
- Mel Arthor QueditDocument2 pagesMel Arthor QueditMel Arthor QueditNo ratings yet
- Swot Analysis: Presented By:-Ankita Sapra Divya Kapoor Jasleen Kaur Shreya AgarwalDocument29 pagesSwot Analysis: Presented By:-Ankita Sapra Divya Kapoor Jasleen Kaur Shreya AgarwalShreya AgarwalNo ratings yet
- Form GST REG-06: Government of IndiaDocument3 pagesForm GST REG-06: Government of IndiaVishal BawaneNo ratings yet
- Billing Payment E-Visa Malik AbidDocument1 pageBilling Payment E-Visa Malik AbidtasikmeikewijayantiaNo ratings yet