CHAPTER 7

Optimal Risky Portfolios

INVESTMENTS | BODIE, KANE, MARCUS

McGraw-Hill/Irwin Copyright © 2011 by The McGraw-Hill Companies, Inc. All rights reserved.
 7-2

The Investment Decision

• Top-down process with 3 steps:
1. Capital allocation between the risky portfolio
and risk-free asset
2. Asset allocation across broad asset classes
3. Security selection of individual assets within
each asset class

INVESTMENTS | BODIE, KANE, MARCUS

 7-3

Diversification and Portfolio Risk

• Market risk
– Systematic or nondiversifiable

• Firm-specific risk
– Diversifiable or nonsystematic

INVESTMENTS | BODIE, KANE, MARCUS

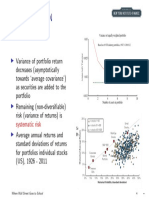
 7-4

Figure 7.1 Portfolio Risk as a Function of the

Number of Stocks in the Portfolio

INVESTMENTS | BODIE, KANE, MARCUS

 7-5

Figure 7.2 Portfolio Diversification

INVESTMENTS | BODIE, KANE, MARCUS

 7-6

Covariance and Correlation

• Portfolio risk depends on the
correlation between the returns of the
assets in the portfolio

• Covariance and the correlation

coefficient provide a measure of the
way returns of two assets vary

INVESTMENTS | BODIE, KANE, MARCUS

 7-7

Two-Security Portfolio: Return

rp  wr
D D
 wE r E
rP  Portfolio Return
wD  Bond Weight
rD  Bond Return
wE  Equity Weight
rE  Equity Return

E ( rp )  w D E ( rD )  w E E ( rE )

INVESTMENTS | BODIE, KANE, MARCUS

 7-8

Correlation Coefficients: Possible Values

Range of values for 1,2

+ 1.0 >  > -1.0
If = 1.0, the securities are perfectly
positively correlated
If = - 1.0, the securities are perfectly
negatively correlated

INVESTMENTS | BODIE, KANE, MARCUS

 7-9

Correlation Coefficients
• When ρDE = 1, there is no diversification

 P  wE E  wD D

• When ρDE = -1, a perfect hedge is possible

D
wE   1  wD
D  E

INVESTMENTS | BODIE, KANE, MARCUS

 7-10

Three-Asset Portfolio

E ( rp )  w1 E ( r1 )  w 2 E ( r2 )  w 3 E ( r3 )

 p2  w12 12  w22 22  w32 32

 2 w1w2 1, 2  2 w1w3 1,3  2 w2 w3 2,3

INVESTMENTS | BODIE, KANE, MARCUS

 7-11

Figure 7.3 Portfolio Expected Return as a

Function of Investment Proportions

INVESTMENTS | BODIE, KANE, MARCUS

 7-12

Figure 7.4 Portfolio Standard Deviation as

a Function of Investment Proportions

INVESTMENTS | BODIE, KANE, MARCUS

 7-13

The Minimum Variance Portfolio

• The minimum variance • When correlation is
portfolio is the portfolio less than +1, the
composed of the risky portfolio standard
assets that has the deviation may be
smaller than that of
smallest standard either of the individual
deviation, the portfolio component assets.
with least risk.
• When correlation is -
1, the standard
deviation of the
minimum variance
portfolio is zero.

INVESTMENTS | BODIE, KANE, MARCUS