Professional Documents
Culture Documents
Phy2 Lecture3 03
Phy2 Lecture3 03
Uploaded by
Muhammed Azeem RehmanOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Phy2 Lecture3 03
Phy2 Lecture3 03
Uploaded by
Muhammed Azeem RehmanCopyright:
Available Formats
Lecture 3
Ch16. Transverse Waves
University Physics: Waves and Electricity
Dr.-Ing. Erwin Sitompul
http://zitompul.wordpress.com
Announcements
Quiz 1
Next Week
From Lecture1 until Lecture3
Erwin Sitompul University Physics: Wave and Electricity 3/2
Homework 2: Phase Differences
A sinusoidal wave of frequency 500 Hz has a speed of 350 m/s.
(a) How far apart are two points that differ in phase by π/3
rad?
(b) What is the phase difference between two displacements
at a certain point at times 1 ms apart?
New
A sinusoidal wave of wavelength 280 cm has a speed of 60 m/s.
(a) How many seconds apart are two displacements at a
certain point that differ in phase by 2π/3 rad?
(b) What is the phase difference between two displacements
at a certain time at distances 14 cm apart?
Erwin Sitompul University Physics: Wave and Electricity 3/3
Solution of Homework 2: Phase Differences
f 500 Hz, v 350 m s
v 350
(a) 0.7 m
f 500
x 3
x (0.7) 0.117 11.7 cm
2 2 2
1 1
(b) T 0.002 s 2 ms
f 500
t t 1 ms
2 2 rad
T 2 T 2 ms
Erwin Sitompul University Physics: Wave and Electricity 3/4
Example I
A wave traveling along a string is described by
y(x,t) = 0.00327sin(72.1x–2.72t),
in which the numerical constants are in SI units.
(a) What is u, the transverse velocity of the element of the
string, at x = 22.5 cm and t = 18.9 s?
x 22.5 cm, t 18.9 s
y ( x, t ) (3.27 mm) sin(72.1x 2.72t )
y ( x, t )
u ( x, t )
t
(2.72 rad s)(3.27 mm) cos(72.1x 2.72t )
(8.894 mm s) cos(72.1x 2.72t )
u (0.225 m,18.9 s) ( 8.894 mm s) cos( 35.1855 rad)
7.197 mm s
Erwin Sitompul University Physics: Wave and Electricity 3/5
Example I
A wave traveling along a string is described by
y(x,t) = 0.00327sin(72.1x–2.72t),
in which the numerical constants are in SI units.
(b) What is the transverse acceleration ay of the same element
of the spring at that time?
x 22.5 cm, t 18.9 s
u ( x, t ) (8.894 mm s) cos(72.1x 2.72t )
u ( x, t )
a y ( x, t )
t
(2.72 rad s)(8.894 mm s) sin(72.1x 2.72t )
(24.192 mm s 2 ) sin(72.1x 2.72t )
a y (0.225 m,18.9 s) (24.192 mm s 2 ) sin( 35.1855 rad)
14.21mm s 2
Erwin Sitompul University Physics: Wave and Electricity 3/6
The Principle of Superposition for Waves
It often happens that two or more
waves pass simultaneously through
the same region (sound waves in a
concert, electromagnetic waves
received by the antennas).
Suppose that two waves travel
simultaneously along the same
stretched string, the displacement of
the string when the waves overlap is
then the algebraic sum.
Erwin Sitompul University Physics: Wave and Electricity 3/7
The Principle of Superposition for Waves
Let y1(x,t) and y2(x,t) be two waves travel simultaneously
along the same stretched string, then the displacement of the
string is given by:
y( x, t ) y1 ( x, t ) y2 ( x, t )
Overlapping waves algebraically add to produce a resultant
wave (or net wave).
Overlapping waves do not in any way alter the travel of each
other.
Erwin Sitompul University Physics: Wave and Electricity 3/8
Interference of Waves
Suppose there are two sinusoidal waves of the same
wavelength and the same amplitude, and they are moving in
the same direction, along a stretched string.
The resultant wave depends on the extent to which one wave
is shifted from the other.
We call this phenomenon of combining waves as
interference.
y1 ( x, t ) ym sin(kx t )
y2 ( x, t ) ym sin(kx t )
Erwin Sitompul University Physics: Wave and Electricity 3/9
Interference of Waves
The resultant wave as the superposition of y1(x,t) and y2(x,t) of
the two interfering waves is:
y( x, t ) y1 ( x, t ) y2 ( x, t )
ym sin(kx t ) ym sin( kx t )
2 ym sin(kx t 12 ) cos( 12 )
y( x, t ) 2 ym cos( 12 ) sin( kx t 12 )
The resultant sinusoidal wave – which is the result of an
interference – travels in the same direction as the two original
waves.
sin sin 2sin 12 ( ) cos 12 ( )
Erwin Sitompul University Physics: Wave and Electricity 3/10
Interference of Waves
Fully constructive Fully destructive Intermediate
interference interference interference
Erwin Sitompul University Physics: Wave and Electricity 3/11
Checkpoint
Here are four possible phase differences between two identical
waves, expressed in wavelengths: 0.2, 0.45, 0.6, and 0.8.
Rank them according to the amplitude of the resultant wave,
greatest first.
Rank: 0.2 and 0.8 tie, 0.6, 0.45
1 2 radians 360 Amplitude ym 2 ym cos( 12 )
0.2 0.4 radians 72 cos( 12 72) 0.809
0.45 0.9 radians 162 cos( 12 162) 0.156
0.6 1.2 radians 216 cos( 12 216) 0.309
0.8 1.6 radians 288 cos( 12 288) 0.809
Erwin Sitompul University Physics: Wave and Electricity 3/12
Example II
Two identical sinusoidal waves, moving in the same direction
along a stretched string, interfere with each other. The
amplitude ym of each wave is 9.8 mm, and the phase difference
Φ between them is 100°.
(a) What is the amplitude ym’ of the resultant wave due to the
interference, and what is the type of this interference?
ym 2 ym cos( 12 ) 2(9.8 mm) cos( 12 100) 12.599 mm
The interference is intermediate, which can be deducted in
two ways:
1. The phase difference is between 0 and π radians.
2. The amplitude ym’ is between 0 and 2ym.
Erwin Sitompul University Physics: Wave and Electricity 3/13
Example II
Two identical sinusoidal waves, moving in the same direction
along a stretched string, interfere with each other. The
amplitude ym of each wave is 9.8 mm, and the phase difference
Φ between them is 100°.
(b) What phase difference, in radians and wavelengths, will
give the resultant wave an amplitude of 4.9 mm?
ym 2 ym cos( 12 )
x
4.9 mm 2(9.8 mm) cos( ) 1
2
2
4.9 mm
cos( 2 )
1
2.636
2(9.8 mm) x
cos( 12 ) 0.25 2
0.420
1
2 1.3181 or 1.8235
2.6362 or 3.6470
0.420 wavelength
2.636 rad
Erwin Sitompul University Physics: Wave and Electricity 3/14
Standing Waves
The following figures shows the superposition of two waves
of the same wavelength and amplitude, traveling in opposite
direction. • Where?
There are places along the string, called nodes, where the
string never moves. Halfway between adjacent nodes, we
can see the antinodes, where the amplitude of the resultant
wave is a maximum. • Where?
The resultant wave is called standing waves because the
wave pattern do not move left or right.
Erwin Sitompul University Physics: Wave and Electricity 3/15
Standing Waves
Erwin Sitompul University Physics: Wave and Electricity 3/16
Standing Waves
To analyse a standing wave, we represent the two combining
waves with the equations:
y1 ( x, t ) ym sin(kx t )
y2 ( x, t ) ym sin(kx t )
The principle of superposition gives:
y( x, t ) y1 ( x, t ) y2 ( x, t )
ym sin(kx t ) ym sin(kx t )
y( x, t ) 2 ym sin kx cos t
sin sin 2sin 12 ( ) cos 12 ( )
Erwin Sitompul University Physics: Wave and Electricity 3/17
Standing Waves
For a standing wave, the amplitude 2ymsinkx varies with
position.
For a traveling wave, the amplitude ym is the same for all
position.
0 x
N N N N
AN AN AN
Erwin Sitompul University Physics: Wave and Electricity 3/18
Standing Waves
y( x, t ) 2 ym sin kx cos t
In the standing wave, the amplitude is zero for values of kx
that give sinkx = 0.
kx n , for n 0,1, 2,
• Nodes
xn , for n 0,1, 2,
2
In the standing wave, the amplitude is zero for values of kx
that give sinkx = ±1
kx 12 , 23 , 52 ,
kx (n 12 ) , for n 0,1, 2, • Antinodes
1
x n , for n 0,1, 2,
2 2
Erwin Sitompul University Physics: Wave and Electricity 3/19
Standing Waves and Resonance
Consider a string, such as a guitar
string, that is stretched between two
clamps.
If we send a continuous sinusoidal
wave of a certain frequency along the
string, the reflection and interference
will produce a standing wave pattern
with nodes and antinodes like those in
the figure.
Such a standing wave is said to be
produced at resonance. The string is
said to resonate at a certain resonant
frequencies.
Erwin Sitompul University Physics: Wave and Electricity 3/20
Standing Waves and Resonance
For a string stretched between
two clamps, we note that a node
must exist at each of its end,
because each end is fixed and
cannot oscillate.
The simplest patterns that meets
this requirement is a single-loop
standing wave, with two nodes
and one antinode.
A second simple pattern is the
two loop pattern. This pattern
has three nodes and two
antinodes.
A third pattern has four nodes,
three antinodes, and three loops
Erwin Sitompul University Physics: Wave and Electricity 3/21
Standing Waves and Resonance
Thus, a standing wave can be set up on a string of length L
by a wave with a wavelength equal to one of the values:
2L
, for n 1, 2,3,
n
The resonant frequencies that correspond to these
wavelengths are:
v v
f n , for n 1, 2,3,
2L
The last equation tells us that the resonant frequencies are
integer multiples of the lowest resonant frequency, f = v/2L,
for n = 1.
The oscillation mode with the lowest frequency is called the
fundamental mode or the first harmonic.
Erwin Sitompul University Physics: Wave and Electricity 3/22
Standing Waves and Resonance
The second harmonic is the oscillation mode with n = 2, the
third harmonic is that with n = 3, and so on.
The collection of all possible
oscillation modes is called
the harmonic series.
n is called the harmonic
number.
Erwin Sitompul University Physics: Wave and Electricity 3/23
Homework 3: Standing Waves
Two identical waves (except for direction of travel) oscillate
through a spring and yield a superposition according to the
equation
y (0.50 cm) sin
3
mm 1
x cos (40 min 1 )t
(a) What are the amplitude and speed of the two waves?
(b) What is the distance between nodes?
(c) What is the transverse speed of a particle of the string at
the position x = 1.5 cm when t = 9/8 s?
Erwin Sitompul University Physics: Wave and Electricity 3/24
Homework 3: Standing Waves
New
Two identical waves (except for direction of travel) oscillate
through a spring and yield a superposition according to the
equation
y (0.8 m) sin 3 cm 1 x cos ( 18 s 1 )t
(a) What are the amplitude and speed of the two waves?
(b) What is the distance between nodes?
(c) What is the transverse speed of a particle of the string at
the position x = 2.70 m when t = 0.25 min?
Erwin Sitompul University Physics: Wave and Electricity 3/25
You might also like
- 4wre 6-10 Series 1x PDFDocument12 pages4wre 6-10 Series 1x PDFArpan GajjarNo ratings yet
- Fundamentals of Energy Dispersive X-Ray Analysis: Butterworths Monographs in MaterialsFrom EverandFundamentals of Energy Dispersive X-Ray Analysis: Butterworths Monographs in MaterialsRating: 5 out of 5 stars5/5 (1)
- Electronic Devices and Circuits: In Three VolumesFrom EverandElectronic Devices and Circuits: In Three VolumesRating: 3.5 out of 5 stars3.5/5 (2)
- Electricity and Magnetism: Problems in Undergraduate PhysicsFrom EverandElectricity and Magnetism: Problems in Undergraduate PhysicsRating: 5 out of 5 stars5/5 (1)
- Fundamentals of Microwave Electronics: International Series of Monographs on Electronics and InstrumentationFrom EverandFundamentals of Microwave Electronics: International Series of Monographs on Electronics and InstrumentationNo ratings yet
- Electronic Devices and Circuits: The Commonwealth and International Library: Electrical Engineering Division, Volume 1From EverandElectronic Devices and Circuits: The Commonwealth and International Library: Electrical Engineering Division, Volume 1No ratings yet
- Feynman Lectures Simplified 2C: Electromagnetism: in Relativity & in Dense MatterFrom EverandFeynman Lectures Simplified 2C: Electromagnetism: in Relativity & in Dense MatterNo ratings yet
- Interactions between Electromagnetic Fields and Matter: Vieweg Tracts in Pure and Applied PhysicsFrom EverandInteractions between Electromagnetic Fields and Matter: Vieweg Tracts in Pure and Applied PhysicsNo ratings yet
- Advances in Structure Research by Diffraction Methods: Fortschritte der Strukturforschung mit BeugungsmethodenFrom EverandAdvances in Structure Research by Diffraction Methods: Fortschritte der Strukturforschung mit BeugungsmethodenR. BrillNo ratings yet
- O level Physics Questions And Answer Practice Papers 2From EverandO level Physics Questions And Answer Practice Papers 2Rating: 5 out of 5 stars5/5 (1)
- Introduction to Non-Linear Mechanics. (AM-11), Volume 11From EverandIntroduction to Non-Linear Mechanics. (AM-11), Volume 11No ratings yet
- Strength of Materials and Structures: An Introduction to the Mechanics of Solids and StructuresFrom EverandStrength of Materials and Structures: An Introduction to the Mechanics of Solids and StructuresRating: 4 out of 5 stars4/5 (1)
- Solid-State Circuits: Electrical Engineering DivisonFrom EverandSolid-State Circuits: Electrical Engineering DivisonRating: 4.5 out of 5 stars4.5/5 (4)
- An Introduction to the Theory of Microwave CircuitsFrom EverandAn Introduction to the Theory of Microwave CircuitsK. KurokawaNo ratings yet
- Electron Beam-Specimen Interactions and Simulation Methods in MicroscopyFrom EverandElectron Beam-Specimen Interactions and Simulation Methods in MicroscopyNo ratings yet
- Modern Electrical Installation for Craft StudentsFrom EverandModern Electrical Installation for Craft StudentsRating: 4.5 out of 5 stars4.5/5 (4)
- Unified Field Theory in a Nutshell1: The Quest for the Theory of EverythingFrom EverandUnified Field Theory in a Nutshell1: The Quest for the Theory of EverythingNo ratings yet
- Negative Mass and Negative Refractive Index in Atom Nuclei - Nuclear Wave Equation - Gravitational and Inertial Control: Part 3: Gravitational and Inertial Control, #3From EverandNegative Mass and Negative Refractive Index in Atom Nuclei - Nuclear Wave Equation - Gravitational and Inertial Control: Part 3: Gravitational and Inertial Control, #3No ratings yet
- Negative Mass and Negative Refractive Index in Atom Nuclei - Nuclear Wave Equation - Gravitational and Inertial Control: Part 4: Gravitational and Inertial Control, #4From EverandNegative Mass and Negative Refractive Index in Atom Nuclei - Nuclear Wave Equation - Gravitational and Inertial Control: Part 4: Gravitational and Inertial Control, #4No ratings yet
- The Propagation of Electromagnetic Waves in Multiconductor Transmission Lines: International Series of Monographs on Electromagnetic WavesFrom EverandThe Propagation of Electromagnetic Waves in Multiconductor Transmission Lines: International Series of Monographs on Electromagnetic WavesNo ratings yet
- Intensity of Electromagnetic Waves as a Function of Frequency, Source Distance and Aperture AngleFrom EverandIntensity of Electromagnetic Waves as a Function of Frequency, Source Distance and Aperture AngleNo ratings yet
- Maxwell's Equations and Their Consequences: Elementary Electromagnetic TheoryFrom EverandMaxwell's Equations and Their Consequences: Elementary Electromagnetic TheoryNo ratings yet
- Negative Mass and Negative Refractive Index in Atom Nuclei - Nuclear Wave Equation - Gravitational and Inertial Control: Part 2: Gravitational and Inertial Control, #2From EverandNegative Mass and Negative Refractive Index in Atom Nuclei - Nuclear Wave Equation - Gravitational and Inertial Control: Part 2: Gravitational and Inertial Control, #2No ratings yet
- Electronic Devices and Circuits: The Commonwealth and International Library: Electrical Engineering Division, Volume 3From EverandElectronic Devices and Circuits: The Commonwealth and International Library: Electrical Engineering Division, Volume 3Rating: 3 out of 5 stars3/5 (2)
- Weak Interaction of Elementary Particles: International Series of Monographs in Natural PhilosophyFrom EverandWeak Interaction of Elementary Particles: International Series of Monographs in Natural PhilosophyNo ratings yet
- LRL Accelerators, The 184-Inch SynchrocyclotronFrom EverandLRL Accelerators, The 184-Inch SynchrocyclotronNo ratings yet
- Differential Forms on Electromagnetic NetworksFrom EverandDifferential Forms on Electromagnetic NetworksRating: 4 out of 5 stars4/5 (1)
- Optical Sources, Detectors, and Systems: Fundamentals and ApplicationsFrom EverandOptical Sources, Detectors, and Systems: Fundamentals and ApplicationsNo ratings yet
- Ultrasound and Elastic Waves: Frequently Asked QuestionsFrom EverandUltrasound and Elastic Waves: Frequently Asked QuestionsNo ratings yet
- ELECTROMAGNETIC FIELDS: Exposure is not optional, no one can avoid itFrom EverandELECTROMAGNETIC FIELDS: Exposure is not optional, no one can avoid itNo ratings yet
- Fluctuations and Non-Linear Wave Interactions in Plasmas: International Series in Natural PhilosophyFrom EverandFluctuations and Non-Linear Wave Interactions in Plasmas: International Series in Natural PhilosophyNo ratings yet
- Electric Bells and All About Them A Practical Book for Practical MenFrom EverandElectric Bells and All About Them A Practical Book for Practical MenNo ratings yet
- Principles of Electric Methods in Surface and Borehole GeophysicsFrom EverandPrinciples of Electric Methods in Surface and Borehole GeophysicsRating: 3 out of 5 stars3/5 (1)
- Grease TrapDocument1 pageGrease TrapCris Angelo PangilinanNo ratings yet
- 7TCA083340R0017 pt007Document2 pages7TCA083340R0017 pt007Cris Angelo PangilinanNo ratings yet
- Field Work 3Document12 pagesField Work 3Cris Angelo PangilinanNo ratings yet
- Journal FinalDocument20 pagesJournal FinalCris Angelo PangilinanNo ratings yet
- O o o O: Project Information General InfoDocument1 pageO o o O: Project Information General InfoCris Angelo PangilinanNo ratings yet
- Field Work Peer Assessment FW 1Document2 pagesField Work Peer Assessment FW 1Cris Angelo PangilinanNo ratings yet
- ENV20 Sustainable DevelopmentDocument10 pagesENV20 Sustainable DevelopmentCris Angelo PangilinanNo ratings yet
- Exercise No. 1: Prof. Bayani F. BegasoDocument1 pageExercise No. 1: Prof. Bayani F. BegasoCris Angelo PangilinanNo ratings yet
- BusasdsadasDocument1 pageBusasdsadasCris Angelo PangilinanNo ratings yet
- Iejfaiosjdo Hnoahnasjncajscnashabscnascjklashdcnasfcoiehieruqer90qwueqw - (9fwfj'oweofjefgqe Gyegeg Svfs BFG Sbtsre Ysn Y Eruy 5n Gy RHJ Re Yu 53tgsg SF SDWQ 62 4twers GfdgdgasgdDocument1 pageIejfaiosjdo Hnoahnasjncajscnashabscnascjklashdcnasfcoiehieruqer90qwueqw - (9fwfj'oweofjefgqe Gyegeg Svfs BFG Sbtsre Ysn Y Eruy 5n Gy RHJ Re Yu 53tgsg SF SDWQ 62 4twers GfdgdgasgdCris Angelo PangilinanNo ratings yet
- Acknowledgement.... NewDocument1 pageAcknowledgement.... NewCris Angelo PangilinanNo ratings yet
- How To Pronounce German VowelsDocument2 pagesHow To Pronounce German VowelsCris Angelo PangilinanNo ratings yet
- My Seductive BossDocument203 pagesMy Seductive BossCris Angelo Pangilinan88% (8)
- Pre-Alignment Delays v.1.1 - Guide ENDocument48 pagesPre-Alignment Delays v.1.1 - Guide ENveskovac1No ratings yet
- Pinto pm5 Tif 01Document19 pagesPinto pm5 Tif 01Salem BawazirNo ratings yet
- A Practical Power System Stabilizer Tuning For GARRI Power StationDocument8 pagesA Practical Power System Stabilizer Tuning For GARRI Power StationLê Trung DũngNo ratings yet
- 3 - MEDICION DE DISTANCIAS - III - Ing JUAN VILLARREALDocument21 pages3 - MEDICION DE DISTANCIAS - III - Ing JUAN VILLARREALvictorNo ratings yet
- Expt01 ScilabDocument12 pagesExpt01 ScilabHarlz RanchNo ratings yet
- Practica 1 Osciloscopio VirtualDocument8 pagesPractica 1 Osciloscopio VirtualIsaac MartinezNo ratings yet
- Testlab Software Reference Manual - Functions and FormulasDocument12 pagesTestlab Software Reference Manual - Functions and Formulasmuhammad irfanNo ratings yet
- Signal & System - Week 1Document29 pagesSignal & System - Week 1Muhammad Feisal IliasNo ratings yet
- 3° Unidad de CuevasDocument20 pages3° Unidad de CuevasJose Antonio CruzNo ratings yet
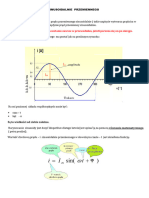
- Wielkości Prądu Sinusoidalnie PrzemiennegoDocument7 pagesWielkości Prądu Sinusoidalnie Przemiennegoasawczuk951No ratings yet
- ECEN 5737 Optional HWDocument2 pagesECEN 5737 Optional HWVIJAYPUTRANo ratings yet
- 7. Suppose an inductor has XL = 555 Ω at f = 132Document4 pages7. Suppose an inductor has XL = 555 Ω at f = 132Jhacel CelesteNo ratings yet
- PHY108L ManualDocument58 pagesPHY108L ManualSalman Hossain SahilNo ratings yet
- Getting Started Simulation Research: CASPOCDocument18 pagesGetting Started Simulation Research: CASPOCKevinNo ratings yet
- Metodos de IntegracionDocument12 pagesMetodos de Integracionnero1996No ratings yet
- In WheelMotorDesignforanElectricScooterDocument11 pagesIn WheelMotorDesignforanElectricScooterNguyen Phan LamNo ratings yet
- In Situ BalancingDocument30 pagesIn Situ Balancingzain140No ratings yet
- New Implementation of High-Precision and Instant-Response Air Thermometer by Ultrasonic SensorsDocument7 pagesNew Implementation of High-Precision and Instant-Response Air Thermometer by Ultrasonic Sensorshamza_qayyumNo ratings yet
- FASEDocument16 pagesFASEDavid MartinezNo ratings yet
- SME4 Manual ThytronicDocument22 pagesSME4 Manual ThytronicOae FlorinNo ratings yet
- Harmonic Analysis IN ANSYSDocument15 pagesHarmonic Analysis IN ANSYSSai KiranNo ratings yet
- Les Banki Circuit Updated Version August 16Document12 pagesLes Banki Circuit Updated Version August 16petar2009100% (2)
- AskDocument9 pagesAskBrenno FernandesNo ratings yet
- T5000 ManualDocument4 pagesT5000 Manualhusan shahNo ratings yet
- Vessel Theory RAOs and PhasesDocument3 pagesVessel Theory RAOs and PhasesJonathan AmaralNo ratings yet
- Digital Signal Processing FoundationsDocument29 pagesDigital Signal Processing FoundationsskanshahNo ratings yet
- CH 5 Arreglo de Fuentes PuntualesDocument31 pagesCH 5 Arreglo de Fuentes PuntualessyxtynsNo ratings yet
- Evaluación de Salida TEMA IV - Análisis de Vibraciones de Máquinas RotativasDocument19 pagesEvaluación de Salida TEMA IV - Análisis de Vibraciones de Máquinas RotativasGuido Gómez ChacónNo ratings yet
- Radio Class Test by Capt. RajDocument11 pagesRadio Class Test by Capt. RajPraveen ChoudharyNo ratings yet