Professional Documents
Culture Documents
Kinematics in One Dimension
Uploaded by
dannnnuOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Kinematics in One Dimension
Uploaded by
dannnnuCopyright:
Available Formats
Ki nemat i c s i n One
Di mensi on
P H Y S I C S
Kinematics in One Dimension
2
KINEMATICS IN ONE DIMENSION
IIT JEE Syllabus: Kinematics in one dimension (Cartesian coordinaes only), Relative velocity.
1. INTRODUCTION
Mechanics is the branch of physics that focuses on the motion of objects and the forces that cause the motion to
change. There are two branches of Mechanics: Kinematics and Dynamics. The word kinematics comes from the Greek
word "Kinema" meaning motion.
Kinematics deals with the concepts that are needed to describe motion, without any reference to forces or the
cause of the motion. The word dynamics comes from the Greek word "dynamis" meaning power.
Dynamics deals with the relation between the forces and the motion.
Scalar quantity : Any physical quantity, which can be measured on some scale, is said to be a scalar quantity. The values
of physical quantities (such as mass, distance etc.) that have only magnitude add according to the rules of arithmetic.
Mass, length, time, volume, density etc., are examples of scalar quantities.
Vector quantity : Any physical quantity, which has a magnitude as well as the direction, is called a vector quantity.
Displacement is a vector quantity. Vectors can be represented as a straight-line segment. Vectors are added by geometric
addition.
NOTE: To understand a physical quantity we should know:
Definition
Measuring Technique or Formula
Scalar or vector nature
Units
2. REVIEW OF BASIC CONCEPTS
Particle An object of negligible dimensions, i.e., a point mass is known as a particle. This is only mathematical
idealization. The earth can be treated as a particle if we consider the motion of the earth around the sun. The radius of the
earth is very small, when we compare the distance between the earth and sun.
Rest and Motion : The concept of motion is a relative one and a body that may be in motion relative to one reference
system, may be at rest relative to another.
REST :If the position of an object does not change as time passes, it is said to be at rest with reference to observer.
MOTION : If the position of the object changes as time passes, it is said to be at motion with respect to observer.
Motion is Relative : While sitting in a moving train, your distances from the walls, roof and the floor of the compartment
do not change. That is, with respect to the compartment, your position does not change. You are at rest with respect to the
compartment. But your distance from the platform, from which you boarded the train, changes as time passes. So you are
moving with respect to the platform. This means that an object can be at rest with respect to one thing and in motion with
respect to some other thing at the same time. So motion is not absolute; it is relative.
Translational Motion : The motion in which all the particles of a body move through the same distance in the same time
is called translational motion.
Examples : An automobile moving along a road, freely falling body, firing of a bullet from a gun, etc., are some of the
examples of translational motion.
The motion of translation is of two types :
1. Rectilinear Motion : When a body moves in a straight line, like a ball dropped from a height, the motion described
by the body is rectilinear motion.
Examples of rectilinear motion : A train moving along a straight track; a car moving on a straight road.
2. Curvilinear motion : When a body moves along a curved path, the motion described by the body is called curvilinear
motion.
Examples of curvilinear motion: The motion of a baseball hit in the air; a car negotiating a bend; a ball thrown
upward at an angle.
3 MEASURING POSITION :
Referense Systems and Co-ordinate System.
The motion of a particle is always described with respect to a reference system. A reference system is 'made' by
taking an arbitrary point as origin and imagining a co-ordinate system to be attached to it. This co-ordinate system chosen
for a given problem constitutes the reference system for it. We generally choose a coordinate system attached to the earth
as the reference system for most of the problems.
Kinematics in One Dimension
3
A
B
C
A
B
C
C
A
B B
A
C
Fig 1(a) Rectillinear Motion Fig 1(b) Curvillinear Motion
Fig. 1
The location of a point on a line can be described by one coordinate; a point on a plane can be described by two
coordinates; a point in a three dimensional volume can be described by three coordinates. In general, the number of
coordinates equals the number of dimensions. A coordinate system consists of :
1. a fixed reference point (origin)
2. a set of axes with specified directions and scales
3. instructions that specify how to label a point in space relative to the origin and axes.
For Example :
Cartesian coordinate system (rectangular coordinate system) : (x, y)
x0 O
y0
y
P(x0,y0)
x
Fig.2 Cartesian Co-ordinate System
Position : The position of a particle moving along a straight line is the distance of a particle specified in magnitude and
direction from the origin of a reference system.
The line shown in figure resembles with the x - axis, the position of a particle moving along a straight line is described by
x. The details of the origin, positive and negative directions are shown in Fig.3.
Negative Positive
Origin
3 2 1 0 1 2 3
Fig. 3
To describe the position of the particle at a given time, we have to specify
(i) Its distance from the origin, i.e., numberical value with unit
(ii) Whether the particle is moving towards right seen from the origin or moving towards left seen from the origin, i.e.,
the positive direction or the negative direction with the sign.
Illustration 1.
Consider the situation shown in Figure . (a) What is the position of a particle when it is at A and when it is at B? (b)
Are the two position the same? (c) Are the two distances of the particle from the origin the same ? (d) What is the position
of particle at 'O'?
Solution.
(a) The position of the particle is x =2 m when it is at A, and x =-2 m when it is at B.
(b) The two positions are not the same.
(c) The distances of the particle from the origin in the two positions are the same, and equal to 2 m.
(d) The position of the particle is x =0 m when it is at O.
4 DISTANCE TRAVELLED AND DISPLACEMENT
Trajectory : When a body is displaced from one point to another, it describes a certain curve, which is called a trajectory
of a moving body. We call the motion of a particle as rectilinear or straight line if its trajectory is a straight line.
Kinematics in One Dimension
4
The actual length covered by a moving body in between two points, irrespective of the direction in which the body is
moving, is called distance.
In the figure shown alongside, if the particle performs one complete rotation then the distance covered by it is 2t r. .
O
r
The shortest distance covered by a moving body in between two points, in a particular direction,
is called the displacement.
The 'displacement' of a particle and the 'distance travelled' by it is two different quantities. Distance travelled in a
given time has just a magnitude (numerical value) and no direction, whereas the displacement has magnitude as well as
direction. It is important to note that the magnitude of the displacement is not always the same as the distance travelled. If
a particle moves in a plane along a zig-zag path, the distance travelled in a given time interval may be much larger than the
magnitude of its displacement in the same time interval.
Displacement in straight-line motion
If a particle moves along a straight line, its displacement may be obtained by subtracting its initial position, x
1
,
from its final position, x
2
, i.e., the displacement is given by d =x
2
x
1
. It indicates both the quantities magnitude and
direction - the straight - line distance between the initial and final position as well as the direction of the final position
seen from the initial position.
Consider the following example shown in figure.
Origin
3 2 1 0 1 2 3
Fig. 4
A B
Case I Suppose that at time t
1
, the particle is at A, and at a later time t
2
, it is at B.
The position x
1
=2 m and x
2
=4 m. The displacement of the particle is
d =x
2
x
1
=4 m 2 m =2 m
Case II Suppose that at time t
1
, the particle is at B, and at a later time t
2
, it is at A.
The position is at x
1
=4 m and x
2
=2 m. The displacement of the particle is
d =x
2
x
1
=2 m 4 m =2 m
Case III Suppose that at time t
1
, the particle is at A, and at a later time t
2
, it is at A.
The position is at x
1
=2 m and x
2
=2 m. The displacement of the particle is
d =x
2
x
1
=2 m 2 m =0
From the example, we see that the displacement can be positive, negative or zero. In Fig. 4, the positive direction
is from left to the right. If the displacement of a particle is positive, its final position is to the right of the initial position.
If the displacement is negative, the final position is to the left of the initial position. If the displacement is zero, the final
position is the same as the initial position.
Thus, the sign of d gives the direction of the final position as seen from the initial position of the particle.
For motion of a particle along a straight line, a number along with a unit gives the displacement. The numerical
value of this number gives us how far the final position is from the initial position of the particle. The sign tells us the
direction.
Distance is the actual path (length) covered by a moving particle (or object) in a given interval of
time while displacement is the change in position, i.e., a vector joining initial to final position.
1. Distance is a scalar while displacement is a vector both having same SI unit m.
2. The magnitude of displacement is equal to minimum possible distance between two positions; so
Distance > |Displacement|
3. For motion between two points displacement is single-valued while distance depends on actual path
and so can have many values.
4. For a moving particle distance can never decrease with time while displacement can. Decrease in
displacement with time means body is moving towards the initial position.
IMPORTANT NOTES
Kinematics in One Dimension
5
5. For a moving particle distance can never be negative or zero while displacement can be. (Zero
displacement means that the body after motion has come back to initial position.)
Distance >0 but Displacement >=or <0
6. In general, magnitude of displacement is not equal to distance. However, it can be so if the motion is
along a straight line without change in direction.
5 UNIFORM AND NON-UNIFORM MOTION
Classification of motion
Uniform Motion If a body covers equal distances in any equal time intervals, then its motion is uniform.
Non-uniform Motion If a body covers unequal distances in any equal time intervals, then its motion is non-uniform.
Average Speed versus Instantaneous Speed Since a moving object often changes its speed during its motion, it is
common to distinguish between the average speed and the instantaneous speed. The distinction is as follows.
Instantaneous Speed - speed at any given instant in time.
Average Speed - average of all instantaneous speeds; found simply by the following formula :
Average Speed =
Total distance
Total time
Average speed in different circumstances
(a) Bodies covering different distances with different speeds :
Average speed, v
av
=
total distances covered
total time taken
=
t
d
=
...... t t t
s s s
3 2 1
3 2 1
+ +
+ +
=
|
|
.
|
\
|
+ +
+ + +
.......
v
s
v
s
...... s s s
2
2
1
1
3 2 1
Special case : If s
1
=s
2
=s ; equal distances with different speeds,
v
av
=
2 1
2 1
2 1
v v
v v 2
v
1
v
1
s
s 2
+
=
|
|
.
|
\
|
+
or
a 1 2
2 1 1
= +
[Harmonic mean]
(b) Bodies moving with different speeds in different time intervals :
t =t
1
+t
2
+t
3
+.........
Average speed =v
av
=
2 1
2 2 1 1
t t
..... t v t v
+
+ +
Special case : If t
1
=t
2
=t
3
...=t
n
=t ; equal time intervals with different speeds,
v
av
=
1 2 n 1 2
(v v ...v )t v v ....
nt n
+ + + +
=
[Arithmetic Mean]
Illustratin 2.
A car travels from city A to city B with a constant speed of 40 km/hr and returns back to city A with a constant speed
of 60 km/hr. Find its average speed during its entire journey.
Solution.
Equal distances with different speeds
1 2
av
1 2
2v v
v
v v
=
+
av
2 40 60
v
40 60
=
+
Kinematics in One Dimension
6
av
2 40 60
v
100
=
av
v 48km/ hr. =
The instantaneous speed : of an object is equal to the distance travelled by it in a short time interval .
Uniform speed : If an object travels equal distances in equal time intervals, it is said to move with uniform speed or
constant speed.
If an object moves with a uniform speed, its speed at any instant is the same as its average speed in any time
interval. If it covers a distance S in a time interval t, its speed at any instant is given by the equation.
s
v = or s =v
t
Unit of speed : The SI unit of speed is metre/second. This is written in short as m/s. If the distance is measured in
kilometers and time in hours, the speed will be in kilometer / hour, or km / h.
Velocity :
The velocity of an object is its displacement per unit time.
Velocity has magnitude as well as direction. It is a vector quantity. So velocity is "direction-aware." When evaluating
the velocity of an object, we have to keep track of direction. It would not be enough to say that an object has a velocity of
55 km/hr. For instance, we can describe an object's velocity as being 55km/hr, east.
The direction of the velocity is simply the same as the direction, which an object is moving. It would not matter
whether the object is speeding up or slowing down. If the object is moving rightwards, then its velocity is described as
being rightwards. If an object is moving downwards, then its velocity is described as being downwards.
The Velocity of an object is a quantity that gives the speed of the object as well as its direction of motion. The
velocity of an object changes if the speed or the direction of motion of an object is changed.
The unit of velocity is the same as that of speed. The SI unit of velocity is thus metre per second, written as m/s. We
often use the unit km/h for convenience.
Definition : Speed is the distance covered by a body in unit time. Velocity is the displacement of a
body in unit time.
Measuring Tecnique : Speed =Distance / Time ; Velocity =Displacement / Time
Scalar or Vector Nature : Speed is a scalar. Velocity is vector.
Units : Speed and velocity have the same units. C.G.S - cm/s M.K.S - m/s SI - m/s
Velocity of an object moving along a straight line
For an object moving along a straight line, there are only two possible directions of motion. In such a case,
magnitude of its velocity may be represented by the speed of the object. A positive sign is used before the magnitude of
velocity if it is moving in the positive direction of the motion. If an object is moving in the negative direction, its velocity
may be represented by the speed of the object and a negative sign before it. The resulting number gives the speed as well
as the direction of the motion, and hence, represents velocity.
Types of velocity
Uniform velocity :
When a body covers equal displacements in equal intervals of time in a specified direction, however short the time
intervals may be, the body is said to be moving with a uniform velcity. It means the velocity of an object does not change
as times passes. This means that the object is moving along a straight line, without changing direction, with a fixed speed.
The body will have a uniform velocity only if (i) it covers equal distances in equal intervals of time,
i.e., the magnitude does not change and (ii) its direction remains the same.
If the velocity is v, the displacement s in a time interval t is given by
s = vt
Variable velocity :
When a body covers unequal displacements in equal intervals of time in a secified direction or equal displacements
in equal intervals of time, but its direction changes, then the body is said to be moving with a variable velocity. If a car
covers 100 m in 1 minute from O to A and 200 m in 1 minute from A to B and so on, it is covering unequal distances in
equal intervals of time. Thus we can say that the car is moving with variable velocity or non-uniform velocity.
Average velocity :
The displacement of a body per unit time, when the body is actually moving with variable velocity, is called
average velocity.
Kinematics in One Dimension
7
Average velocity =
Change in Position
Total time
=
Displacement
Time
v
av
=
s
t
Instantaneous Velocity :
A velocity at one specific instant of time or at one specific point in the path. Such a velocity is called instantaneous
velocity, and it needs to be defined carefully. The instantaneous velocity at the first point can then be defined as the value
that the average velocity approaches when the second point is taken closer and closer to the first.
v =
t 0
s ds
lim
t dt
=
Regarding average speed and average velocity it is worth noting that :
1. Average speed is a scalar while average velocity is a vector both having same units (m/s).
2. Average speed or velocity depends on time interval over which it is defined.
3. For a given time interval average velocity is single valued while average speed can have many values
depending on path followed.
4. If after motion the body comes back to its initial positin,
Average velocity =0
Average speed >0 and finite
5. For a moving body average speed can never be negative or zero (unless t = ) while average velocity
can be i.e.,
Average speed >0 while
Average velocity >=or <0.
6. In general, average speed is not equal to magnitude of average velocity. However, it can be so if the
motion is along a straight line without change in direction.
Regarding speed and velocity, it is worth noting that :
1. Velocity is a vector while speed is a scalar, both having same units (m/s).
2. If during motion velocity remains constant throughout a given interval of time the motion is said
to be uniform and for uniform motion,
Instantaneous velocity =average velocity
However, converse may or may not be true, i.e., if average velocity =instantaneous velocity, the
motion may or may not be uniform.
3. If velocity is constant, speed =(|velocity|) will also be constant. However, may converse may or
may not be true, i.e., if speed =constant, velocity may or may not be constant as velocity has
direction in addition to magnitude which may or may not change, e.g., in case of straight line
motion with uniform velocity, then
|v| =constant and so speed =constant
While in case of uniform circular motion,
Speed =constant but velocity is not constant due to change in direction.
4. Velocity can be positive or negative as it is a vector but speed can never be negative.
Acceleration of an Object moving along a Straight Line :
The final mathematical quantity discussed is acceleration. An often-confused quantity is acceleration. Acceleration
has to do with changing how fast an object is moving. If an object is not changing its velocity, then the object is not
accelerating. Anytime an object's velocity is changing, that object is said to be accelerating; it has acceleration.
Acceleration is defined as the change in velocity per unit time. It is a vector quantity. It is represented by the
symbol 'a'. Mathematically
v- u
a=
t
Where a =acceleration, u =initial velocity
v =final velocity, t =time
Kinematics in One Dimension
8
The SI unit of acceleration is m/s
2
. If the acceleration of a body is 'a' m/s
2
, it means the velocity of the body is
increasing by 'a' units for every second.
Types of Acceleration :
Uniform Acceleration or constant acceleration : If the velocity of the body changes equal amounts in equal intervals of
time, then it is said to be in uniform acceleration. This is reffered to as a constant acceleration since the velocity is
changing by a constant amount each second. An object with a constant acceleration should not be confused with an object
with a constant velocity. If an object is changing its velocity - whether by a constant amount or a varying amount - then it
is an accelerating object. And an object with a constant velocity is not accelerating.
If the velocity of a uniformly accelerating body changes from u to v, then its acceleration is given by
a =
t
u v
Rearranging the above formula, we will get the following equation :
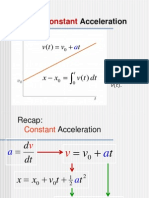
v = u + at
The Direction of the Acceleration Vector
Since acceleration is a vector quantity, it will always have a direction associated with it. The direction of the
acceleration vector depends on two things :
Whether the object is speeding up or slowing down
Whether the obect is moving in the +ve or ve direction.
The general Rule of thumb is :
If an object is slowing down, then its acceleraton is in the opposite direction of its motion.
Deceleration : If the speed of a particle decreases wth time, we say that it is decelerating, or it has deceleration or
retardation. The acceleration of the body is opposite to that of velocity, and then the body decelerates.
Non-uniform acceleration :
If the velocity of the body changes unequal amounts in equal intervals of time, then it is said to be in non-uniform
acceleration.
Average acceleration :
The average acceleration of any object over a given interval of time can be calculated using the equation
a =
t
v
A
A
=
change in velocity
time interval
Illustration 3.
A bird flies north at 20 m/s for 15 s. It rests for 5 s and then flies south at 25 m/s for 10 s. For the whole trip find,
(a) the average speed (b) the average velocity (c) the average acceleration
Solution.
Distance travelled towards north =AC =20 m/s
15 s =300 m.
Distance travelled towards south =CB =25 m/s 10 s =250 m.
B
A
path
C
Average Speed =
time
distance
=
10 5 15
250 300
+ +
+
m/s =18.34 m/s.
Average velocity =
time
et displacemn
=
10 5 15
250 300
+ +
=1.67 m/s
Kinematics in One Dimension
9
Average Acceleration, a
av
=
t
v v
t
v
i f
A
=
A
A
=
(-25) - (+20)
30
m/s
2
= 1.5 m/s
2
.
Instantaneous acceleration : Instantaneous acceleration is given by the following formula :
a =
t
v
t A
A
A
Lt
0
=
v d
dt
Regarding the acceleration it is worth noting that
1. It is a vector with SI units (m/s
2
)
2. If acceleration is zero, velocity will be constant and the motion will be uniform. However, if acceleration
is constant, acceleration is uniform but motion is non-uniform and if acceleration is not constant both
motion and acceleration are non-uniform.
3. Acceleration can be positive or negative.
6. EQUATIONS OF KINEMATICS AND PROBLEM-SOLVING :
The Equations of Kinematics
s = ut +
2
1
at
2
v
2
- u
2
= 2as
v = u + at
s =
2
v u+
t
There are a variety of symbols used in the above equations. Each symbol has its own specific meaning.
The symbol S stands for the displacement of the object
The symbol t stands for the time for which the object moved.
The symbol 'a' stands for the acceleration of the object.
And the symbol u stands for the initial velocity value of the object.
The symbol v stands for final velocity value of the object.
Each of these four equations appropriately describes the mathematical relationship between the parameters of an
object's motion. As such, they can be used to determine unknown information about an object's motion if other information
is known.
Illustration 4.
Derive a formula for finding the displacement of a body in the n
th
second.
Solution.
Let the displacement of a body in n
th
second be S
n
.
The displacement for n seconds =S
1
.
The displacement for (n-1) seconds =S
2
.
For an initial velocity u and constant acceleration a, the formula for finding the displacement is
S = ut +
2
1
at
2
S
1
=un +
2
1
an
2
S
2
=u(n-1) +
2
1
a (n-1)
2
But S
1
S
2
=displacement of body in the n
th
second i.e., S
n
.
S
n
= S
1
S
2
= un +
2
1
an
2
[u(n-1) +
2
1
a (n-1)
2
]
Kinematics in One Dimension
10
S
n
= un + 0.5an
2
[un u + 0.5a (n
2
+12n)]
S
n
=un +0.5an
2
un +u 0.5 an
2
0.5a +an
S
n
=u - 0.5a +an =u +a (n 0.5)
S
n
=u +a (n
2
1
)
Therefore the displacement of the body in the n
th
second is,
S
n
=u +a (n
2
1
)
Special Cases of Equations of Kinematics
1. If a body starts from rest, then the initial velocity, u = 0 and the equations of kinematics are :
v =at ; S =
2
1
at
2
; v
2
=2aS
2. If a body comes to rest, then v =0 and acceleration becomes negative. Then the equations of kinematics are :
u at = 0 ; S = ut
2
1
at
2
; u
2
= 2aS
3. If a body has uniform velocity then change in velocity is zero, i.e., a =0, and the equation of kinematics are :
v =u ; S =ut
Illustration 5.
A particle starting from rest, covers a distance s, moving along a straight line and comes to rest. It has a uniform
aceleration and retardation, in its two parts of journey. If v be the maximum velocity attained by it, show that the
total time of motion is 2s/v.
v
S1 S2
A B t1 t2
Solution.
Let s
1
and s
2
be the displacement of the particle in the first and second parts of the journey respectively, so that s
1
+s
2
=s (figure.)
If t
1
and t
2
be the corresponding times, then
Using s =
u+
t
2
| |
|
\ .
We have s
1
=
1
(0+v)t
2
and s
2
=
2
( + 0)t
2
Adding, we get (s
1
+s
2
) =
2
(t
1
+t
2
)
i.e., t
1
+t
2
=
2s
....... [
s
1
+s
2
=s]
Total time =
2s
Illustration 6.
A train stopping at two stations d distance apart takes t time on the journey from one station to the other. Assuming
that its motion is first that of uniform acceleration o and then that of uniform retardation | , show that
2
1 1 t
2d
+ =
o |
Solution.
Let A and B be the stations d distance apart. Further let the train accelerate from A to C, over a distance s
1
and then
decelerate from C to B, over a distance s
2
. Also, let v be the maximum velocity attained. If t
1
be the time from A to
Kinematics in One Dimension
11
C, then
s
1
=
1 1
0+v v
t = t
2 2
| |
|
\ .
u v
using s
2
( + | |
=
| (
\ .
t
.............. (1)
and t
2
be the time from C to B, then s
2
= 2
t
2
0
|
.
|
\
| + v
s
2
=
2
v
t
2
............... (2)
Adding equaitons (1) and (2), we get
s
1
+s
2
=
2
v
(t
1
+t
2
)
d =
2
v
(t) ..............(3)
Again for the motion from A to C, v = o t
1
..............(4) [ u 0] =
and for motion from C to B, | =b t
2
................(5) [ u 0] =
From equaitons (4) and (5), v (
|
+
o
1 1
=t
1
+t
2
=t
Hence, from equation (3), v =
t
d 2
2d 1 1
+ =t
t
| |
| |
| |
\ .
\ .
2
1 1 t
2d
+ =
o |
7. EQUATIONS OF KINEMATICS AND FREE FALL
The conceptual characteristics of freely falling object are described as follows : An object in free fall experiences
an acceleration of -9.8 m/s
2
. (The sign indicates a downward acceleration.) Whether explicitly stated or not, the value
of the acceleration in the kinematics equations is 9.8 m/s
2
for any freely falling object.
If an object is merely dropped (as opposed to being thrown) from an elevated height to the ground below, then the
initial velocity of the object is 0 m/s.
If an object is projected upwards in a perfectly vertical direction, then it will slow down as it rises upward. The
instant at which it reaches the peak of its trajectory, its velocity is 0 m/s. This value can be used as one of the motion
parameters in the kinematics equations; for example, the final velocity (v) after travelling to the peak would be
assigned a value of 0 m/s.
If an object is projected upwards in a perfectly vertical direction, then the velocity at which it is projected is equal
in magnitude and opposite in sign to the velocity, which it has when it returns to the same height. That is, a ball
projected vertically with an upward velocity of +30 m/s will have a downward velocity of 30 m/s when it returns
to the same height.
We can use equations of motion for freely falling bodies. If a body is falling from a height 'h' with an acceleration
due to gravity 'g' then the equations of motion becomes :
v =u +gt
h =ut +
2
1
gt
2
v
2
u
2
=2gh
If the initial velocity of freely falling bodies is zero i.e. u =0
Then, the equations of motion become :
v =gt
Kinematics in One Dimension
12
h =
2
1
gt
2
v
2
=2gh
If a body is projected vertically upwards, then what are the equations of motion? We are considering the acceleration
due to gravity of a freely falling body as positive, we take a negative value for a body projected upwards, and the
equations of motion are
v =u gt
h =ut
2
1
gt
2
v
2
u
2
=2gh
When a body is projected upwards with a velocity 'u', it is raised to a certain height and then it starts falling down.
Time of flight :
2
1
s ut gt
2
= +
| | s 0 =
t =T
2u
T
g
=
Time of descent =time of ascent =
u
g
.
8. MOTION ON AN INCLINED PLANE :
(i) Suppose a body of mass m is allowed to move down the plane with an initial velocity zero. i.e., from the position
of rest. Let the plane is inclined at an angle
u
w.r.t. horizontal direction and the body is at a height h at initial
instant (t =0) (Fig)
u
mg cosu
mg
mg sinu
u
s
R
h
fig 9
Hence in such a case, u =0, a =g sin
u
=constant and equations of motion are :
v =(g sin
u
)t
s =
2
1
(gsin
u
)t
2
and v
2
=2 (g sin
u
)s
where s is the distance travelled by the body along the plane in time t, when it reaches at the bottom.
(ii) If s is given, then : t
2
=
u sin g
s 2
or t
2
s.
If t' is the time taken to travel
4
1
th of the total distance, then : t'
2
4
s
Hence,
2
t' 1
t 4
| |
=
|
\ .
or t' =
2
t
Kinematics in One Dimension
13
i.e., in first halftime the body moves
4
1
th of the total distance while in next half it moves
4
3
th of the total distance
on an inclined plane.
(iii) Time taken to move down an inclined plane
s =
2
1
(g sin
u
) t
2
or t = ) sin g / s 2 ( u
As
s
h
=sin
u
or s =
u sin
h
, Hence t =
1 2h
sin g
(iv) Because, v
2
=2g sin
u
. s and s =
u sin
h
Hence v
2
=2g sin
u
u sin
h
=2 gh or v = ] gh 2 [
Thus, speed is independent of
u
and depend on height h.
NOTE :
(i) If two bodies allowed to move down from same height along two inclined planes having different gradients
u
1
and
u
2
(
u
1
>
u
2
) (Fig.) then final velocity acquired by both will be same i.e., v
1
=v
2
= ] gh 2 [
h
u1 u2
Fig.10
(ii)
1 2h 1
t t
sin g sin
=
u u
Because
u
1
>
u
2
, hence t
1
<t
2
(v) If we compare the behaviour of two identical bodies moving under gravity in different conditions i.e., one falling
vertically downwards and other moving along an inclined plane from same height h, then in case of first body :
v
F
= ] gh 2 [ , a
F
=g and t
F
=
g
h 2
but in the case of second body,
v
s
= ] gh 2 [ , a
s
=g sin
u
and t
s
=
g
h 2
sin
1
u
Hence, v
F
=v
s
, a
F
>a
s
and t
F
<t
s
.
Illustration 7.
A body starting from rest slide on an inclined plane of length s as shown in fig. the time taken to cover half the
distance.
Sol. When a body slides on an inclined plane, acceleration of the body a =g sin
u
=constant. So, equation of motion
can be applied. From equaiton of motion, here
s =0 +1/2 (g sin
u
) t
2
[as u =0] ........... (1)
Kinematics in One Dimension
14
h
S
R
mg
u
mg cosu
If s' =
2
s
,
2
t
' t
s
) 2 / s (
|
.
|
\
|
=
i.e., t' =
2
t
~
0.7 t
i.e., in about 0.7 times the time of descent the body covers half of the total distance.
Illustration 8.
A mass A is released from the top of a frictionless inclined plane 18 m long and reached the bottom 3 s. later. At the
instant when A is released, a second mass B is projected upwards along the plane from the bottom with a certain
initial velocity. The mass B travels a distance up the plane, stops and returns to the bottom so that it arrives
simultaneously with A. The two masses do not collide. Find the acceleration and initial velocity of B. How far up
the inclined plane does B travel?
Sol. Acceleration down the plane, a =g sin
u
=constant for two masses. A starts from rest, 18 =0
3 +
2
1
a
3
2
.
i.e., a =4 m/s
2
. ................. (1)
Now if B is projected up the plane with a velocity u, it will go up the plane till its velocity becomes zero i.e., (v =
0) as for it acceleration will be down the plane. So from equation of motion, time taken to go up the plane.
18m
C
v=0
u=0
B
0 =u at
1
i.e., t
1
=(u / a) ............ (2)
and from equation of motion distance moved up the plane
0 =u
2
2as, i.e., s =(u
2
/ 2a) ..............(3)
Now the body B will slide down the plane and so time taken by it to slide a distance s down the plane starting from
rest at C, from equation of motion, s =0 +
1
/
2
at
2
2
.
i.e., t
2
=
2 2
2 u u u
s
a 2a a 2a
| | | |
= = | |
| |
\ . \ .
..............(4)
But it is given that body B reaches to ground with A,
i.e., t
1
+t
2
=3 or
a
u 2
=3 [as from Eqns. (2) and (4), t
1
=t
2
=u/a]
or u =
2
3
a =
2
3
4 =6 m / s. [as from Eqns. (1) a =4]
So the acceleration of B is 4 m/s
2
down the plane while its velocity is 6 m/s up the plane.
(The distance travelled by B up the plane from Eqns. (3) i.e., s =(u
2
/ 2a) =4.5 m)
Illustration 9.
A body is projected from the bottom of a smooth inclined plane with a velocity of 10 m/s. If it be just sufficient to
carry it to the top in 2s, find the inclination and height of the plane. [g =10 m/s
2
]
Sol. Let AB be the inclined plane, with angle of inclination o and height h. (figure)
Kinematics in One Dimension
15
Now, for the motion along the plane up,
o
C
A
h
u=10 m/s
t=25 B
u =10; a =10 sin o ; v =0; t =2s
Using v =u +at
we have 0 =10 (10 sino ) (2) sin o =
10
20
o =30
o
Now, using u
2
=2gh,
we have h =
2
10
2 10
=5 m
Illustration 10.
A particle starts from rest from the top of a smooth inclined plane of a given base. Find the inclination of the plane
to the horizontal, for the time of fall to be least.
Sol. Let 'x' be the base of the inclined plane and '
u
' any angle of inclination;
Length of the incline AB =x sec
u
. (figure)
S
u
x
C
A
B
Now, for the motion along BA,
s =x sec
u
; a =g sin
u
; u =0; t =?
Using, s =ut +
2
1
at
2
; x sec
u
=
2
1
g sin
u
t
2
t =
2x
sin cos u u g
=
4x
sin 2u g
(
2 sin
u
cos
u
=sin 2
u
)
For minimum time of fall, sin 2 should be maximum, i.e., sin 2 1 u =
0
2 90 u =
;
0
45 u =
Kinematics in One Dimension
16
PROBLEM - SOLVING TECHNIQUE
Motion of a particlein a straight line
To determine the motion of a particle on an axis :
1. Select the origin of the x axis and the direction in which the axis is positive. Usually, it is best to place
the particle at the origin at time t =0; then, x
0
=0. A sketch showing the axis is helpful. It is also helpful
to show the position of the particle at some later time on the same sketch.
2. Take the positive direction of the velocity and the acceleration in the same direction as the axis.
3. State the problem in your own words and then translate into symbols and equations. For example, the
problem might ask "When does the particle arrive at x =10m?" You might paraphrase this is as "What
is the value of time t when x =10m?" Or, the problem may read "Where is the particle when its velocity
is v =10m/s?" which you then paraphrase as "What is the value of x when v =10m/s?".
4. Make a list of given quantities, such as the initial position x
0
, the initial velocity v
0
, and the initial
acceleration a
0
.
5. Identify the unknowns, and label them with symbols. Use kinematic Eqs. to relate the unknowns to the
knowns. Solve for the unknowns in terms of the known values. Sometimes you will have to solve
simultaneous equations for the unknowns.
6. Examine your results carefully to see whether they make sense.
You might also like
- MomentumDocument93 pagesMomentumSteve100% (1)
- Mechanics L7Document49 pagesMechanics L7Charlie LaiNo ratings yet
- Tipler&Mosca Ch08 Conservation of Linear MomentumDocument116 pagesTipler&Mosca Ch08 Conservation of Linear MomentumIanNo ratings yet
- Mechanics: Kinematics and DynamicsDocument4 pagesMechanics: Kinematics and DynamicsSaifur RahmanNo ratings yet
- Part 04 SET (251 - 252)Document3 pagesPart 04 SET (251 - 252)KartikNo ratings yet
- 01b - Vector and ScalarDocument7 pages01b - Vector and Scalarruth ranselNo ratings yet
- 1.1 - 1.3introduction To Physics & The QuantityDocument7 pages1.1 - 1.3introduction To Physics & The QuantityayepingpongNo ratings yet
- Wk2d2. Motion in One Dimension 1dDocument32 pagesWk2d2. Motion in One Dimension 1dAlex DeveldosNo ratings yet
- Uniform and Non - Uniform Circular MotionDocument4 pagesUniform and Non - Uniform Circular MotionExpertsmindEduNo ratings yet
- Dynamics (Work and Energy) TutorialDocument5 pagesDynamics (Work and Energy) TutorialYadana1No ratings yet
- Worksheet Uniform Circular MotionDocument1 pageWorksheet Uniform Circular Motionbangtanswifue -No ratings yet
- Motion in One DimensionDocument13 pagesMotion in One DimensionMohammed Aftab Ahmed100% (1)
- Dependent Motions - : Dynamics of Rigid BodiesDocument22 pagesDependent Motions - : Dynamics of Rigid BodiesCllyan ReyesNo ratings yet
- C3 Kinematics 1dimDocument18 pagesC3 Kinematics 1dimdavincoNo ratings yet
- Motion in Two or Three DimensionsDocument58 pagesMotion in Two or Three DimensionsMarc Howard Detera PanganibanNo ratings yet
- Honors Physics Midterm Review: Exam DayDocument8 pagesHonors Physics Midterm Review: Exam DayEarl averzosaNo ratings yet
- Physics 71 1st Long ExamDocument12 pagesPhysics 71 1st Long ExamAb YZNo ratings yet
- Free FallDocument7 pagesFree FallFatin Naqiya Roslan50% (2)
- Work Sheet 3 ADocument9 pagesWork Sheet 3 Adaniel hambissaNo ratings yet
- Module #1 - Simple Stress: Engr. Lito I. MauroDocument38 pagesModule #1 - Simple Stress: Engr. Lito I. MauroJeffrey ManansalaNo ratings yet
- Relative Motion of ProjectilesDocument13 pagesRelative Motion of Projectilesumapavani0% (1)
- Mathematical Modeling of Control System Assignment NewDocument8 pagesMathematical Modeling of Control System Assignment NewJawad SandhuNo ratings yet
- Projectile Motion Experiment ReportDocument5 pagesProjectile Motion Experiment ReportDương Quang MinhNo ratings yet
- Chapter 1Document20 pagesChapter 1KennethTrucillaCortezNo ratings yet
- 252Document15 pages252Ankush SharmaNo ratings yet
- Chap4 000Document5 pagesChap4 000pja752No ratings yet
- Chapter10 PDFDocument39 pagesChapter10 PDFAyush AryanNo ratings yet
- Displacement and Velocity Worksheet1Document3 pagesDisplacement and Velocity Worksheet1api-238041530No ratings yet
- Motion in One Dimension: Pre-AP PhysicsDocument45 pagesMotion in One Dimension: Pre-AP PhysicsJohn HobanNo ratings yet
- Conceptual QuestionsDocument4 pagesConceptual QuestionssmrutirekhaNo ratings yet
- Enggphys Modules - Student Copy - ST 2022Document177 pagesEnggphys Modules - Student Copy - ST 2022Kyla Jynell SaquitonNo ratings yet
- Kinematics WorksheetDocument3 pagesKinematics WorksheetDyanie PlummerNo ratings yet
- PROBLEM - SOLVING - Friction and 2nd Law UstDocument34 pagesPROBLEM - SOLVING - Friction and 2nd Law UstMarj Ladica MangaNo ratings yet
- Projectile Motion Lab Syeed HasanDocument8 pagesProjectile Motion Lab Syeed Hasanapi-130453141No ratings yet
- Test Bank For Introduction To Physical Science 14th Edition Shipman Wilson Higgins TorresDocument17 pagesTest Bank For Introduction To Physical Science 14th Edition Shipman Wilson Higgins TorresaimeeNo ratings yet
- Kinematics Test W SolutionsDocument5 pagesKinematics Test W SolutionsNicholas ChevalierNo ratings yet
- Problem - 3A PDFDocument14 pagesProblem - 3A PDFMonicaNo ratings yet
- 1-15-15 Kinematics AP1 - Review SetDocument8 pages1-15-15 Kinematics AP1 - Review SetLudwig Van Beethoven100% (1)
- CH 04Document46 pagesCH 04AlonsoNo ratings yet
- Uniform Circular MotionDocument46 pagesUniform Circular MotionAllen EspinosaNo ratings yet
- DPP - Impulse & MomentumDocument6 pagesDPP - Impulse & MomentumMohammed Aftab AhmedNo ratings yet
- Physics 11Document11 pagesPhysics 11moorchehNo ratings yet
- Newton 2nd LW PDFDocument7 pagesNewton 2nd LW PDFMaRk KenchiNo ratings yet
- Chapter 5 Energy WorkDocument103 pagesChapter 5 Energy WorkunoNo ratings yet
- Physics Final ExamDocument3 pagesPhysics Final ExamJoey Aguilar VelascoNo ratings yet
- MHS Physics Problems Chapter 1Document27 pagesMHS Physics Problems Chapter 1Dina Ashraf0% (1)
- ExAm-Applying Newton's LawsDocument21 pagesExAm-Applying Newton's LawsOnur YavuzcetinNo ratings yet
- Circular Motion ReviewDocument10 pagesCircular Motion ReviewKimberley OrozcoNo ratings yet
- Basic Modes of Heat TransferDocument15 pagesBasic Modes of Heat Transfermeraj100% (1)
- Test - Unit 3 - Energy and MomentumDocument4 pagesTest - Unit 3 - Energy and Momentumascd_msvuNo ratings yet
- Physics - Module 1 - Moving AboutDocument19 pagesPhysics - Module 1 - Moving AboutGeoffNo ratings yet
- Projectile Motion Lab ReportDocument6 pagesProjectile Motion Lab Reportapi-439198935No ratings yet
- Experiment 3: Kinematics of Translation Laboratory ReportDocument5 pagesExperiment 3: Kinematics of Translation Laboratory ReportMan DejeloNo ratings yet
- Projectile MotionDocument21 pagesProjectile Motionapi-267685991No ratings yet
- 12 - SPH0301MMM - Projectile Motion Lab Report KEYDocument2 pages12 - SPH0301MMM - Projectile Motion Lab Report KEYChirag HablaniNo ratings yet
- 33 Engineering PhysicsDocument101 pages33 Engineering Physicskenneth roblesNo ratings yet
- G12 Constrained Motion of Connected ParticlesDocument14 pagesG12 Constrained Motion of Connected Particlesrahulnag10febNo ratings yet
- Class IX SCIENCE IITFoundation & Olympiad Study Package (PDFDrive)Document234 pagesClass IX SCIENCE IITFoundation & Olympiad Study Package (PDFDrive)Tawheed AlamNo ratings yet
- KinematicsDocument58 pagesKinematicsdevendraNo ratings yet
- KinamaticsDocument10 pagesKinamaticsChathur ChandrasooryaNo ratings yet
- Mathematics Paper For Class-X 2010Document8 pagesMathematics Paper For Class-X 2010Apex Institute100% (2)
- Momentum Assignment Class 9Document4 pagesMomentum Assignment Class 9Apex Institute0% (1)
- Organic Chemistry DPPDocument41 pagesOrganic Chemistry DPPApex Institute100% (4)
- Instructions: Duration Is 2 Hours)Document16 pagesInstructions: Duration Is 2 Hours)Apex InstituteNo ratings yet
- Class-Ix Sunday TestDocument2 pagesClass-Ix Sunday TestApex Institute100% (2)
- Jee-Mains Test Paper - 04Document20 pagesJee-Mains Test Paper - 04Apex InstituteNo ratings yet
- Class - X Sample Paper PDFDocument16 pagesClass - X Sample Paper PDFApex Institute0% (1)
- Instructions: Duration Is 2 Hours)Document16 pagesInstructions: Duration Is 2 Hours)Apex Institute100% (1)
- Instructions: Duration Is 2 Hours)Document16 pagesInstructions: Duration Is 2 Hours)Apex Institute100% (1)
- Class - X Sample Paper PDFDocument16 pagesClass - X Sample Paper PDFApex Institute0% (1)
- Maths Class X Sample Paper 03 For Board Exam 2019 PDFDocument4 pagesMaths Class X Sample Paper 03 For Board Exam 2019 PDFApex Institute100% (1)
- Class X Sample Paper 03 For Board Exam 2019 PDFDocument4 pagesClass X Sample Paper 03 For Board Exam 2019 PDFApex Institute100% (1)
- Jee-Mains Test Paper - 02Document21 pagesJee-Mains Test Paper - 02Apex InstituteNo ratings yet
- Jee-Mains Test Paper - 03Document21 pagesJee-Mains Test Paper - 03Apex Institute100% (1)
- Class X Sample Paper 01 For Board Exam 2019 PDFDocument4 pagesClass X Sample Paper 01 For Board Exam 2019 PDFApex InstituteNo ratings yet
- Plant Kingdom, Animal Kingdom, Evolution TestDocument5 pagesPlant Kingdom, Animal Kingdom, Evolution TestApex InstituteNo ratings yet
- Organic Chemistry Basic Principles NEET PaperDocument5 pagesOrganic Chemistry Basic Principles NEET PaperApex InstituteNo ratings yet
- Class XII Physics Board Paper 2018Document3 pagesClass XII Physics Board Paper 2018Apex Institute100% (1)
- NTSE Stage - 1 Mock Test - 1Document14 pagesNTSE Stage - 1 Mock Test - 1Apex InstituteNo ratings yet
- Maths Class X Sample Paper 02 For Board Exam 2019 PDFDocument4 pagesMaths Class X Sample Paper 02 For Board Exam 2019 PDFApex InstituteNo ratings yet
- Section - A: Sample Test - 2Document4 pagesSection - A: Sample Test - 2Apex Institute0% (1)
- NTSE Stage - 1 Mock Test - 2Document16 pagesNTSE Stage - 1 Mock Test - 2Apex InstituteNo ratings yet
- Mathematics Chapterwise Assignment For Class 10 Summative Assessment-1Document13 pagesMathematics Chapterwise Assignment For Class 10 Summative Assessment-1Apex Institute100% (2)
- NTSE Stage - 1 Mock Test - 3Document16 pagesNTSE Stage - 1 Mock Test - 3Apex Institute100% (1)
- Summative Assessment-1 Class 9 Mathematics Guess Paper 2016Document4 pagesSummative Assessment-1 Class 9 Mathematics Guess Paper 2016Apex Institute0% (1)
- Class-X Mathematics H.O.T.S. Summative Assessment-II 2016-17Document2 pagesClass-X Mathematics H.O.T.S. Summative Assessment-II 2016-17Apex Institute50% (2)
- Part Test For Aipmt 2016Document18 pagesPart Test For Aipmt 2016Apex InstituteNo ratings yet
- Class-IX Mathematics H.O.T.S. Summative Assessment-II 2016-17Document2 pagesClass-IX Mathematics H.O.T.S. Summative Assessment-II 2016-17Apex Institute0% (1)
- Mathematics Chapter-Wise Assignment For Class 9 Summative Assessment-1Document30 pagesMathematics Chapter-Wise Assignment For Class 9 Summative Assessment-1Apex Institute86% (7)
- Part Test For IIT Mains 2016Document21 pagesPart Test For IIT Mains 2016Apex Institute100% (1)
- KrauseproblemsDocument3 pagesKrauseproblemsapi-255059274No ratings yet
- Calculation of The Equivalent Resistance and Impedance of The Cylindrical Network Based On Recursion-Transform MethodDocument12 pagesCalculation of The Equivalent Resistance and Impedance of The Cylindrical Network Based On Recursion-Transform Methodmark_990566444No ratings yet
- Notation For Differentiation - WikipediaDocument11 pagesNotation For Differentiation - WikipediaTibor VéghNo ratings yet
- Chapter 2 Practice AnswersDocument4 pagesChapter 2 Practice AnswersZeyad Moustafa100% (1)
- Human Errors Analysis and Safety Management SystemsDocument48 pagesHuman Errors Analysis and Safety Management SystemsBambang ApriyantoNo ratings yet
- OCR Core 1 Jan 05Document4 pagesOCR Core 1 Jan 05Shamil Nunhuck100% (1)
- Assignment 1 ELL701Document21 pagesAssignment 1 ELL701Bet3aNo ratings yet
- Curve and SurfacesDocument28 pagesCurve and SurfacesAnonymous u87aqFoNo ratings yet
- Faulhaber's Formula The Sum of The R-TH Powers of The First N Positive Integers Is Given byDocument1 pageFaulhaber's Formula The Sum of The R-TH Powers of The First N Positive Integers Is Given byVice SonNo ratings yet
- امتحان على اول 3 وحدات للصف الأول الإعدادى الترم الاول 2022 مستر محمد عمارة موقع دروس تعليمية اون لاينDocument2 pagesامتحان على اول 3 وحدات للصف الأول الإعدادى الترم الاول 2022 مستر محمد عمارة موقع دروس تعليمية اون لاينBasel ElfalahaNo ratings yet
- Aminpro Addin Guide 1.2-1Document16 pagesAminpro Addin Guide 1.2-1John Calero OrtegaNo ratings yet
- ExercisesDocument8 pagesExercisesKayalvizhi Selvam0% (1)
- Piping & Instrumentation DiagramsDocument19 pagesPiping & Instrumentation Diagramsian ridz100% (1)
- Unpaired Image-To-Image Translation Via Schrondinger BridgeDocument15 pagesUnpaired Image-To-Image Translation Via Schrondinger BridgePixel DinosaurNo ratings yet
- Hybrid Artificial Neural Network and Genetic Algorithm Model For Multi-Objective Strength Optimization of Concrete With Surkhi and Buntal FiberDocument5 pagesHybrid Artificial Neural Network and Genetic Algorithm Model For Multi-Objective Strength Optimization of Concrete With Surkhi and Buntal FiberItx hamzaNo ratings yet
- Wednesday, June 9, 2021 8:08 PM: Module 2 Page 1Document19 pagesWednesday, June 9, 2021 8:08 PM: Module 2 Page 1Jaye Allen Catacutan0% (1)
- Kcse 2019 Prediction-All PDFDocument220 pagesKcse 2019 Prediction-All PDFBadmind JnrNo ratings yet
- Syllabus of Advanced Excel, Dash Board and Vba2Document6 pagesSyllabus of Advanced Excel, Dash Board and Vba2Purnangshu RoyNo ratings yet
- Modeling and Simulation of A Spray Column For NOx AbsorptionDocument15 pagesModeling and Simulation of A Spray Column For NOx AbsorptionAnel MamaniNo ratings yet
- MCQ'S Engineering Mathematics-II: Differential EquationDocument21 pagesMCQ'S Engineering Mathematics-II: Differential EquationDurga JoshiNo ratings yet
- Data Science Is New-Age Astrology: Astrology and Machine LearningDocument6 pagesData Science Is New-Age Astrology: Astrology and Machine LearningRtdfAbNo ratings yet
- Geophysical Signal AnalysisDocument481 pagesGeophysical Signal AnalysisDimas Pradana100% (1)
- Numericals SolutionDocument6 pagesNumericals SolutionMenaka SrinivasanNo ratings yet
- 2022-3-Midterm Exam in Educ 602-Part 2Document6 pages2022-3-Midterm Exam in Educ 602-Part 2Sharlene Mae DeiparineNo ratings yet
- Lec06 - Ordinary Differential Equations (BVP) - Shooting MethodsDocument39 pagesLec06 - Ordinary Differential Equations (BVP) - Shooting MethodsALYAMITHA NADIYAH SYAFITRI BAUDNo ratings yet
- Km31401 Makmal IV AcDocument3 pagesKm31401 Makmal IV AcChee OnnNo ratings yet
- Buckling Column Assignmnet 2 ECS226&ECS238Document6 pagesBuckling Column Assignmnet 2 ECS226&ECS238udinhensembabiNo ratings yet
- Hashtable #Include #Include #Include #IncludeDocument4 pagesHashtable #Include #Include #Include #IncludePaulina VoicuNo ratings yet
- Kindergarten Math TestDocument7 pagesKindergarten Math Testjonalyn brusolaNo ratings yet
- Follow your interests: This will make you feel better about yourself and what you can do.: inspiration and wisdom for achieving a fulfilling life.From EverandFollow your interests: This will make you feel better about yourself and what you can do.: inspiration and wisdom for achieving a fulfilling life.No ratings yet
- Dumbing Us Down: The Hidden Curriculum of Compulsory SchoolingFrom EverandDumbing Us Down: The Hidden Curriculum of Compulsory SchoolingRating: 4.5 out of 5 stars4.5/5 (498)
- Summary: The Laws of Human Nature: by Robert Greene: Key Takeaways, Summary & AnalysisFrom EverandSummary: The Laws of Human Nature: by Robert Greene: Key Takeaways, Summary & AnalysisRating: 4.5 out of 5 stars4.5/5 (30)
- Stoicism The Art of Happiness: How the Stoic Philosophy Works, Living a Good Life, Finding Calm and Managing Your Emotions in a Turbulent World. New VersionFrom EverandStoicism The Art of Happiness: How the Stoic Philosophy Works, Living a Good Life, Finding Calm and Managing Your Emotions in a Turbulent World. New VersionRating: 5 out of 5 stars5/5 (51)
- How to Talk to Anyone: Learn the Secrets of Good Communication and the Little Tricks for Big Success in RelationshipFrom EverandHow to Talk to Anyone: Learn the Secrets of Good Communication and the Little Tricks for Big Success in RelationshipRating: 4.5 out of 5 stars4.5/5 (1135)
- Summary: It Didn't Start with You: How Inherited Family Trauma Shapes Who We Are and How to End the Cycle By Mark Wolynn: Key Takeaways, Summary & AnalysisFrom EverandSummary: It Didn't Start with You: How Inherited Family Trauma Shapes Who We Are and How to End the Cycle By Mark Wolynn: Key Takeaways, Summary & AnalysisRating: 5 out of 5 stars5/5 (4)
- Summary: I'm Glad My Mom Died: by Jennette McCurdy: Key Takeaways, Summary & AnalysisFrom EverandSummary: I'm Glad My Mom Died: by Jennette McCurdy: Key Takeaways, Summary & AnalysisRating: 4.5 out of 5 stars4.5/5 (2)
- The 16 Undeniable Laws of Communication: Apply Them and Make the Most of Your MessageFrom EverandThe 16 Undeniable Laws of Communication: Apply Them and Make the Most of Your MessageRating: 5 out of 5 stars5/5 (74)
- Learn Spanish While SleepingFrom EverandLearn Spanish While SleepingRating: 4 out of 5 stars4/5 (20)
- Weapons of Mass Instruction: A Schoolteacher's Journey Through the Dark World of Compulsory SchoolingFrom EverandWeapons of Mass Instruction: A Schoolteacher's Journey Through the Dark World of Compulsory SchoolingRating: 4.5 out of 5 stars4.5/5 (149)
- Learn English: Must-Know American English Slang Words & Phrases (Extended Version)From EverandLearn English: Must-Know American English Slang Words & Phrases (Extended Version)Rating: 5 out of 5 stars5/5 (30)
- The Story of the World, Vol. 1 AudiobookFrom EverandThe Story of the World, Vol. 1 AudiobookRating: 4.5 out of 5 stars4.5/5 (3)
- Summary: Trading in the Zone: Trading in the Zone: Master the Market with Confidence, Discipline, and a Winning Attitude by Mark Douglas: Key Takeaways, Summary & AnalysisFrom EverandSummary: Trading in the Zone: Trading in the Zone: Master the Market with Confidence, Discipline, and a Winning Attitude by Mark Douglas: Key Takeaways, Summary & AnalysisRating: 5 out of 5 stars5/5 (15)
- Summary: Greenlights: by Matthew McConaughey: Key Takeaways, Summary & AnalysisFrom EverandSummary: Greenlights: by Matthew McConaughey: Key Takeaways, Summary & AnalysisRating: 4 out of 5 stars4/5 (6)
- How to Improve English Speaking: How to Become a Confident and Fluent English SpeakerFrom EverandHow to Improve English Speaking: How to Become a Confident and Fluent English SpeakerRating: 4.5 out of 5 stars4.5/5 (56)
- Summary: The 5AM Club: Own Your Morning. Elevate Your Life. by Robin Sharma: Key Takeaways, Summary & AnalysisFrom EverandSummary: The 5AM Club: Own Your Morning. Elevate Your Life. by Robin Sharma: Key Takeaways, Summary & AnalysisRating: 4.5 out of 5 stars4.5/5 (22)
- Financial Feminist: Overcome the Patriarchy's Bullsh*t to Master Your Money and Build a Life You LoveFrom EverandFinancial Feminist: Overcome the Patriarchy's Bullsh*t to Master Your Money and Build a Life You LoveRating: 5 out of 5 stars5/5 (1)
- Make It Stick by Peter C. Brown, Henry L. Roediger III, Mark A. McDaniel - Book Summary: The Science of Successful LearningFrom EverandMake It Stick by Peter C. Brown, Henry L. Roediger III, Mark A. McDaniel - Book Summary: The Science of Successful LearningRating: 4.5 out of 5 stars4.5/5 (55)
- You Are Not Special: And Other EncouragementsFrom EverandYou Are Not Special: And Other EncouragementsRating: 4.5 out of 5 stars4.5/5 (6)
- Little Soldiers: An American Boy, a Chinese School, and the Global Race to AchieveFrom EverandLittle Soldiers: An American Boy, a Chinese School, and the Global Race to AchieveRating: 4 out of 5 stars4/5 (25)
- Summary of The Power of Habit: Why We Do What We Do in Life and Business by Charles DuhiggFrom EverandSummary of The Power of Habit: Why We Do What We Do in Life and Business by Charles DuhiggRating: 4.5 out of 5 stars4.5/5 (261)
- Rooted in Joy: Creating a Classroom Culture of Equity, Belonging, and CareFrom EverandRooted in Joy: Creating a Classroom Culture of Equity, Belonging, and CareNo ratings yet
- Why Smart People Hurt: A Guide for the Bright, the Sensitive, and the CreativeFrom EverandWhy Smart People Hurt: A Guide for the Bright, the Sensitive, and the CreativeRating: 3.5 out of 5 stars3.5/5 (54)
- Follow The Leader: A Collection Of The Best Lectures On LeadershipFrom EverandFollow The Leader: A Collection Of The Best Lectures On LeadershipRating: 5 out of 5 stars5/5 (122)
- Cynical Theories: How Activist Scholarship Made Everything about Race, Gender, and Identity―and Why This Harms EverybodyFrom EverandCynical Theories: How Activist Scholarship Made Everything about Race, Gender, and Identity―and Why This Harms EverybodyRating: 4.5 out of 5 stars4.5/5 (221)