Professional Documents
Culture Documents
Introduction To Column Buckling
Uploaded by
Parth ChopraOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Introduction To Column Buckling
Uploaded by
Parth ChopraCopyright:
Available Formats
A10 - Introduction to Column Buckling 1
Introduction of Column Buckling
Structures subjected to compressive (and other types o loads! may
become unstable and buckle" In ideali#ed situations$ buckling is
the sudden onset o very large displacements at some critical load
(generally transverse to the member! and sometimes %ith a
corresponding decrease in load-carrying capacity" In other
situations$ buckling may occur more gradually& but as the load
approaches the critical load displacements %ill increase at a rapid
rate" Belo% are e'amples o buckling situations(
Consider a column i'ed on one end and subjected
to a unia'ial compressive load )" *hen ) is small$
the column shortens a'ially (is compressed!"
*hen the a'ial compressive orce ) reaches a
critical value
cr
P
$ the column suddenly e'periences
a lateral displacement$ i"e"$ it buckles"
A10 - Introduction to Column Buckling +
A thin$ deep cantilever beam
is subjected to a vertical end
load )" As long as the load )
is belo% a critical value
cr
P
$
the beam section remains
vertical (motion is do%n%ard
only! and resists the bending
action o )"
At the critical value
cr
P
$ the beam
%ill t%ist and bend side%ard (out
o the vertical plane!"
,he point at %hich the structure
buckles is called an instability
point" At or just belo% the critical
value o the load$ any small disturbance can cause the structure to
change position as sho%n in the sketch o ) vs" displacement"
side%ard displacement$ t%ist
P
cr
P P
idealized
actual
A10 - Introduction to Column Buckling -
A amiliar soda can is sho%n belo%" *hen the applied load ) is
suiciently small$ the vertical %all remains cylindrical and is
compressed uniormly in the vertical direction (ig" a!"
I ) becomes too
large (reaches the
critical value!$ the
position becomes
unstable" A small
disturbance causes
the vertical %alls to
bend in and out in a
comple' pattern as
sho%n in ig" b
(buckling or
crumpling occurs!"
,he top may even rotate relative to the bottom"
A10 - Introduction to Column Buckling .
A some%hat dierent type o instability is sho%n belo% or a
shallo% curved arch or dome"
As the load )
is increased$
the top o the
arch
displaces
do%n%ard in
a some%hat
linear ashion (ig" a!"
/o%ever$ at some critical value o )$
the arch %ill suddenly snap through to
the coniguration sho%n in ig" b" ,his
is called snap buckling" At this critical
load$ the arch (top! suddenly moves
vertically rom displacement A to B
%ith 01 increase in load )"
vertical displacement
)
snap-through
A B
A10 - Introduction to Column Buckling 2
,he investigation o structural instability and buckling is a diicult
subject" *e shall consider only the case o the cantilevered
column discussed previously" Beore considering this stability
problem$ it is necessary to derive the e3uations governing the
bending o a beam subjected to longitudinal as %ell as transverse
loads" Consider a ree-body o a beam %ith a transverse load 3('!
and a constant a'ial orce ) as sho%n belo%"
P
P
x
y
( ! v x
M M +
M
P
P P +
V V +
V
x
v
( ! p x
p x
Summing orces vertically and taking moments about the center o
the dierential element yields(
A10 - Introduction to Column Buckling 4
+ +
0
( ! 0
x x
V V V p x
M M M V V V P v
+ +
+ + + + +
5ivide by x and take the limit 0 x to obtain
0
0
dV
p
dx
dM dv
V P
dx dx
+ +
Assume that the bending moment is responsible or the transverse
deormation o the beam& i"e"$ %e %ill neglect the eect o shear on
the deormations (same as 6078 +1. and A681 -0.!" ,hen$
+
+
d v
EI M
dx
Substituting into the moment e3uation gives
A10 - Introduction to Column Buckling 9
+
+
0
d d v dv
EI V P
dx dx
dx
_
+ +
,
Solving or : and substituting in the shear e3uation gives
+ +
+ +
d d v d dv
EI P p
dx dx
dx dx
_
_
+
,
,
0o% consider the cantilevered column
%ith only an a'ial compressive orce )"
Boundary conditions or this problem are
given by(
0
0
0
v
at x
dv
dx
0
0
M
at x L
V
x
y
L
P
A10 - Introduction to Column Buckling ;
,he boundary conditions at '<= may be e'pressed in terms o
v
by
substituting the boundary conditions into the second o e3uations $
and $ into to obtain(
+
+
+
+
0
0
d v
M EI
dx
at x L
d d v dv
V P
dx dx
dx
;
_
+
,
>or constant 6I and )$ the governing dierential e3uation
becomes
. +
. +
0
d v d v
EI P
dx dx
+
*e must no% ind the solution to the dierential e3uation subject
to the boundary conditions at '<0 ?e3" @ and '<= ?e3" @" *e note
that v<0 is a solution or any value o )" /o%ever$ %e are not
A10 - Introduction to Column Buckling A
interested in this trivial solution" ,he theory o dierential
e3uations states that %e must have . independent constants in the
general solution to the dierential e3uation (there are . boundary
conditions!" A possible solution or
( ! v x
is a combination o
polynomial and trigonometric terms(
1 + - .
( ! sin cos
P P
v x c c x c x c x
EI EI
+ + +
Bou can veriy that this assumed solution satisies the dierential
e3uation" Substituting into the . boundary conditions ?+ boundary
conditons at '<0 in and + at '<= in @ gives the ollo%ing(
A10 - Introduction to Column Buckling 10
1 .
+ -
- .
+
0
0
sin cos 0
0
c c
P
c c
EI
P P P P
c L c L
EI EI EI EI
c P
+
+
0ote that all the right-hand sides are e3ual to 0& hence$ a possible
solution is that
1 + - .
0 c c c c
" In this case$
( ! 0 v x
is the
solution or e3uilibrium o the cantilevered column" ,his %ould
correspond to simple compression o the column %ith no side%ays
motion" /o%ever$ %e consider this once again a trivial solution"
*e need to ind another solutionC
63uations are in act an eigenvalue problemC
A10 - Introduction to Column Buckling 11
1
+
-
.
1 0 0 1
0
0 1 0
0
0
0 0 sin cos
0
0 0 0
c
P
c
EI
c
P P P P
L L
c
EI EI EI EI
P
1
1
1
1
' ; ' ;
1
1
1
1
]
,he solution o the eigenvalue problem re3uires that the
determinant o the .'. coeicient matri' by e3ual to #ero %hich
%ill yield the solution or ) satisying this condition" 0ote that %e
%ill obtain an ininite number o solutions due to the repeating
nature o the sin and cos trigonometric unctions" An easier
approach is as ollo%s" 8eerring to e3uation $ the ourth e3uation
implies that
+
0 c
is a possible solution (or 0 P !" *ith
+
0 c
$
the second e3uation implies that
-
0 c
is a possible solution" ,he
irst e3uation implies that
. 1
c c
" /ence$ the third e3uation
becomes simply(
A10 - Introduction to Column Buckling 1+
1
cos 0
P P
c L
EI EI
,he last e3uation can be satisied by setting
1
0 c
$ %hich is a
trivial solution again$ or by having a value o ) such that
cos 0
P
L
EI
,he smallest value o ) satisying this condition is
+
+
.
EI
P
L
Substituting this value o ) back into
( ! v x
gives
1
( ! 1 cos
+
x
v x c
L
_
,
A10 - Introduction to Column Buckling 1-
/ence$ %e have ound the critical value o )$ and the shape that the
beam bends into or this critical load" 0ote that the value o
1
c
cannot be determined" ,his is the nature o an eigenvalue problem"
Since the solution o an eigenvalue problem re3uires that %e orce
the determinant o the coeicient matri' to be e3ual to #ero$ this is
e3uivalent to making the e3uations linearly dependent" =inearly
dependent e3uations can only be solved by assuming a solution or
one (or more! o the unkno%ns (cDs in this case!& and the solution
%ill al%ays be in terms o the assumed c value" 0ote that %hen
cr
P P <
$ the transverse delection is #ero" ,ransverse delection
occurs only %hen
cr
P P
"
/ence$ %e have or the cantilevered column the critical value o )(
+
+
( !
.
cr
EI
P for cantilevered column
L
>or other end conditions$ %e can ollo% the same procedure to
obtain(
A10 - Introduction to Column Buckling 1.
A10 - Introduction to Column Buckling 12
>or a'ial loads that are not perectly centered$ %e obtain an
entirely dierent result" Consider the case %hen ) is oset by an
amount
(
,he problem may be %orked as beore$ e'cept that %e treat the
problem as having a perectly centered load ) plus a moment
o
M P
as sho%n above" *e ind that the third boundary
condition in e3uations is modiied so that the right-hand side is
e3ual to
E
o
M EI
" >ollo%ing the same procedure$ %e ind that the
transverse delection is given by(
x
y
L
P
x
y
L
P
=
o
M P
A10 - Introduction to Column Buckling 14
sec 1 sec 1
o
M P P
L L
P EI EI
_ _
, ,
)lotting ) vs" gives the plot on
the right" >or small values o )$ the
transverse delection is very nearly
#ero" >or e'ample$ < %hen
.
A
crit
P P <
%here
+
+
.
crit
EI
P
L
is
the value obtained or a perectly
centered load ) on a cantilevered
column" As ) approaches the
critical load$ the delection
becomes very large" Because a'ial
orces are rarely perectly centered$
one %ill al%ays ind some amount
o transverse delection occurring beore ) reaches the critical
load"
You might also like
- Part I: Rotational vs. Irrotational Flow, Circulation, Stream Function, Potential FlowDocument5 pagesPart I: Rotational vs. Irrotational Flow, Circulation, Stream Function, Potential FlowgarridolopezNo ratings yet
- Particle in A 1D BoxDocument4 pagesParticle in A 1D BoxJaisurya NanduriNo ratings yet
- Problems in Quantum Mechanics: Third EditionFrom EverandProblems in Quantum Mechanics: Third EditionRating: 3 out of 5 stars3/5 (2)
- Topic 3Document8 pagesTopic 3Fakhrul Izzuddin RozaliNo ratings yet
- Coning Angle HoverDocument2 pagesConing Angle HovermanitheaerialfighterNo ratings yet
- ME311 061 Chapter6Document6 pagesME311 061 Chapter6AhmedAliNo ratings yet
- Coning Angle Forward FlightDocument3 pagesConing Angle Forward FlightmanitheaerialfighterNo ratings yet
- Biaxial Columns DesignDocument14 pagesBiaxial Columns DesignVinayak PotdarNo ratings yet
- AE3010 Aerodynamics and Propulsion: Dr. Peter Barrington RV219 P.barrington@kingston - Ac.ukDocument55 pagesAE3010 Aerodynamics and Propulsion: Dr. Peter Barrington RV219 P.barrington@kingston - Ac.ukSabine BroschNo ratings yet
- Lecture3 5 PDFDocument39 pagesLecture3 5 PDFverbicarNo ratings yet
- Basic Assumptions and Equations in Fluid MechanicsDocument5 pagesBasic Assumptions and Equations in Fluid MechanicsMarius RosuNo ratings yet
- Lecture 11 Two Degree of Freedom ModelDocument10 pagesLecture 11 Two Degree of Freedom ModelBijay Kumar MohapatraNo ratings yet
- Chapter 3-1Document34 pagesChapter 3-1Eng-Mohammed KayedNo ratings yet
- B.R. Duffy and H.K. Moffatt - A Similarity Solution For Viscous Source Flow On A Vertical PlaneDocument11 pagesB.R. Duffy and H.K. Moffatt - A Similarity Solution For Viscous Source Flow On A Vertical PlaneVortices3443No ratings yet
- Variational Beam Theory: X y V (X)Document2 pagesVariational Beam Theory: X y V (X)Ronnie BoutilierNo ratings yet
- Torsion and Transverse Shear of Thin-Walled BeamsDocument54 pagesTorsion and Transverse Shear of Thin-Walled BeamsproradexNo ratings yet
- Topic 17 Blasius SolutionDocument11 pagesTopic 17 Blasius SolutionMohammad GhasemiNo ratings yet
- ME2135 Part 2 Sample Questions - Q20Document6 pagesME2135 Part 2 Sample Questions - Q20huykhang.tranpNo ratings yet
- Statement of The ProblemDocument7 pagesStatement of The ProblemShootingStarPhotonsNo ratings yet
- Plane Electromagnetic Wave The Helmhotz Equation:: E H E H E E E E H E E E E E EDocument12 pagesPlane Electromagnetic Wave The Helmhotz Equation:: E H E H E E E E H E E E E E EVinay KumarNo ratings yet
- Trend, Variation, and Universal KrigingDocument12 pagesTrend, Variation, and Universal KrigingAdrian Hanenda QadarismanNo ratings yet
- Combining Error Ellipses: John E. DavisDocument17 pagesCombining Error Ellipses: John E. DavisAzem GanuNo ratings yet
- LECTURE 2 - Fluid DynamicsDocument13 pagesLECTURE 2 - Fluid DynamicsBang AnuhNo ratings yet
- Transversal It yDocument8 pagesTransversal It ysorialoloNo ratings yet
- SPM Add Maths Formula List Form5Document28 pagesSPM Add Maths Formula List Form5Sayantani GhoshNo ratings yet
- Some General Solutions and Theorems Pertaining To The Creeping Motion EquationsDocument38 pagesSome General Solutions and Theorems Pertaining To The Creeping Motion Equationsdaniel.jiao2019No ratings yet
- Fundamentals of Structural Geology Exercise: Concepts From Chapter 10Document5 pagesFundamentals of Structural Geology Exercise: Concepts From Chapter 10firstdawn02No ratings yet
- Del OperatorDocument6 pagesDel OperatorSupriya Aggarwal100% (1)
- Subject: Arch315-Strength of MaterialsDocument15 pagesSubject: Arch315-Strength of MaterialsAlyssa MadelNo ratings yet
- Docarmo ErratasDocument7 pagesDocarmo ErratasRicardo E.No ratings yet
- Lecture 10 - Integrating Vector FunctionsDocument15 pagesLecture 10 - Integrating Vector FunctionsnguyenyenthanhbtNo ratings yet
- Laminar Boundary Layer On Oscillating Plates and CylindersDocument14 pagesLaminar Boundary Layer On Oscillating Plates and CylindersSafaa Hameed Al NaseryNo ratings yet
- 3-7 Fluids in Rigid-Body Motion: - We ObtainedDocument6 pages3-7 Fluids in Rigid-Body Motion: - We ObtainedAsmaa Ali El-AwadyNo ratings yet
- Problem Set 6 Problem 1.: R B B P T I Ikz R V VDocument2 pagesProblem Set 6 Problem 1.: R B B P T I Ikz R V VmkpsrtmNo ratings yet
- College Physics: Phys 111 Dr. Tribble Summary Material On FluidsDocument6 pagesCollege Physics: Phys 111 Dr. Tribble Summary Material On FluidsEL Jann MalbuyoNo ratings yet
- 1 Continuous Laplacian (Diffusive) Growth PhenomenaDocument10 pages1 Continuous Laplacian (Diffusive) Growth PhenomenaLameuneNo ratings yet
- Chapter 6Document37 pagesChapter 6ceice2013No ratings yet
- Linear EquationDocument12 pagesLinear EquationaassmmrrNo ratings yet
- Dixon SystemsDocument15 pagesDixon SystemsSteve Thomas ForsterNo ratings yet
- Chapter8 Latest Combined ComplejoDocument49 pagesChapter8 Latest Combined ComplejoLuis Carlos Gonzales RengifoNo ratings yet
- Introduction To Conformal Mapping in Aerodynamics: Z Real + I Imaginary X + I yDocument8 pagesIntroduction To Conformal Mapping in Aerodynamics: Z Real + I Imaginary X + I ykarthipriyaNo ratings yet
- Two-Dimensional Airfoils: 1 DefinitionsDocument5 pagesTwo-Dimensional Airfoils: 1 DefinitionsKing MassNo ratings yet
- 6.5 The Saddle Point Stokes ProblemDocument8 pages6.5 The Saddle Point Stokes ProblemEfstathios SiampisNo ratings yet
- Ground Water ModellingDocument10 pagesGround Water ModellingAllen KurniawanNo ratings yet
- 6.5 The Saddle Point Stokes ProblemDocument8 pages6.5 The Saddle Point Stokes ProblemEfstathios SiampisNo ratings yet
- Potential Flow Around A Circular CylinderDocument4 pagesPotential Flow Around A Circular CylinderGanesh NandgaonkarNo ratings yet
- Ch05 Lecture (C)Document35 pagesCh05 Lecture (C)Gabriel FabrícioNo ratings yet
- Conformal Mapping: Magnetic Field Problems, 2nd Edition, Pergamon Press, New York 1973Document9 pagesConformal Mapping: Magnetic Field Problems, 2nd Edition, Pergamon Press, New York 1973subha_aeroNo ratings yet
- Chapter 14: Polar Weather: Katabatic WindsDocument13 pagesChapter 14: Polar Weather: Katabatic WindsAndika B CandraNo ratings yet
- Jackson 11 3 Homework SolutionDocument2 pagesJackson 11 3 Homework SolutionJohn HolmanNo ratings yet
- Jackson 11 3 Homework SolutionDocument2 pagesJackson 11 3 Homework SolutionAbdul Shakoor ButtNo ratings yet
- Nlewis65 338 343 Classroom Iveson 34 No 4 Fall 2000 CeeDocument6 pagesNlewis65 338 343 Classroom Iveson 34 No 4 Fall 2000 CeeBATTINA MURALINo ratings yet
- Regression 29: y A + BXDocument1 pageRegression 29: y A + BXChipo ChipNo ratings yet
- 2021 LF Final ExamDocument3 pages2021 LF Final Examfajar anggaraNo ratings yet
- 6 Stability: 6.1 Stability of A Point in Phase SpaceDocument8 pages6 Stability: 6.1 Stability of A Point in Phase Spacezcapg17No ratings yet
- Class23 Lorentz 1Document23 pagesClass23 Lorentz 1SupriyoNaskarNo ratings yet
- Elastic Stability of ColumnsDocument11 pagesElastic Stability of ColumnsSayantan GhosalNo ratings yet
- LaSalle's Invariance Principle & Chetaev's TheoremDocument5 pagesLaSalle's Invariance Principle & Chetaev's TheoremMutt3012No ratings yet
- Insurcent: Team Orange/#3Document10 pagesInsurcent: Team Orange/#3Parth ChopraNo ratings yet
- 3D Reconstruction From Two 2D Images Ted Shultz and Luis A. RodriguezDocument14 pages3D Reconstruction From Two 2D Images Ted Shultz and Luis A. RodriguezParth ChopraNo ratings yet
- Truth Tables ShortDocument2 pagesTruth Tables ShortParth ChopraNo ratings yet
- Computer Vision Nanodegree Syllabus: Before You StartDocument5 pagesComputer Vision Nanodegree Syllabus: Before You StartCristi PopaNo ratings yet
- Outline of This Talk: - Data AssociationDocument61 pagesOutline of This Talk: - Data AssociationParth ChopraNo ratings yet
- Document v2Document11 pagesDocument v2Parth ChopraNo ratings yet
- UMich Transcript Submission FormDocument1 pageUMich Transcript Submission FormParth ChopraNo ratings yet
- Mess Receipt - FebDocument1 pageMess Receipt - FebParth ChopraNo ratings yet
- Sales Docket PreviewDocument1 pageSales Docket PreviewParth ChopraNo ratings yet
- TOEFL ReceiptDocument2 pagesTOEFL ReceiptParth ChopraNo ratings yet
- Sales Docket PreviewDocument1 pageSales Docket PreviewParth ChopraNo ratings yet
- DTU EP Syllabus PDFDocument63 pagesDTU EP Syllabus PDFParth Chopra100% (1)
- Geography Group ActivityDocument7 pagesGeography Group ActivityParth ChopraNo ratings yet
- Mess Receipt - FebDocument1 pageMess Receipt - FebParth ChopraNo ratings yet
- Aptitude TestDocument10 pagesAptitude TestParth ChopraNo ratings yet
- Mission Simulation Timing: No. of Full Mission SimulationsDocument1 pageMission Simulation Timing: No. of Full Mission SimulationsParth ChopraNo ratings yet
- Information Technology in EducationDocument6 pagesInformation Technology in EducationParth ChopraNo ratings yet
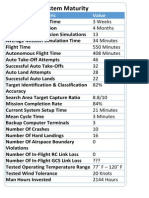
- System ReadinessmaturityDocument1 pageSystem ReadinessmaturityParth ChopraNo ratings yet
- EconomicsDocument2 pagesEconomicsParth ChopraNo ratings yet
- Document Yiga 2Document1 pageDocument Yiga 2Parth ChopraNo ratings yet
- Document123 443dsdfDocument2 pagesDocument123 443dsdfParth ChopraNo ratings yet
- Payload Drop Calculation GUIDocument1 pagePayload Drop Calculation GUIParth ChopraNo ratings yet
- Economics in Daily LifeDocument2 pagesEconomics in Daily LifeParth ChopraNo ratings yet
- Civil Services 2014 AdvertisementDocument44 pagesCivil Services 2014 AdvertisementPradeep SharmaNo ratings yet
- Component List - APM ConfigDocument1 pageComponent List - APM ConfigParth ChopraNo ratings yet
- Component List - Airware ConfigDocument1 pageComponent List - Airware ConfigParth ChopraNo ratings yet
- Spar LocationDocument4 pagesSpar LocationParth ChopraNo ratings yet
- Tut02 MouseDocument99 pagesTut02 MouseUmut ArslanNo ratings yet
- Manufacturing and Struct. Analysis of A UAVDocument129 pagesManufacturing and Struct. Analysis of A UAVsaifchi555No ratings yet
- Rohacell ADocument6 pagesRohacell AParth ChopraNo ratings yet