Paper Reference(s)

6663

Edexcel GCE
Core Mathematics C1 Advanced Subsidiary
Monday 10 January 200 A!ternoon "ime# 1 hour 30 minutes

Materials re$uired !or examination Mathematical Formulae (Green)

%tems included &ith $uestion 'a'ers Nil

Calculators may ()" be used in this examination*

%nstructions to Candidates In the boxes on the answer book, write the name of the examining bo ! (" excel), !our centre number, can i ate number, the unit title (#ore Mathematics #$), the paper reference (%%%&), !our surname, initials an signature' %n!ormation !or Candidates ( booklet )Mathematical Formulae an *tatistical +ables, is pro-i e ' Full marks ma! be obtaine for answers to (.. /uestions' +his paper has ten /uestions' +he total mark for this paper is 01' Advice to Candidates 2ou must ensure that !our answers to parts of /uestions are clearl! labelle ' 2ou must show sufficient working to make !our metho s clear to the "xaminer' (nswers without working ma! gain no cre it'

(23+,0A

+his publication ma! onl! be repro uce in accor ance with .on on 3ualifications cop!right polic!' 45661 .on on 3ualifications .imite '

1*

(a) 7rite own the -alue of $% 5 ' -1. (b) Fin the -alue of $% 5 ' -2.
&

2*

(i) Gi-en that y 8 1x& 9 0x 9 &, fin (a)

y , x

-3.
5

(b)

x5

' -1.

$ (ii) Fin $ + & x 5 x' x

-+. 3* Gi-en that the e/uation kx5 9 $5x 9 k 8 6, where k is a positi-e constant, has e/ual roots, fin the -alue of k' -+.

+*

*ol-e the simultaneous e/uations x9y85 x5 9 5y 8 $5' -6.

+he rth term of an arithmetic series is (5r : 1)' (a) 7rite own the first three terms of this series' -2. (b) *tate the -alue of the common ifference' -1. (c) *how that

(5r 1)
r =$

8 n(n : ;)' -3.

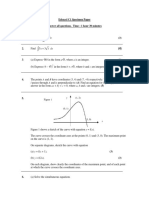
6* y

/i0ure 1

5 P(&, :5)

Figure $ shows a sketch of the cur-e with e/uation y 8 f(x)' +he cur-e crosses the x<axis at the points (5, 6) an (;, 6)' +he minimum point on the cur-e is P(&, :5)' In separate iagrams sketch the cur-e with e/uation (a) y 8 :f(x), -3. (b) y 8 f(5x)' -3. =n each iagram, gi-e the coor inates of the points at which the cur-e crosses the x<axis, an the coor inates of the image of P un er the gi-en transformation'
1 x , x 6' +he point P on C has x<coor inate $' x

1*

+he cur-e C has e/uation y 8 ;x5 9 (a) *how that the -alue of

y at P is &' x

- . (b) Fin an e/uation of the tangent to C at P' -3. +his tangent meets the x<axis at the point (k, 6)' (c) Fin the -alue of k' -2.

N5&;>6(

&

2* y A($, 0)

/i0ure 2 B(56, 0)

D(?, 5) O C( p, q) +he points A($, 0), B(56, 0) an C( p, q) form the -ertices of a triangle ABC, as shown in Figure 5' +he point D(?, 5) is the mi <point of AC' (a) Fin the -alue of p an the -alue of q' -2. +he line l, which passes through D an is perpen icular to AC, intersects AB at E' (b) Fin an e/uation for l, in the form ax 9 by 9 c 8 6, where a, b an c are integers' - . (c) Fin the exact x<coor inate of E' -2. ,* +he gra ient of the cur-e C is gi-en b!
y 8 (&x : $)5' x

+he point P($, ;) lies on C' (a) Fin an e/uation of the normal to C at P' -+. (b) Fin an e/uation for the cur-e C in the form y 8 f(x)' - .

N5&;>6(

(c) @sing

y 8 (&x : $)5, show that there is no point on C at which the tangent is parallel to the x

line y 8 $ : 5x' -2. 10* Gi-en that f(x) 8 x5 : %x 9 $?, x 6, -3. +he cur-e C with e/uation y 8 f(x), x 6, meets the y<axis at P an has a minimum point at Q' (b) *ketch the graph of C, showing the coor inates of P an Q' -+. +he line y 8 ;$ meets C at the point R' (c) Fin the x<coor inate of R, gi-ing !our answer in the form p 9 q5, where p an q are integers' - . ")"A3 /)4 5A5E4# 1 MA46S E(7

(a) express f(x) in the form (x : a)5 9 b, where a an b are integers'

N5&;>6(