Professional Documents
Culture Documents
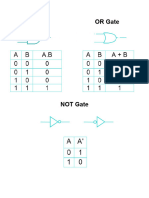
Boolean Algebra
Boolean Algebra
Uploaded by
balajimetturCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Boolean Algebra
Boolean Algebra
Uploaded by
balajimetturCopyright:
Available Formats
Laws and Theorems of Boolean Algebra
Operations with 0 and 1:
1.
2.
X+0=X
X+1=1
1D.
2D.
X1=X
X0=0
3D.
XX=X
5D.
X X' = 0
6D.
XY=YX
7D.
(XY)Z = X(YZ) = XYZ
8D.
X + YZ = ( X + Y ) ( X + Z )
9D.
10D.
11D.
( X + Y ) ( X + Y' ) = X
X(X+Y)=X
XY' + Y = X + Y
12D.
(X Y Z )' = X' + Y' + Z' +
Idempotent laws
3.
X+X=X
Involution law:
4.
( X' ) ' = X
Laws of complementarity:
5.
X + X' = 1
Commutative laws:
6.
X+Y=Y+X
Associative laws:
7.
(X + Y) + Z = X + (Y + Z)
=X+Y+Z
Distributive laws:
8.
X( Y + Z ) = XY + XZ
Simplification theorems:
9.
10.
11.
X Y + X Y' = X
X + XY = X
( X + Y' ) Y = XY
DeMorgans laws:
12.
( X + Y + Z + )' = X'Y'Z'
13.
[ f ( X1, X2, XN, 0, 1, +, ) ]' = f ( X1', X2', XN', 1, 0, , + )
Duality:
14.
( X + Y + Z + )D = X Y Z
15.
[ f ( X1, X2, XN, 0, 1, +, ) ] D = f ( X1, X2, XN, 1, 0, , + )
14D.
(X Y Z)D = X + Y + Z +
Theorem for multiplying out and factoring:
16.
( X + Y ) ( X' + Z ) = X Z + X' Y
16D.
XY + X' Z = ( X + Z ) ( X' + Y )
17D.
(X + Y)(Y + Z)(X' + Z)
= (X + Y)(X' + Z)
Consensus theorem:
17.
XY + YZ + X'Z = XY + X'Z
You might also like
- Assignment 3 SolutionsDocument7 pagesAssignment 3 SolutionsNengke Lin100% (1)
- Metric SpacesDocument20 pagesMetric Spacesatiq4pk75% (8)
- Functional AnalysisDocument71 pagesFunctional AnalysisMera NomanNo ratings yet
- Math 135-2, Homework 1: Problem 17.1Document11 pagesMath 135-2, Homework 1: Problem 17.1Jean PierreNo ratings yet
- Practical Scientific Computing in Python A WorkbookDocument43 pagesPractical Scientific Computing in Python A WorkbookJeff PrattNo ratings yet
- BooleanDocument8 pagesBooleanapi-3757260No ratings yet
- Boolean TheoremsDocument6 pagesBoolean TheoremsfgkloNo ratings yet
- CS302 2005 2010 Midterm - Solved - MEGA FILEDocument91 pagesCS302 2005 2010 Midterm - Solved - MEGA FILEattiqueNo ratings yet
- CS302 2005 2010 Midterm - Solved - MEGA FILEDocument91 pagesCS302 2005 2010 Midterm - Solved - MEGA FILEAli QureshiNo ratings yet
- Cs33 - Data Structures Questions and AnswersDocument26 pagesCs33 - Data Structures Questions and Answerssri1bhu288% (43)
- Quiz Questions For DLD LabDocument6 pagesQuiz Questions For DLD LabGerald Carson100% (1)
- C ProgrammingDocument14 pagesC ProgrammingSakib MuhaiminNo ratings yet
- Morris Mano ch01Document25 pagesMorris Mano ch01Praveen DhawanNo ratings yet
- Automata Theory Midterm Exam SolutionDocument5 pagesAutomata Theory Midterm Exam SolutionFernando EsparzaNo ratings yet
- Error Detection and Correction Using Hamming CodeDocument55 pagesError Detection and Correction Using Hamming CodeArunabh Nag75% (8)
- Digital Electronics Ec 1201Document34 pagesDigital Electronics Ec 1201ainugiri100% (1)
- Objective Questions of Discrete MathematicsDocument120 pagesObjective Questions of Discrete MathematicsJagdish Kapadnis68% (28)
- Object Oriented Programming: Unit - I PART - A (Short Answer Question) (Class Test 1)Document6 pagesObject Oriented Programming: Unit - I PART - A (Short Answer Question) (Class Test 1)Anonymous BOreSFNo ratings yet
- Partial DerivativesDocument91 pagesPartial Derivativesrafqi17No ratings yet
- Theory of Computation Solved MCQ - Part 2 - Computer Science Solved MCQsDocument8 pagesTheory of Computation Solved MCQ - Part 2 - Computer Science Solved MCQsAdithya TaNo ratings yet
- Lecture Notes - TOCDocument18 pagesLecture Notes - TOCrmidhunajyothiNo ratings yet
- Finite State Machine ExamplesDocument55 pagesFinite State Machine ExamplesDionisio De Zolt100% (2)
- Moore and Mealy MachinesDocument6 pagesMoore and Mealy MachinesNirmal Kumar PandeyNo ratings yet
- SlideSet 14Document74 pagesSlideSet 14Rumaan AliNo ratings yet
- Boolean AlgebraDocument25 pagesBoolean AlgebraTejas Bhandari100% (6)
- Boolean Algebra Laws Cheat Sheet: by ViaDocument1 pageBoolean Algebra Laws Cheat Sheet: by ViaShikin AinNo ratings yet
- Laws of Boolean AlgebraDocument1 pageLaws of Boolean AlgebraDarshanNo ratings yet
- Summary of Laws and TheormsDocument1 pageSummary of Laws and Theormsআব্দুল্লাহ আল ইমরানNo ratings yet
- Teoremas de BooleDocument1 pageTeoremas de BooleYulissa Mendoza SalgadoNo ratings yet
- Course: Electronic Engineering UEC001: Topic: Boolean AlgebraDocument21 pagesCourse: Electronic Engineering UEC001: Topic: Boolean AlgebraAaryan TandonNo ratings yet
- 2.1.5a BooleanDeMorganTheoremsDocument2 pages2.1.5a BooleanDeMorganTheoremsTyree FranklinNo ratings yet
- Boolean AlgebraDocument53 pagesBoolean AlgebraDEBANGAN GANGULYNo ratings yet
- Boolean Theorem Penned by Faisal HaroonDocument3 pagesBoolean Theorem Penned by Faisal HaroonFaisal HaroonNo ratings yet
- EE/CE 6301: Advanced Digital LogicDocument20 pagesEE/CE 6301: Advanced Digital LogicspoortipNo ratings yet
- Boolean AlgebraDocument20 pagesBoolean Algebrafernando vargasNo ratings yet
- Week 4 Boolean Algebra Part-1 - 2021Document52 pagesWeek 4 Boolean Algebra Part-1 - 2021Kelvin Putra UtamaNo ratings yet
- Digital Logic DesignDocument4 pagesDigital Logic DesignAkshay KumarNo ratings yet
- Lec 5Document31 pagesLec 5Ahmet ArabNo ratings yet
- Tutorial #2Document31 pagesTutorial #2Arnav ChaturvediNo ratings yet
- Trigonometrijske Jednakosti: X y X y X y X y X y X yDocument1 pageTrigonometrijske Jednakosti: X y X y X y X y X y X ySulejmanNo ratings yet
- Boolean AlgebraDocument5 pagesBoolean AlgebraSyste DesigNo ratings yet
- Real Analysis Homework SolutionsDocument2 pagesReal Analysis Homework Solutionsjc224No ratings yet
- Boolean AlgebraDocument25 pagesBoolean AlgebraClaudiuNo ratings yet
- @M @y @N @X @M @y @N @XDocument3 pages@M @y @N @X @M @y @N @XSemih ÇınarNo ratings yet
- Let X Be As Set and Define D: X × X R by D (X, X) 0 X X and D (X, Y) 1, X 6 y X - Prove That D Is A Metric On XDocument9 pagesLet X Be As Set and Define D: X × X R by D (X, X) 0 X X and D (X, Y) 1, X 6 y X - Prove That D Is A Metric On XGie LiangNo ratings yet
- List of Formulas of CalculusDocument13 pagesList of Formulas of Calculusbimochandhungel57No ratings yet
- Numerical Integration CH 6Document5 pagesNumerical Integration CH 6Coder DNo ratings yet
- UNIT3 - Boolean Algebra (Continued) PDFDocument20 pagesUNIT3 - Boolean Algebra (Continued) PDF최인아No ratings yet
- Quotient RuleDocument6 pagesQuotient RuleAnaNo ratings yet
- L 11 Circle Drawing Algorithims 2Document6 pagesL 11 Circle Drawing Algorithims 2Tahesin TNo ratings yet
- Greatest Integer FunctionDocument6 pagesGreatest Integer FunctionKushal ParikhNo ratings yet
- Tma4140 Mock-Exam 2022 SolutionsDocument16 pagesTma4140 Mock-Exam 2022 Solutionssamsonhatyoka100No ratings yet
- Orddiffsoln 1997Document9 pagesOrddiffsoln 1997Graham MooreNo ratings yet
- Differentiation Formulas & Rules - Various Derivative Formulas of Trigonometric, Hyperbolic, Logarithmic & MoreDocument4 pagesDifferentiation Formulas & Rules - Various Derivative Formulas of Trigonometric, Hyperbolic, Logarithmic & Moreambresh.09No ratings yet
- Unit 03 Differential EquationsDocument5 pagesUnit 03 Differential EquationsAshok PradhanNo ratings yet
- Stochastic Hydrology: Indian Institute of ScienceDocument52 pagesStochastic Hydrology: Indian Institute of ScienceJames K. KirahukaNo ratings yet
- Differential Calculus BOOKDocument264 pagesDifferential Calculus BOOKAbdul Halil AbdullahNo ratings yet
- Module 1 Part 2Document63 pagesModule 1 Part 2matey.tushar5646No ratings yet
- Midterm On Oct 13Document31 pagesMidterm On Oct 13Tina ChenNo ratings yet
- CSE204Document5 pagesCSE204Robiul Haque BhuyanNo ratings yet
- MAT060 12 Differential Notation and Trigonometric FunctionsDocument52 pagesMAT060 12 Differential Notation and Trigonometric FunctionsShine Ibarra AlabaNo ratings yet
- The Rules of Analytical ReadingDocument1 pageThe Rules of Analytical ReadingJeff PrattNo ratings yet
- The Sheaf of A GleanerDocument112 pagesThe Sheaf of A GleanerJeff PrattNo ratings yet
- What Is The Mass of A Photon?Document3 pagesWhat Is The Mass of A Photon?Jeff Pratt100% (1)
- Street Fighting MathematicsDocument153 pagesStreet Fighting MathematicsJeff Pratt100% (1)
- Economic Science and The: Austrian MethodDocument91 pagesEconomic Science and The: Austrian MethodyqamiNo ratings yet
- Ozymandias: Percy Bysshe ShelleyDocument1 pageOzymandias: Percy Bysshe ShelleyJeff Pratt100% (1)
- National Federation of Independent Business v. SebeliusDocument193 pagesNational Federation of Independent Business v. SebeliusCasey SeilerNo ratings yet
- Ron Paul "Plan To Restore America": Executive SummaryDocument11 pagesRon Paul "Plan To Restore America": Executive SummaryJeff PrattNo ratings yet
- Scrum Guide - 2011Document17 pagesScrum Guide - 2011Angelo AssisNo ratings yet
- KarpDocument19 pagesKarpMikKeOrtizNo ratings yet
- The Evolution of LispDocument109 pagesThe Evolution of LispJeff Pratt100% (2)
- OzymandiasDocument1 pageOzymandiasJeff PrattNo ratings yet
- Agent Oriented ProgrammingDocument42 pagesAgent Oriented ProgrammingJeff PrattNo ratings yet
- ws3 1 HundtDocument10 pagesws3 1 HundtColin CarrNo ratings yet
- The Five Orders of IgnoranceDocument4 pagesThe Five Orders of IgnoranceJeff PrattNo ratings yet
- Notes On Estimation and Retrospective EstimationDocument14 pagesNotes On Estimation and Retrospective EstimationJeff PrattNo ratings yet
- Exploring LiftDocument289 pagesExploring LiftJeff PrattNo ratings yet
- Software Eng Nato1968 PDFDocument136 pagesSoftware Eng Nato1968 PDFEddy PrahastaNo ratings yet
- The Constitution of The United StatesDocument21 pagesThe Constitution of The United StatesJeff PrattNo ratings yet
- Domain Driven Design - Step by StepDocument34 pagesDomain Driven Design - Step by StepLuke Vindicare0% (1)
- If The IRS Had Discovered The Quadratic FormulaDocument1 pageIf The IRS Had Discovered The Quadratic FormulaJeff PrattNo ratings yet
- Kleisli Arrows of Outrageous FortuneDocument14 pagesKleisli Arrows of Outrageous FortuneJeff PrattNo ratings yet
- Frangipani: A Scalable Distributed File SystemDocument14 pagesFrangipani: A Scalable Distributed File SystemJeff PrattNo ratings yet
- The Quest For Cosmic JusticeDocument3 pagesThe Quest For Cosmic JusticeJeff Pratt100% (1)
- Modular Elliptic Curves and Fermat S Last Theorem by Andrew WillesDocument109 pagesModular Elliptic Curves and Fermat S Last Theorem by Andrew WillesJonnny B. GoodeNo ratings yet
- Adult PrinciplesDocument1 pageAdult PrinciplesJeff PrattNo ratings yet
- From Dictatorship To DemocracyDocument101 pagesFrom Dictatorship To DemocracySochenda KhemNo ratings yet