Atomic Term Symbols

From a spectroscopic perspective, we need to know the values

for the various types of angular momenta. Term symbols
provide three pieces of information
1. Total orbital angular momentum, L
2. Multiplicity of the term, 2S+1
3. Total angular momentum, J
2 S+1

LJ

Atomic Term Symbols

v
L Total

v
L2
v
L1

Imagine then summing these vectors together. We can do it,

but it is far easier to consider z-components as these add
together as scalars!

Atomic Term Symbols

In terms of z-components

Ml = ml1 + ml 2 + ml3 + ....

Or in terms of magnitudes

L = l1 + l 2 + l 3 + ....
The total # or series of possible values for all orientations is
given by the Clebsch-Gordon Series. For an atom with
two electrons,

L = l 1 + l 2 , l 1 + l 2 1, l 1 + l 2 2,... l 1 l 2

Atomic Term Symbols

L = l 1 + l 2 , l 1 + l 2 1, l 1 + l 2 2,... l 1 l 2
Maximum L corresponds to

l1 + l 2

Minimum L corresponds to

l1 l 2

Quantum Number L designations are

L:

0
S

1
P

2
D

3
F

4
G

Atomic Term Symbols

How does this work then for an atom with an electron
configuration with np2 (e.g., 1s2,2s22p2 or
1s22s22p63s23p2)?

L = l1 + l 2 , l1 + l 2 1, l1 + l 2 2,...l1 l 2
L = 2, 1, 0
Thus potential terms are D, P, S and each of these
terms will differ in energy.

Atomic Term Symbols

Multiplicity
Can also determine the multiplicity for the term using a
Clebsch-Gordon series
S=+,-
= 1, 0

for two electron system

Multiplicity given by 2S + 1
For S =1: 2S+1 = 3
For S=0: 2S+1 = 1

Called a triplet state

Called a singlet state

Atomic Term Symbols

Total Angular Momentum
Permitted values of J again, given by a Clebsch-Gordon series
J = L + S, L + S - 1, L + S - 2 . |L - S|

Atomic Term Symbols

As a first example, lets consider the hydrogen atom
For case with L = 1, S =
term symbols are

2P
3/2

J = 1 + and 1 -
and 2P1/2

Atomic Term Symbols

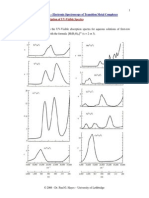
A portion of the hydrogen atom transition level diagram for
optical spectra then, will look like

2S
1/2

3s

2P
3/2
2P
1/2

2P
3/2
2S
1/2

2S
1/2

2s

1s

2P
1/2

3p
3p
2p
2p

2D

5/2

2D

3d

3/2

}spin-orbit

3d

coupling

Selection rules for optical

transitions

J = 0,1
l = 1
s = 0

Atomic Term Symbols

A portion of the hydrogen atom transition level diagram for
optical spectra then, will look like

2S
1/2

3s

2P
3/2
2P
1/2

2P
3/2
2S
1/2

2S
1/2

2s

1s

2P
1/2

3p
3p
2p
2p

2D

5/2

2D

3d

3/2

}spin-orbit

3d

coupling

Selection rules for optical

transitions

J = 0,1
l = 1
s = 0

Atomic Term Symbols

Lets look at some other examples. What is the term for the
ground state of helium? (1s2)
Here

L=0 (why?)
S=0 (why?)
Term then is 1So.

Atomic Term Symbols

What about Ne?
For 2p6 configuration, only one set of possible values.
ML= m1 + m2 + m3 + m4 + m5 + m6
= 1 + 1 + 0 + 0 + (-1) + (-1) = 0
And in this case we also have
S = |Ms| = ms1 + ms2 + ms3 + ms4 + ms5 + ms6
= - + - + - =0
Thus, term is 1So. We will find this to be true for ANY filled
subshell. More interesting then to consider unfilled shells.

Atomic Term Symbols

What is the term symbol for helium with a 1s12s1
configuration?
L = 0 (why?)
S = + , - = 1, 0
Thus there are two possibilities: 3S and 1S

Atomic Term Symbols

Energy level diagram for helium then is

parahelium
1S
1P
1D

orthohelium
3S
3P
3D

Atomic Term Symbols

What about an atom with the configuration 1s2,2s2, 2p1,3p1
(corresponds to an excited state for carbon)

L = l1 + l 2 , l1 + l 2 1, l1 + l 2 2,...l1 l 2
L = 2, 1, 0

D, P, and S

S can have S = 1, 0
Given these values for L and S we have
3D, 1D, 3P, 1P, 3S,

and 1S

Atomic Term Symbols

Including total orbital angular momentum, we need to consider
the following
3D

3,

3D

2,

3D

1,

1D

2,

3P , 3P , 3P , 1P , 3S ,
2
1
0
1
1

and 1So

Question is, which of these terms corresponds to the lowest

energy state??
Use Hunds Rules to determine!

Atomic Term Symbols

Hunds Rules
1. State with the largest value of S is most stable and stability
decreases with decreasing S.
2. For states with same values of S, the state with the largest
value of L is the most stable.
3. If states have same values of L and S then, for a subshell
that is less than half filled, state with smallest J is most
stable; for subshells that are more than half filled, state with
largest value of J is most stable.

Atomic Term Symbols

Here we are considering the terms 3D, 3P, 3S, 1D, 1P, 1S. In
terms of stability we can rank these terms as
1S
1P
1D
3S
3P
3D

Most stable

Given that the 3D states are most stable, which of these terms
correspond to the most stable state?

Atomic Term Symbols

Since the two p subshells are less than half filled, we would
predict that the 3D1 term corresponds to the most stable
state!
Simple approach for finding the ground state term symbol for
any atom:
1. Find maximum value of S consistent with the Pauli
Exclusion Principle S = Smax.
2. For S = Smax, find the maximum value of L consistent with
the Pauli Exclusion Principle L = Lmax.
3. Apply Hunds Rules to find J for most stable state.