Ch5 Rational Choice

Chapter Five
Choice
Economic Rationality
The principal behavioral postulate is
that a decisionmaker chooses its
most preferred alternative from those
available to it.
The available choices constitute the
choice set.
How is the most preferred bundle in
the choice set located?
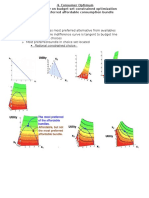
Rational Constrained Choice
x
1
x
2
x
1
x
2
Utility
Utility
x
2
x
1
x
1
x
2
Utility
Utility
x
1
x
2
Utility
x
1
x
2
Utility
x
1
x
2
Utility
x
1
x
2
Utility
x
1
x
2
Affordable, but not
the most preferred
affordable bundle.
x
1
x
2
Utility
Affordable, but not
the most preferred
affordable bundle.
The most preferred
of the affordable
bundles.
x
1
x
2
Utility
Utility
x
1
x
2
Utility
x
1
x
2
Utility
x
1
x
2
x
1
x
2
x
1
x
2
Affordable
bundles
x
1
x
2
Affordable
bundles
x
1
x
2
Affordable
bundles
More preferred
bundles
Affordable
bundles
x
1
x
2
More preferred
bundles
x
1
x
2
x
1
*
x
2
*
x
1
x
2
x
1
*
x
2
*
(x
1
*,x
2
*) is the most
preferred affordable
bundle.
The most preferred affordable bundle
is called the consumers ORDINARY
DEMAND at the given prices and
budget.
Ordinary demands will be denoted by
x
1
*(p
1
,p
2
,m) and x
2
*(p
1
,p
2
,m).
When x
1
* > 0 and x
2
* > 0 the
demanded bundle is INTERIOR.
If buying (x
1
*,x
2
*) costs $m then the
budget is exhausted.
x
1
x
2
x
1
*
x
2
*
(x
1
*,x
2
*) is interior.
(x
1
*,x
2
*) exhausts the
budget.
x
1
x
2
x
1
*
x
2
*
(x
1
*,x
2
*) is interior.
(a) (x
1
*,x
2
*) exhausts the
budget; p
1
x
1
* + p
2
x
2
* = m.
x
1
x
2
x
1
*
x
2
*
(x
1
*,x
2
*) is interior .
(b) The slope of the indiff.
curve at (x
1
*,x
2
*) equals
the slope of the budget
constraint.
(x
1
*,x
2
*) satisfies two conditions:
(a) the budget is exhausted;
p
1
x
1
* + p
2
x
2
* = m
(b) the slope of the budget constraint,
-p
1
/p
2
, and the slope of the
indifference curve containing (x
1
*,x
2
*)
are equal at (x
1
*,x
2
*).
Computing Ordinary Demands
How can this information be used to
locate (x
1
*,x
2
*) for given p
1
, p
2
and
m?
Computing Ordinary Demands -
a Cobb-Douglas Example.
Suppose that the consumer has
Cobb-Douglas preferences.
U x x x x
a b
( , )
1 2 1 2
=
Suppose that the consumer has
Cobb-Douglas preferences.

Then
U x x x x
a b
( , )
1 2 1 2
=
MU
U
x
ax x
a b
1
1
1
1
2
= =

c
c
MU
U
x
bx x
a b
2
2
1 2
1
= =

c
c
So the MRS is
MRS
dx
dx
U x
U x
ax x
bx x
ax
bx
a b
a b
= = = =
2
1
1
2
1
1
2
1 2
1
2
1
c c
c c
/
/
.
So the MRS is

At (x
1
*,x
2
*), MRS = -p
1
/p
2
so
MRS
dx
dx
U x
U x
ax x
bx x
ax
bx
a b
a b
= = = =
2
1
1
2
1
1
2
1 2
1
2
1
c c
c c
/
/
.
So the MRS is

At (x
1
*,x
2
*), MRS = -p
1
/p
2
so
MRS
dx
dx
U x
U x
ax x
bx x
ax
bx
a b
a b
= = = =
2
1
1
2
1
1
2
1 2
1
2
1
c c
c c
/
/
.
= =
ax
bx
p
p
x
bp
ap
x
2
1
1
2
2
1
2
1
*
*
* *
.
(A)
(x
1
*,x
2
*) also exhausts the budget so
p x p x m
1 1 2 2
* *
. + =
(B)
So now we know that
x
bp
ap
x
2
1
2
1
* *
=
(A)
p x p x m
1 1 2 2
* *
. + =
(B)
So now we know that
x
bp
ap
x
2
1
2
1
* *
=
(A)
p x p x m
1 1 2 2
* *
. + =
(B)
Substitute
So now we know that
x
bp
ap
x
2
1
2
1
* *
=
(A)
p x p x m
1 1 2 2
* *
. + =
(B)
p x p
bp
ap
x m
1 1 2
1
2
1
* *
. + =
Substitute
and get
This simplifies to .
x
am
a b p
1
1
*
( )
. =
+
x
bm
a b p
2
2
*
( )
. =
+
Substituting for x
1
* in
p x p x m
1 1 2 2
* *
+ =
then gives
x
am
a b p
1
1
*
( )
. =
+
So we have discovered that the most
preferred affordable bundle for a consumer
with Cobb-Douglas preferences

U x x x x
a b
( , )
1 2 1 2
=
is
( , )
( )
,
( )
.
* *
( ) x x
am
a b p
bm
a b p
1 2
1 2
=
+ +
x
1
x
2
x
am
a b p
1
1
*
( )
=
+
x
bm
a b p
2
2
*
( )
=
+
U x x x x
a b
( , )
1 2 1 2
=
When x
1
* > 0 and x
2
* > 0
and (x
1
*,x
2
*) exhausts the budget,
and indifference curves have no
kinks, the ordinary demands are
obtained by solving:
(a) p
1
x
1
* + p
2
x
2
* = y
(b) the slopes of the budget constraint,
-p
1
/p
2
, and of the indifference curve
containing (x
1
*,x
2
*) are equal at (x
1
*,x
2
*).
But what if x
1
* = 0?
Or if x
2
* = 0?
If either x
1
* = 0 or x
2
* = 0 then the
ordinary demand (x
1
*,x
2
*) is at a
corner solution to the problem of
maximizing utility subject to a budget
constraint.
Examples of Corner Solutions --
the Perfect Substitutes Case
x
1
x
2
MRS = -1
x
1
x
2
MRS = -1
Slope = -p
1
/p
2
with p
1
> p
2
.
x
1
x
2
MRS = -1
Slope = -p
1
/p
2
with p
1
> p
2
.
x
1
x
2
x
y
p
2
2
*
=
x
1
0
*
=
MRS = -1
Slope = -p
1
/p
2
with p
1
> p
2
.
x
1
x
2
x
y
p
1
1
*
=
x
2
0
*
=
MRS = -1
Slope = -p
1
/p
2
with p
1
< p
2
.
So when U(x
1
,x
2
) = x
1
+ x
2
, the most
preferred affordable bundle is (x
1
*,x
2
*)
where
|
.
|
\
|
= 0 ,
p
y
) x , x (
1
*
2
*
1
and
|
.
|
\
|
=
2
*
2
*
1
p
y
, 0 ) x , x (
if p
1
< p
2

if p
1
> p
2
.
x
1
x
2
MRS = -1
Slope = -p
1
/p
2
with p
1
= p
2
.
y
p
1
y
p
2
x
1
x
2
All the bundles in the
constraint are equally the
most preferred affordable
when p
1
= p
2
.
y
p
2
y
p
1
the Non-Convex Preferences Case
x
1
x
2
x
1
x
2
x
1
x
2
Which is the most preferred
affordable bundle?
x
1
x
2
The most preferred
affordable bundle
x
1
x
2
The most preferred
affordable bundle
Notice that the tangency solution
is not the most preferred affordable
bundle.
Examples of Kinky Solutions --
the Perfect Complements Case
x
1
x
2
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
x
1
x
2
MRS = 0
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
x
1
x
2
MRS = -
MRS = 0
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
x
1
x
2
MRS = -
MRS = 0
MRS is undefined
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
x
1
x
2
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
x
1
x
2
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
Which is the most
preferred affordable bundle?
x
1
x
2
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
The most preferred
affordable bundle
x
1
x
2
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
x
1
*
x
2
*
x
1
x
2
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
x
1
*
x
2
*
(a) p
1
x
1
* + p
2
x
2
* = m
x
1
x
2
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
x
1
*
x
2
*
(a) p
1
x
1
* + p
2
x
2
* = m
(b) x
2
* = ax
1
*
(a) p
1
x
1
* + p
2
x
2
* = m; (b) x
2
* = ax
1
*.
(a) p
1
x
1
* + p
2
x
2
* = m; (b) x
2
* = ax
1
*.
Substitution from (b) for x
2
* in
(a) gives p
1
x
1
* + p
2
ax
1
* = m
(a) p
1
x
1
* + p
2
x
2
* = m; (b) x
2
* = ax
1
*.
2
* in
(a) gives p
1
x
1
* + p
2
ax
1
* = m
which gives
2 1
*
1
ap p
m
x
+
=
(a) p
1
x
1
* + p
2
x
2
* = m; (b) x
2
* = ax
1
*.
2
* in
(a) gives p
1
x
1
* + p
2
ax
1
* = m
which gives
.
ap p
am
x ;
ap p
m
x
2 1
*
2
2 1
*
1
+
=
+
=
(a) p
1
x
1
* + p
2
x
2
* = m; (b) x
2
* = ax
1
*.
2
* in
(a) gives p
1
x
1
* + p
2
ax
1
* = m
which gives
A bundle of 1 commodity 1 unit and
a commodity 2 units costs p
1
+ ap
2
;
m/(p
1
+ ap
2
) such bundles are affordable.
.
ap p
am
x ;
ap p
m
x
2 1
*
2
2 1
*
1
+
=
+
=
x
1
x
2
U(x
1
,x
2
) = min{ax
1
,x
2
}
x
2
= ax
1
x
m
p ap
1
1 2
*
=
+
x
am
p ap
2
1 2
*
=
+

Ch5 Rational Choice

Uploaded by

Document Information

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Ch5 Rational Choice

Uploaded by

Copyright:

Available Formats

Chapter Five

You might also like