Applications of Definite Integrals

Advanced Level Pure Mathematics

Advanced Level Pure Mathematics

Applications of Definite Integrals

Areas

Arc Length

Volumes of Solids of Revolution

11

Area of Surface of Revolution

13

Prepared by Mr. K.

Page 1

F. Ngai

Applications of Definite Integrals

Advanced Level Pure Mathematics

Areas
A

Equations of Curves are represented in Rectangular Form

Let A denote the area ( or total area) of the shaded region.

Theorem

The area enclosed by the graph of y = f (x) , the x-axis and the lines x = a and x = b is
equal to

Theorem

f (x) dx or

y dx.

The area enclosed by the graph of x = g(y) , the x-axis and the lines y = c and y = d is
equal to

g(y) dy or

x dy.

Prepared by Mr. K.

Page 2

F. Ngai

Applications of Definite Integrals

Example

Advanced Level Pure Mathematics

Find the area enclosed by the graph of y = x , the axis and the lines x = 1 and x = 3 .
2

Solution

Example

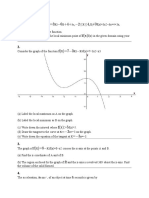
Find the area bounded by the following curves.

x2 y2
+
= 1.
a2 b2

(a)

Ellipse:

(b)

x = a(t sint)
Cycloid:
, 0 t 2 and x-axis.
y = a(1 cost)

Prepared by Mr. K.

Page 3

F. Ngai

Applications of Definite Integrals

Example

Advanced Level Pure Mathematics

Find the area enclosed by the graph y = x + 1 , the y-axis and the lines y = 2 and y = 3 .

Example

Given a conic C : x2 + 4y2 6x + 8y + 9 = 0.

(a)
(b)

By completing squares and translation coordinate axes, transform the equation of

C to standard form. What is this curve?
find the area of the region bounded by C .
( Ans: 2 )

Solution

Prepared by Mr. K.

Page 4

F. Ngai

Applications of Definite Integrals

Advanced Level Pure Mathematics

B

Equations of Curves are in parametric Form

It is known that the area between the curve y = f (x) and the lines x = a , x = b and y = 0
is given by

y dx.

x = F(t)
If the equation of the curve is in parametric form
,
y = G(t)

where t is a parameter, and if

t =
t =

when x = a;
when x = b,

dx
= F' (t) is a continuous function on [,], and F' (t) does not change sign is in (, ),
dt
x = F(t)
then the area of the region bounded by the curve
, the x-axis and the lines
y = G(t)

x = a , x = b is

G(t) F' (t)dt= y x' (t)dt. ( Integration by substitution )

This formula is also true when if > . In this case

dx
= F' (t) 0 for all t (, ) .
dt

Example

x = acost
Find the area of the ellipse
, where a > 0, b > 0.
y = b sint

Example

x = t2 2
Consider the curve
. Find the area bounded by the curve and y-axis.
2t
y =

Prepared by Mr. K.

Page 5

F. Ngai

Applications of Definite Integrals

Advanced Level Pure Mathematics

AL91II-3

x = sin3 t

Consider the curve

, 0 t .
3
2
y = cos t
Find the area bounded by the curve, the x-axis and y-axis.

Solution

The figure is symmetric about both of the coordinates axes.

Example

x = t2 1
. Find the area bounded by Loop of curve.
Consider the curve
3
y = t t

Prepared by Mr. K.

Page 6

F. Ngai

Applications of Definite Integrals

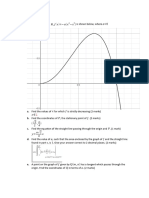
Example

Advanced Level Pure Mathematics

Suppose that the curve in figure with parametric form x = f (t) , y = g(t) . If t1 and t2 are
the parameters of points A and B . Show the shaded area is

1 t2 dy dx
(x y )dt.
2 t1 dt
dt

Prepared by Mr. K.

Page 7

F. Ngai

Applications of Definite Integrals

Advanced Level Pure Mathematics

Arc Lengths
A

Equations of curves are in Rectangular Form

Theorem

If a curve y = f (x) has a continuous derivative on [a,b], then the length of the curve from

x = a to x = b is given by

Remark

1 + (f ' (x))2 dx =

dy
1 + dx.
dx

If the equation of the curve is in the form x = g(y) , then the length of the arc between y = c
2

and y = d is given by

1 + (g ' (x)) dy=

dx
1 + dy.
dy

Example

Find the length of the parabolic arc y2 = 4x from (0,0) to (4,4) .

Example

Find the length of the loop of the curve 12y2 = x(4 x)2 .

Remark

Prepared by Mr. K.

Page 8

F. Ngai

Applications of Definite Integrals

Advanced Level Pure Mathematics

B

Equations of Curves are in Parametric Form

Theorem

When a function is expressed in parametric form x = f (t) and y = g(t) , the arc length s of
the curve from t = a to t = b is given by

s=

(f ' (t))2 + (g' (t))2 dt

Example

Find the length of curve x = 4t2 , y = 2t3 between t = 0, t = 1 .

Example

Find the length of the loop of the curve 9ay2 = x(3a x)2 , a > 0.

Prepared by Mr. K.

Page 9

F. Ngai

Applications of Definite Integrals

Advanced Level Pure Mathematics

AL91II-3

x = sin3 t

Consider the curve

, 0 t .
3
2
y = cos t
Find the length of the curve.

Example

x = acos3 t
where a > 0.
Find the total length of the curve:
3
y = asin t,

Question

In the above example, as t increases from 0 to 2 , the point will move along the curve for a
complete turn. Is it correct to find the arc length by evaluating the integral

sin2 t
dx dy
+ dt= 3a
?
dt dt
2 0
2

Always bear in mind that

dx dy
+ 0.
dt dt

Prepared by Mr. K.

Page 10

F. Ngai

Applications of Definite Integrals

Advanced Level Pure Mathematics

Volumes of Solids of Revolution

A

Disc Method

Theorem

Let y = f (x) be a continuous function defined on [a, b], and S be the region bounded by
the curve y = f (x) , the lines x = a , x = b and the x-axis. Then the volume V of the solid
generated by revolving the region S one complete revolution about the x-axis is given by
b

V = y2dx = [f (x)] dx.

Remark

x = h(t)
, the volume of solid of resolution generated by revolving the
In parametric form
y = g(t)

region enclosed by the graph, x-axis and from t1 to t2 about x-axis.

t2

V = (g(t))2h' (t)dt
t1

Theorem

Let y = f (x) be a continuous function defined on [a, b], and S be the region bounded by
the curve y = f (x) , the lines x = a , x = b and y = h . Then the volume V of the solid
generated by revolving the region S one complete revolution about the y = h is given by
b

V = (y h)2 dx = [f (x) h] dx
Example

Find the volume of the solid generated by revolving one complete revolution of the upper half
2

x y 3
region of the closed curve + = 1 about the line y = b , (a > 0,b > 0) .
a b

Prepared by Mr. K.

Page 11

F. Ngai

Applications of Definite Integrals

Example

Advanced Level Pure Mathematics

Find the volume of the solid generated by revolving the region bounded by the cycloid
x = a(t sint), y = a(1 cost), where a > 0 and 0 t 2 , and the x-axis about the
x-axis.

Example

Find the volume of solid generated by revolving the region bounded by the curve x = cos3 t
y = sin3 t about y-axis.

Shell Method

Theorem

Let f be a function continuous on [a, b]. If the area bounded by the graph of f (x) , the
x-axis and the lines x = a and x = b is revolved about the y-axis, the volume V of solid
generated is

Example

2 xf(x)dx

Derive a formula for evaluation the volume of a cylinder of a radius a and height h by using
the shell method.

Prepared by Mr. K.

Page 12

F. Ngai

Applications of Definite Integrals

Example

Advanced Level Pure Mathematics

Find the volume of the solid generated by revolving the region bounded by the curves
2

y = x2 + x , y = e x and the lines x = 1, x = 2 one complete revolution about the y-axis.

Area of Surface of Revolution

Theorem

Suppose y = f (x) has a continuous derivative on [a, b]. Then the area S of the surface of
revolution by the arc of the curve y = f (x) between x = a and x = b about the x-axis is
S

Remark

2 f (x) 1 + [f ' (x)] 2 dx

a

dy
y 1 + dx
dx

The corresponding formula for the area of the surface of revolution obtained by revolving an
arc of a curve x = g(y) from y = c to y = d about the y-axis is
S

2 g(y) 1 + [g' (y)] 2 dy

c

Theorem

dx
x 1 + dy
dy

If a portion of the curve of parametric equations x = x(t) , y = y(t) between the points
corresponding to t1 and t2 is revolved about the x-axis, the surface area S is
S

t2

t2

t1

t1

2 y(t)ds= 2 y(t) [x' (t)]2 + [y' (t)]2 dt.

Prepared by Mr. K.

Page 13

F. Ngai

Applications of Definite Integrals

Advanced Level Pure Mathematics

Example

x = r cos
Consider the curve
. Find the surface area of a sphere.
y = r sin

AL93II-4

Find the area of the surface obtained by rotating the following curve about the x-axis:

x = sin3 t
,

3
y = cos t

Example

t .
2
2

Find the area of the surface generated by rotating the arc of the curve x = et sint ,
y = et cost, from t = 0 to t =

about the x-axis.

2

Prepared by Mr. K.

Page 14

F. Ngai

Applications of Definite Integrals

Example

Advanced Level Pure Mathematics

Find the area of surface generated by revolving the graph of x = 3t2 , y = t3 between t = 0
and t = 2 about y-axis.

Example

The curve C is represented by x = 4t2 and y = t4 4lnt

(a)

Find the length of the loop of C from t = 1 to t = 2 .

(b)

Find the Volume of the solid generated by revolving the arc in (a) about y-axis. Find
also the surface area.

Prepared by Mr. K.

Page 15

F. Ngai