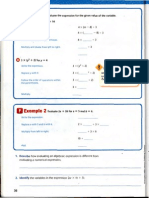
Chapter 4(A)

IB Math Studies I

[ notes ]

4A: Algebraic Substitution

The difference between an Expression & Equation.
Expression
Equation
3x + 2
2x + 3 = 15
Made up of terms
Cannot be solved,
we must know a
value to substitute
into the variable.

Made up of terms
Can be solved with
algebraic steps to
isolate the variable.
We undo by using
inverse operations.

Substitution is the process of evaluating an

expression by placing input values into
designated variables.
Examples:

1. If p=-2, evaluate: -3( p - 4 )

answer: 18

2. If m=-2 & g=4, find:

answer: -3

Chapter 4(B)

IB Math Studies I

[ notes ]
4A: Algebraic Substitution

When the expressions become more

complex we need to follow the orders of
operations (left to right)!
Simplifying Expressions

IMPORTANT: This DOES NOT mean Multiply

before Divide or Add before Subtract. It means if
they are side-by-side they must be performed
left to right!
Examples:

3. If p=-4 & m=2, evaluate: (4p pm)3

answer: 512

Chapter 4(B)

IB Math Studies I

[ notes ]

4B: Linear Equations

The Linear Equation: ax + b = 0.
x is the variable or unknown.
a & b are constants.
4A: Algebraic Substitution

When the expressions become more

complex we need to follow the orders of
operations (left to right)!

IMPORTANT: We must do the inverse

operations to solve. This means performing the
order of operations in reverse (inverse).
Examples you will need to know how to solve:
1.

4.

2.

5.

3.
answers:

1. x = 9

2. x =

3. x = 3

4. x = -2

5. x =