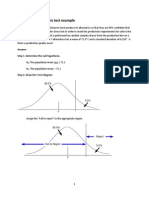
Steps

to Solve a ChiSquare Test problem

1) Determine the null hypothesis and alternate hypothesis
*Null (H0): two variables are independent
Alternate (H1): two variables are not independent

2) Calculate the Expected Value matrix
*Exp. Value = (row total)(column total)/sample size
*The expected value of each cell must be 5 or greater for
ChiSquare test to be valid

3) Determine the Chi-Square statistic for the data
2 (Observed Expected)2
* = Expected

4) Find the Degrees of Freedom
* D.F. = (rows 1)(columns 1)

5) Compare the Chi-Square statistic (your calculated value) to
the critical value at the appropriate level of significance (the
value from the chart in the book in the table on p. A26)
(default value is .050)

6) If Chi-Square statistic < critical value,
accept the Null hypothesis
(variables are independent)
If Chi-Square statistic > critical value,
reject the Null hypothesis and accept the alternate hypothesis
(variables are not independent)