Professional Documents
Culture Documents
Automorphism Group of A Cyclic Group: References
Automorphism Group of A Cyclic Group: References
Uploaded by
bacilul0 ratings0% found this document useful (0 votes)
10 views1 pageThe automorphism group of a cyclic group Z/nZ is the multiplicative group (Z/nZ)×, which has order φ(n), where φ is the Euler totient function. A proof shows that every element a relatively prime to n induces an automorphism by sending the generator x to x^a. This defines an isomorphism from the automorphism group to (Z/nZ)×.
Original Description:
Matematica
Original Title
41475
Copyright
© © All Rights Reserved
Available Formats
PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentThe automorphism group of a cyclic group Z/nZ is the multiplicative group (Z/nZ)×, which has order φ(n), where φ is the Euler totient function. A proof shows that every element a relatively prime to n induces an automorphism by sending the generator x to x^a. This defines an isomorphism from the automorphism group to (Z/nZ)×.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
0 ratings0% found this document useful (0 votes)
10 views1 pageAutomorphism Group of A Cyclic Group: References
Automorphism Group of A Cyclic Group: References
Uploaded by
bacilulThe automorphism group of a cyclic group Z/nZ is the multiplicative group (Z/nZ)×, which has order φ(n), where φ is the Euler totient function. A proof shows that every element a relatively prime to n induces an automorphism by sending the generator x to x^a. This defines an isomorphism from the automorphism group to (Z/nZ)×.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
You are on page 1of 1
automorphism group of a cyclic group
rm50
2013-03-22 2:23:07
Theorem 1. The automorphism group of the cyclic group Z/nZ is (Z/nZ) ,
which is of order (n) (here is the Euler totient function).
Proof. Choose a generator x for Z/nZ. If Aut(Z/nZ), then (x) = xa for
some integer a (defined up to multiples of n); further, since x generates Z/nZ,
it is clear that a uniquely determines . Write a for this automorphism. Since
a is an automorphism, xa is also a generator, and thus a and n are relatively
prime1 . Clearly, then, every a relatively prime to n induces an automorphism.
We can therefore define a surjective map
: Aut(Z/nZ) (Z/nZ) : a 7 a (mod n)
is also obviously injective, so all that remains is to show that it is a group
homomorphism. But for every a, b (Z/nZ) , we have
(a b )(x) = a (xb ) = (xb )a = xab = ab (x)
and thus
(a b ) = (ab ) = ab (mod n) = (a )(b )
References
[1] Dummit, D., Foote, R.M., Abstract Algebra, Third Edition, Wiley, 2004.
hAutomorphismGroupOfACyclicGroupi created: h2013-03-2i by: hrm50i version:
h41475i Privacy setting: h1i hTheoremi h20A05i h20F28i
This text is available under the Creative Commons Attribution/Share-Alike License 3.0.
You can reuse this document or portions thereof only if you do so under terms that are
compatible with the CC-BY-SA license.
1 If they were not, say (a, n) = d, then (xa )n/d = (xa/d )n = 1 so that xa would not
generate.
You might also like
- Homework #2, Sec 10.2Document5 pagesHomework #2, Sec 10.2Masaya Sato91% (11)
- DanishDocument34 pagesDanishzakaurrehman333100% (1)
- Unit 10 AssignmentDocument36 pagesUnit 10 Assignmentvatanemp 000100% (2)
- Tsogtgerel GantumurDocument7 pagesTsogtgerel GantumurverbicarNo ratings yet
- Assignment 4Document1 pageAssignment 4Harsh SanklechaNo ratings yet
- Homomorphisms From R/ (R) To R/(S) For A Principal Ideal Domain RDocument7 pagesHomomorphisms From R/ (R) To R/(S) For A Principal Ideal Domain RMétodos NuméricosNo ratings yet
- Units Modulo A PrimeDocument3 pagesUnits Modulo A PrimeAmiya BiswasNo ratings yet
- Math 121 Homework 1: Notes On Selected ProblemsDocument9 pagesMath 121 Homework 1: Notes On Selected ProblemsLuisVillotaNo ratings yet
- 542hw5 SolnsDocument5 pages542hw5 SolnsSoumen GhoshNo ratings yet
- Jensen Script August 03 2016Document145 pagesJensen Script August 03 2016BRAHYAN ALBERTO ROJAS ALBARRACINNo ratings yet
- Myhill-Nerode Theorem: able by A iff for every string z ∈ ΣDocument2 pagesMyhill-Nerode Theorem: able by A iff for every string z ∈ ΣKushal KanungoNo ratings yet
- MCMC: Metropolis Hastings AlgorithmDocument5 pagesMCMC: Metropolis Hastings AlgorithmTamás MákosNo ratings yet
- Number Theory 2Document8 pagesNumber Theory 2Soumabha NandiNo ratings yet
- Optional:: Date: January 24, 2024Document1 pageOptional:: Date: January 24, 2024VIKAS KUMARNo ratings yet
- Ring Homomorphisms: DefinitionDocument4 pagesRing Homomorphisms: DefinitionTom DavisNo ratings yet
- P3Homomorph PDFDocument25 pagesP3Homomorph PDFJeoff Libo-onNo ratings yet
- SIUE 2008 Fall Math 320 Chapter 15 Study GuideDocument3 pagesSIUE 2008 Fall Math 320 Chapter 15 Study GuideNathaniel R. ReindlNo ratings yet
- R, Fuzzy R, and Algebraic Kripke-Style: SemanticsDocument16 pagesR, Fuzzy R, and Algebraic Kripke-Style: SemanticsQfwfq RedipiccheNo ratings yet
- Solution Outlines For Chapter 10Document4 pagesSolution Outlines For Chapter 10Dawna AkonaNo ratings yet
- Homework Solution 11Document4 pagesHomework Solution 11michael turksonNo ratings yet
- Homomorphisms of Groups 3Document65 pagesHomomorphisms of Groups 3JAHANZAIBNo ratings yet
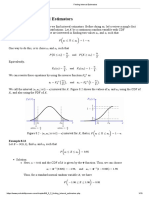
- Finding Interval EstimatorsDocument13 pagesFinding Interval EstimatorsbossishereNo ratings yet
- Riemann MappingDocument7 pagesRiemann MappingDitmar Sayritupac VenturaNo ratings yet
- The (, Q) - Fuzzy Subsemigroups and Ideals of An (, Q) - Fuzzy SemigroupDocument10 pagesThe (, Q) - Fuzzy Subsemigroups and Ideals of An (, Q) - Fuzzy Semigrouppri911No ratings yet
- A Proof of Arrow's Impossibility TheoremDocument3 pagesA Proof of Arrow's Impossibility TheoremLavanya YadavNo ratings yet
- Industrial Mathematics Institute: Research ReportDocument25 pagesIndustrial Mathematics Institute: Research ReportpostscriptNo ratings yet
- Complex Analysis Exercise Sheet Nb. 6: V. Féray April 10th, 2018Document2 pagesComplex Analysis Exercise Sheet Nb. 6: V. Féray April 10th, 2018Anonymous NvXx5OP4wCNo ratings yet
- Lecture Notes 2022Document47 pagesLecture Notes 2022Scribd UserNo ratings yet
- 1 Complex Theory of Abelian Varieties: X X X K KDocument16 pages1 Complex Theory of Abelian Varieties: X X X K KvahidNo ratings yet
- MIT18 905F16 Lec10Document5 pagesMIT18 905F16 Lec10Arindam BandyopadhyayNo ratings yet
- NotesDocument21 pagesNotesGiannis KordonisNo ratings yet
- Cs229-Notes8 em Algo 2019Document14 pagesCs229-Notes8 em Algo 2019bobNo ratings yet
- Convergence of NetsDocument12 pagesConvergence of NetsANDRES DAVID GUEVARA MENDOZANo ratings yet
- SobolevDocument35 pagesSobolevFrancisco PiresNo ratings yet
- App Group OidsDocument26 pagesApp Group OidsSixta VivancoNo ratings yet
- Logic Problem Set 3: Michael Lin 17 October 2016Document1 pageLogic Problem Set 3: Michael Lin 17 October 2016michaellin1767No ratings yet
- Formal Differential Equations and Renormalization: FR Ed Eric MenousDocument18 pagesFormal Differential Equations and Renormalization: FR Ed Eric MenouspedroNo ratings yet
- Algebraic Eigenvalue Problem Algebraic Eigenvalue Problem: Fall 2010Document76 pagesAlgebraic Eigenvalue Problem Algebraic Eigenvalue Problem: Fall 2010JonyQuispeNo ratings yet
- Symmetries of WDVV 38Document12 pagesSymmetries of WDVV 38Huong Cam ThuyNo ratings yet
- Deciding The Status of Arguments in Abstract Argumentation Frameworks: Tableaux With Boolean OperationsDocument11 pagesDeciding The Status of Arguments in Abstract Argumentation Frameworks: Tableaux With Boolean OperationsMarcelo AudayNo ratings yet
- HW 10 SolnDocument1 pageHW 10 SolnVaibhavi MauryaNo ratings yet
- Homo Morphis M NewDocument24 pagesHomo Morphis M NewErica CanonNo ratings yet
- MEE211-Distributed LoadsDocument14 pagesMEE211-Distributed Loadsigverified56No ratings yet
- Fuzzy SetDocument13 pagesFuzzy SetSoumya PaikNo ratings yet
- Normal Subgroups and Quotient Groups: 4.1 Group HomomorphismsDocument3 pagesNormal Subgroups and Quotient Groups: 4.1 Group HomomorphismsMarlydTalakuaNo ratings yet
- Soal Homomorfisma PDFDocument5 pagesSoal Homomorfisma PDFShandy NugrahaNo ratings yet
- Math MSC NotesDocument16 pagesMath MSC NotesPatricia SuratnoNo ratings yet
- HomomorphismlectureDocument4 pagesHomomorphismlectureErica CanonNo ratings yet
- Paul C. Eklof and Saharon Shelah - New Non-Free Whitehead Groups (Corrected Version)Document5 pagesPaul C. Eklof and Saharon Shelah - New Non-Free Whitehead Groups (Corrected Version)Jgfm2No ratings yet
- Robin Zhang: n+1 (R) (S) (R) (S) N I 1 I I N I 1 I IDocument8 pagesRobin Zhang: n+1 (R) (S) (R) (S) N I 1 I I N I 1 I IArooj RazaNo ratings yet
- 5.semi Comp OpDocument24 pages5.semi Comp OpCristhian AvilaNo ratings yet
- CrraoDocument7 pagesCrraoSouparna MukhopadhyayNo ratings yet
- ThermodynamicsDocument10 pagesThermodynamicsabhishekNo ratings yet
- Proof of The Riemann Mapping TheoremDocument3 pagesProof of The Riemann Mapping TheoremTendai M Mudziiri ShumbaNo ratings yet
- WOMPtalk ManifoldsDocument11 pagesWOMPtalk ManifoldsKirk BennettNo ratings yet
- 2010 10 01 Lect2Document4 pages2010 10 01 Lect2johnkevinveraces847No ratings yet
- CorrespondencesDocument15 pagesCorrespondencesSamy YNo ratings yet
- Finding Interval EstimatorsDocument10 pagesFinding Interval EstimatorsSahas ParabNo ratings yet
- Discrete Series of GLn Over a Finite Field. (AM-81), Volume 81From EverandDiscrete Series of GLn Over a Finite Field. (AM-81), Volume 81No ratings yet