Professional Documents
Culture Documents
Electronic Devices and Integrated Circuits (El2006) : Lecture 2 (21 September, 2010)
Electronic Devices and Integrated Circuits (El2006) : Lecture 2 (21 September, 2010)
Uploaded by
Shivam Luthra0 ratings0% found this document useful (0 votes)
20 views23 pages1) The lecture discussed semiconductor wafers, energy bands in semiconductors, and charge carriers.
2) Key distinctions between direct and indirect bandgap semiconductors were explained, such as GaAs being a direct bandgap semiconductor.
3) It was noted that around 1.5 x 1010 electron-hole pairs exist per cm3 of silicon at room temperature, but there are only around 3 pairs per 1013 silicon atoms, showing it is a small fraction.
Original Description:
Original Title
3930.EDIC LECTURE 2 210910
Copyright
© Attribution Non-Commercial (BY-NC)
Available Formats
PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this Document1) The lecture discussed semiconductor wafers, energy bands in semiconductors, and charge carriers.
2) Key distinctions between direct and indirect bandgap semiconductors were explained, such as GaAs being a direct bandgap semiconductor.
3) It was noted that around 1.5 x 1010 electron-hole pairs exist per cm3 of silicon at room temperature, but there are only around 3 pairs per 1013 silicon atoms, showing it is a small fraction.
Copyright:
Attribution Non-Commercial (BY-NC)
Available Formats
Download as PDF, TXT or read online from Scribd
0 ratings0% found this document useful (0 votes)
20 views23 pagesElectronic Devices and Integrated Circuits (El2006) : Lecture 2 (21 September, 2010)
Electronic Devices and Integrated Circuits (El2006) : Lecture 2 (21 September, 2010)
Uploaded by
Shivam Luthra1) The lecture discussed semiconductor wafers, energy bands in semiconductors, and charge carriers.
2) Key distinctions between direct and indirect bandgap semiconductors were explained, such as GaAs being a direct bandgap semiconductor.
3) It was noted that around 1.5 x 1010 electron-hole pairs exist per cm3 of silicon at room temperature, but there are only around 3 pairs per 1013 silicon atoms, showing it is a small fraction.
Copyright:
Attribution Non-Commercial (BY-NC)
Available Formats
Download as PDF, TXT or read online from Scribd
You are on page 1of 23
ELECTRONIC DEVICES AND
INTEGRATED CIRCUITS (EL2006)
LECTURE 2 (21st September, 2010)
EL2006 Rajnish Sharma, Chitkara 1
University
Last Class
Need of learning EDIC !
Detailed discussion on organization of course
handout
Golden rule for research in Electronics
EL2006 Rajnish Sharma, Chitkara 2
University
Today’s class
You will
Get to see a silicon wafer and appreciate
few facts
Learn origin of energy bands
Learn about distinction between Direct
and indirect bandgap SCs
Charge Carriers in SCs
EL2006 Rajnish Sharma, Chitkara 3
University
Have a careful look at silicon wafer !
Observe some facts
* One side of the wafer is polished, while
the other is rough
** It is important to ensure the ultra
smoothness of that side of the wafer, on
which you finally intend to fabricate
integrated circuits.
***<100> orientation is the most preferred
one, so as to make the devices.
EL2006 Rajnish Sharma, Chitkara 4
University
Distinction between Metals, semiconductors and
insulators
EL2006 Rajnish Sharma, Chitkara 5
University
Origin of Energy Bands
As isolated atoms are brought together to form a solid,
various interactions occur between neighboring atoms.
So, what should be there along X – axis on
energy band diagram ??
Inter atomic distance Correct
Let us make it more formalize
EL2006 Rajnish Sharma, Chitkara 6
University
We talk of E – K Diagram , where K
stands for wave vector !!
Question arises : What is ‘K’ ??
EL2006 Rajnish Sharma, Chitkara 7
University
K is basically the propagation constant of
the plane wave moving for example in the x
– direction. This plane wave is nothing, but
just the wave function of the electron.
Remind urself the concept of
Schrodinger’s wave equation!
EL2006 Rajnish Sharma, Chitkara 8
University
Wave function
A function appearing in Schrodinger’s eqn. in wave
mechanics. This is infact a mathematical
expresssion involving the coordinates of a particle in
space.
If the Schrodinger’s wave eqn. can be solved for a
particle in a given system ( e.g. an electron in an
atom ), then depending on the boundary conditions,
the solution is a set of allowed wave functions of the
particle each corresponding to an allowed energy
level.
EL2006 Rajnish Sharma, Chitkara 9
University
Space dependent wave function for the electron
Ψk(x) = U ( kx, x ) e jkxx
Where U ( kx, x) modulates the wave function according
to the periodicity of the lattice.
EL2006 Rajnish Sharma, Chitkara 10
University
K holds a relationship with momentum.
X – component of the electron momentum
in the crystal is given by
< px > = ħ kx
EL2006 Rajnish Sharma, Chitkara 11
University
Direct and Indirect bandgap Semiconductors :
EL2006 Rajnish Sharma, Chitkara 12
University
Direct Gap Semiconductor : Maximum of
the valence band and minimum of the
conduction band fall at the same place in k-
space. E.g. GaAs
## Can be used for making devices from
which we require light output.
EL2006 Rajnish Sharma, Chitkara 13
University
Indirect Gap Semiconductor: Maximum of
the valence band and minimum of the
conduction band fall different points in k-
space. e.g. Si
## Energy is generally given up as heat to
the lattice rather than as an emitted photon.
EL2006 Rajnish Sharma, Chitkara 14
University
Interesting !!!!!
Ga As P is a direct band gap semiconductor from
Ga As to about Ga As.55 P.45 and is indirect from
this composition to GaP.
Material is often used in visible LEDs.
EL2006 Rajnish Sharma, Chitkara 15
University
Why we have mentioned only GaAs
,why not Si????
EL2006 Rajnish Sharma, Chitkara 16
University
Problem
Calculate the photon energy corresponding to
a particular wavelength of 6000 Ao. (1Ao = 10-
10 mts. = 10-8 Cms)
EL2006 Rajnish Sharma, Chitkara 17
University
Charge Carriers in a Semiconductor
# In Semiconductors, due to a negotiable amount of
band gap, the conduction is of course dependent upon
temperature.
EL2006 Rajnish Sharma, Chitkara 18
University
# The promoted electron and the resulting hole
are referred to as an electron-hole pair.
# It is this movement of electrons which results in the
hole being termed as a second charge carrier. The hole
moves randomly through the material, but when an
external potential difference is applied the hole appears
to move from +ve to -ve at room temperature.
EL2006 Rajnish Sharma, Chitkara 19
University
How many electron hole pairs at room
temperature?
# 1.5 x 1010 electron-hole pairs in existence per
cm3 of silicon.
Sounds really a lot !!!!
# But, there are 5 x 1022 atoms of silicon per cm3,
so there are only approximately 3 electron-hole
pairs per 1013 atoms.
EL2006 Rajnish Sharma, Chitkara 20
University
Will any current flow ?
In case, when Valence band is completely filled or
Conduction band is completely empty ?
No !
EL2006 Rajnish Sharma, Chitkara 21
University
Next class :
# Charge carriers in semiconductors
(contd.)
# Effective mass
# Intrinsic and extrinsic semiconductors
EL2006 Rajnish Sharma, Chitkara 22
University
THANKS !
EL2006 Rajnish Sharma, Chitkara 23
University
You might also like
- Electrical Circuits and Circuit AnalysisDocument147 pagesElectrical Circuits and Circuit AnalysisGuruKPO100% (3)
- The Fallacy of Conductors and Proof of The Aether by Eric DollardDocument17 pagesThe Fallacy of Conductors and Proof of The Aether by Eric Dollardxreader0100% (2)
- ECEG 2131 AEI Lec 02 Carrier Transport and The PN Junction 2Document20 pagesECEG 2131 AEI Lec 02 Carrier Transport and The PN Junction 2yilkal EniyewNo ratings yet
- Silicon Crystal Grown by The Czochralski MethodDocument29 pagesSilicon Crystal Grown by The Czochralski MethodNeha PachauriNo ratings yet
- Solid-State Circuits: Electrical Engineering DivisonFrom EverandSolid-State Circuits: Electrical Engineering DivisonRating: 4.5 out of 5 stars4.5/5 (4)
- Modelling of Electric and Magnetic Fields Under HVAC Transmission Line - N. Yogambal & S.N. DeepaDocument9 pagesModelling of Electric and Magnetic Fields Under HVAC Transmission Line - N. Yogambal & S.N. DeepaCarlos NavarroNo ratings yet
- Ak Electronic Devices Unit 1Document8 pagesAk Electronic Devices Unit 1Shirin RazdanNo ratings yet
- Dr. Nasim Zafar: COMSATS Institute of Information Technology Virtual Campus IslamabadDocument43 pagesDr. Nasim Zafar: COMSATS Institute of Information Technology Virtual Campus IslamabadAhmerz Chillz WinterzNo ratings yet
- Material Science: Prof. Satish V. KailasDocument15 pagesMaterial Science: Prof. Satish V. KailasHagere EthiopiaNo ratings yet
- I Unit - Edc - MahiDocument26 pagesI Unit - Edc - Mahilucky jNo ratings yet
- E K Diagram Direct and Indirect Bandgap SemiconductorsDocument7 pagesE K Diagram Direct and Indirect Bandgap Semiconductorssupriya raiNo ratings yet
- Fundamentals of Energy Dispersive X-Ray Analysis: Butterworths Monographs in MaterialsFrom EverandFundamentals of Energy Dispersive X-Ray Analysis: Butterworths Monographs in MaterialsRating: 5 out of 5 stars5/5 (1)
- Basic Electric Circuits: Pergamon International Library of Science, Technology, Engineering and Social StudiesFrom EverandBasic Electric Circuits: Pergamon International Library of Science, Technology, Engineering and Social StudiesRating: 3 out of 5 stars3/5 (1)
- Physical Electronics Slides of Chapter 3Document31 pagesPhysical Electronics Slides of Chapter 3anesseNo ratings yet
- ECE101 Modules 1& 2 Semiconductor Theory DiodeDocument47 pagesECE101 Modules 1& 2 Semiconductor Theory DiodeChariza MaicoNo ratings yet
- UES012 - Electrical PropertiesDocument17 pagesUES012 - Electrical PropertiesKunwar Achint SinghNo ratings yet
- Physics Question BankDocument8 pagesPhysics Question Bankkrishnaharee014No ratings yet
- Chapter 27-Current and ResistanceDocument21 pagesChapter 27-Current and ResistanceGled HysiNo ratings yet
- The Elusive Memristor: Properties of Basic Electrical CircuitsDocument24 pagesThe Elusive Memristor: Properties of Basic Electrical CircuitsKapil BhardwajNo ratings yet
- Electron TheoryDocument13 pagesElectron TheoryAilene Tsui Alferez PaciaNo ratings yet
- Electronics-Telecommunication Paper 1 ObjectiveDocument43 pagesElectronics-Telecommunication Paper 1 ObjectiveMathews PaulNo ratings yet
- Electronic Devices and CircuitsDocument377 pagesElectronic Devices and CircuitsJermaine Strachan50% (2)
- Bonding Forces in SolidsDocument81 pagesBonding Forces in SolidsPratheeksha GowdaNo ratings yet
- A Seminar ReportDocument30 pagesA Seminar ReportSanthanu Surendran100% (1)
- Scanning Tunnelling MicroscopeDocument37 pagesScanning Tunnelling MicroscopeMerve Ayvaz KöroğluNo ratings yet
- Witricity Seminar ReportDocument8 pagesWitricity Seminar ReportMohammed MusifNo ratings yet
- Project Searchable PDFDocument17 pagesProject Searchable PDFPratyushNo ratings yet
- Nano 2001 966384Document6 pagesNano 2001 966384GoxseNo ratings yet
- Model Paper-3: Section - BDocument3 pagesModel Paper-3: Section - BAnil Mudhiraj ChennuboinaNo ratings yet
- Inter 2nd Year PhysicsDocument14 pagesInter 2nd Year PhysicsRsp Srinivas80% (10)
- EDC Notes PDFDocument377 pagesEDC Notes PDFscribdcurrenttextNo ratings yet
- Nanoassignment V2Document6 pagesNanoassignment V2Shadman SaquibNo ratings yet
- Single Electron TransistorDocument11 pagesSingle Electron TransistorHarsha VardhanNo ratings yet
- Dr. Nasim Zafar: COMSATS Institute of Information Technology Virtual Campus IslamabadDocument43 pagesDr. Nasim Zafar: COMSATS Institute of Information Technology Virtual Campus Islamabadrizwanspirit11No ratings yet
- Department of Automobile Engineering IV Semester: Ec6464 Electronics and MicroprocessorsDocument77 pagesDepartment of Automobile Engineering IV Semester: Ec6464 Electronics and MicroprocessorsDinesh KannaNo ratings yet
- Modern Physics - Chapter 25Document83 pagesModern Physics - Chapter 25Hamza PagaNo ratings yet
- EDC Notes PDFDocument377 pagesEDC Notes PDFramyadspNo ratings yet
- FormulaDocument7 pagesFormulahelenarajNo ratings yet
- Factors Affecting Internal Resistance emDocument14 pagesFactors Affecting Internal Resistance emAman DixitNo ratings yet
- Physics Theory-FinalDocument26 pagesPhysics Theory-Finaladibsadman10No ratings yet
- 6 Chap 8 Magnetic Forces Class P2Document68 pages6 Chap 8 Magnetic Forces Class P2sulaymansyed11No ratings yet
- PH8253 Physics For Electronics EngineeringDocument89 pagesPH8253 Physics For Electronics EngineeringSindia FeliciaNo ratings yet
- Physics 12thDocument15 pagesPhysics 12thprashanthm1398No ratings yet
- EC6464 Electro Micro Proc Notes (Typed)Document77 pagesEC6464 Electro Micro Proc Notes (Typed)DolianNo ratings yet
- Class 12 Physics Current Electricity QBDocument99 pagesClass 12 Physics Current Electricity QBRakesh AgarwalNo ratings yet
- ၂၀၁၄ တကၠသိုလ္ဝင္စာေမးပြဲ မေကြး ႐ူပေဗဒေမးခြန္းDocument4 pages၂၀၁၄ တကၠသိုလ္ဝင္စာေမးပြဲ မေကြး ႐ူပေဗဒေမးခြန္းKyi Htin PawNo ratings yet
- Ec 6403 - Electromagnetic FieldsDocument24 pagesEc 6403 - Electromagnetic FieldsMs.V.Sangeetha Poorani Assistant ProfessorNo ratings yet
- Physics Investigatory 2 PDF FreeDocument24 pagesPhysics Investigatory 2 PDF Freethevloger007No ratings yet
- Transistors: The Commonwealth and International Library: Selected Readings in PhysicsFrom EverandTransistors: The Commonwealth and International Library: Selected Readings in PhysicsNo ratings yet
- Tugas 3 Pengukuran ListrikDocument6 pagesTugas 3 Pengukuran ListrikPutraNo ratings yet
- Preboard Physics 2023-24Document5 pagesPreboard Physics 2023-24rishitasarkar875No ratings yet
- Second Semester Physics - 2 Two Marks With Answers Regulation 2013Document9 pagesSecond Semester Physics - 2 Two Marks With Answers Regulation 2013PRIYA RAJINo ratings yet
- BEF22903 Chapter 2Document35 pagesBEF22903 Chapter 2rajsathia99No ratings yet
- Submodule5 Sampling Designs Ver3 29nov2018Document26 pagesSubmodule5 Sampling Designs Ver3 29nov2018Patricia FloresNo ratings yet
- 071 - Data Sheet UpsDocument15 pages071 - Data Sheet UpsbilalNo ratings yet
- Literature Review On Stress Among DoctorsDocument5 pagesLiterature Review On Stress Among Doctorsea8142xb100% (1)
- Amplivox CA850 Series 3 Operating Manual Issue 11Document26 pagesAmplivox CA850 Series 3 Operating Manual Issue 11PraistonNo ratings yet
- MTK 1043 Smaw 1Document22 pagesMTK 1043 Smaw 1Mohd Dinie HafiqNo ratings yet
- Plant QRQC FormDocument1 pagePlant QRQC FormJordi Palomar100% (5)
- 5988 6917enDocument7 pages5988 6917enИван КумбровNo ratings yet
- Hager EG100 Timer User ManualDocument2 pagesHager EG100 Timer User Manualmcprinter100% (1)
- MSDS Antox 71e1Document15 pagesMSDS Antox 71e1Kumar RamanNo ratings yet
- Japan 2024 ItineraryDocument3 pagesJapan 2024 Itineraryleaann.tawayNo ratings yet
- National Transmission Corp. v. de Jesus PDFDocument4 pagesNational Transmission Corp. v. de Jesus PDFJerald Oliver Macabaya0% (1)
- 1001bit Pro Installation Guide PDFDocument7 pages1001bit Pro Installation Guide PDFGen PtNo ratings yet
- Bail PDFDocument2 pagesBail PDFSahidul IslamNo ratings yet
- United States v. Travis Robinson, 4th Cir. (2012)Document4 pagesUnited States v. Travis Robinson, 4th Cir. (2012)Scribd Government DocsNo ratings yet
- Bluedio H+ User Manual 2014-12-21 19-49Document4 pagesBluedio H+ User Manual 2014-12-21 19-49pat535550% (8)
- Preguntas Norma API 675Document3 pagesPreguntas Norma API 675Diego Rodriguez0% (1)
- An Evaluation On The Cleanliness HabitsDocument31 pagesAn Evaluation On The Cleanliness HabitsWilan PrincipeNo ratings yet
- Effect of Heat and Air On A Moving Film of Asphalt (Rolling Thin-Film Oven Test)Document6 pagesEffect of Heat and Air On A Moving Film of Asphalt (Rolling Thin-Film Oven Test)intanmizwarNo ratings yet
- Deltares License Management - Installation ManualDocument45 pagesDeltares License Management - Installation ManualAnne PutriNo ratings yet
- LOreal 2015 Annual Report PDFDocument60 pagesLOreal 2015 Annual Report PDFStefania ChristiNo ratings yet
- Hpc1: Kitchen Essentials and Basic Food Preparation: Talisay City CollegeDocument10 pagesHpc1: Kitchen Essentials and Basic Food Preparation: Talisay City CollegeDennice April AligangaNo ratings yet
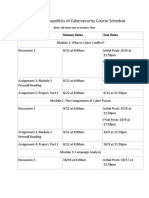
- PUBP 8823 - Geopolitics of Cybersecurity Course ScheduleDocument2 pagesPUBP 8823 - Geopolitics of Cybersecurity Course SchedulebillybobNo ratings yet
- 0.4mm, 0.5mm, 1mm Pitch, 1.2mm Above The Board, Flexible Printed Circuit & Flexible Flat Cable ZIF ConnectorsDocument16 pages0.4mm, 0.5mm, 1mm Pitch, 1.2mm Above The Board, Flexible Printed Circuit & Flexible Flat Cable ZIF ConnectorsAbdul HameedNo ratings yet
- BRIDGE-TO-INDIA Anti Dumping DutyDocument7 pagesBRIDGE-TO-INDIA Anti Dumping DutyAbhinav GuptaNo ratings yet
- Multimedia Design Project ReportDocument6 pagesMultimedia Design Project Reportapi-608836622No ratings yet
- B2B Market SegmentationDocument14 pagesB2B Market SegmentationHossam HashieshNo ratings yet
- The Executive Coaching HandbookDocument85 pagesThe Executive Coaching Handbookmarnit100% (4)
- Studi Lajut Dalam MakalahDocument7 pagesStudi Lajut Dalam Makalahb49usprasetyoNo ratings yet
- 24.air Interface ChannelsDocument2 pages24.air Interface Channelsdeepak19m100% (1)