Experiments in Chemical Engineering Binary Distillation

Experiment 1
BINARY DISTILLATION

INTRODUCTION
Distillation is one of the most important but also the most energy intensive separation
process that chemical engineers should be concerned about. Thus, a good understanding of the
theories and application of this unit operation is essential in order to minimize energy
consumption. There are many types of distillation operations, depending on the process
followed, the type of equipment and the number of volatile components present in the solution
to be purified. In this laboratory exercise the one using the concept of a binary equilibrium
relationship by operating a simple batch distillation set-up is investigated. The binary system
applied is ethanol-water where students will investigate the validity of the Rayleigh’s equation.

OBJECTIVES
The experiment is composed of two parts with the following objectives:
1. To investigate the applicability of the Rayleigh’s Equation to describe differential
distillation.
2. To determine the temperature and concentration profile in a differential distillation
process.

Unit Operations Laboratory Page 1

Experiments in Chemical Engineering Binary Distillation

THEORY
Distillation is a unit operation commonly used for purifying liquids and separating a
liquid mixture of miscible and volatile substances into individual components or, in some cases,
into groups of components. A liquid can be classified as volatile when it is readily vaporized at a
relatively low temperature. The boiling of the more volatile components of the mixture drives
the distillation process. When the vapor is cooled, the more volatile material condenses in a
greater proportion than the less volatile material.

The components are separated based on their physical properties, specifically, relative
volatilities. Relative volatility, a tool used to express the magnitude of the equilibrium
distribution, is defined as

(𝑦𝐴 ⁄𝑥𝐴 )
𝛼=
(𝑦𝐵 ⁄𝑥𝐵 )

where 𝛼 = Relative volatility

𝑦 = Vapor composition
𝑥 = Liquid composition
𝐴 = More volatile component
𝐵 = Less volatile component

There are two types of distillation classified according to its mode of operation. These
are continuous and the batch distillation. In a batch system, the column can handle different
mixtures by simply changing its operating conditions. The main disadvantage to using this kind
of system, however, is that the longer the components are exposed to high temperature, the
better the chances that the components are broken down via thermal degradation. Along with
this, the energy requirements are usually higher for a batch system. Conversely, continuous
distillation, as the name implies, feed is continuously supplied and separated into two or more
products over some period. On the other hand, batch distillation involves the processing of a
batch of feed at a given time and split into products by selectively removing the more volatile
fractions over time.

A. Differential Distillation

When a binary solution of volatile liquids is subjected to batch differential distillation,

the concentration of the solution in the distillery still decreases in the more volatile component
as the boiling point of the solution increases. The resulting vapor is allowed to condense
through a condenser and collected together as the distillate product.

Unit Operations Laboratory Page 2

Experiments in Chemical Engineering Binary Distillation

The problem in this case is to relate the initial amount of feed together with its concentration
and the amount of over-all distillate collected and its concentration.

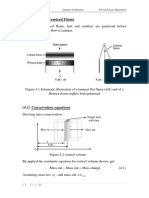
At any given time, the concentrations may be related by material balance. Referring to
Figure 1, if W is the amount in the still at any time of concentration x, a more volatile
component balance yields

X
𝑤𝑥 − (𝑤 − 𝑑𝑊)(𝑥 − 𝑑𝑥) = 𝑦𝑑𝑊
𝑤𝑥 − 𝑤𝑥 + 𝑥𝑑𝑊 + 𝑊𝑑𝑥 − 𝑑𝑊𝑑𝑥 = 𝑦𝑑𝑊
𝑊𝑑𝑥 = (𝑦 − 𝑥)𝑑𝑊
y
𝑑𝑊 𝑑𝑥
= dW
𝑊 𝑦−𝑥

x W-dW

Figure 1: Distillation System

Integrating, considering the initial feed as F and concentration xF,

𝑊 𝑥𝑤
𝑑𝑊 𝑑𝑥
∫ =∫
𝐹 𝑊 𝑥𝐹 𝑦 − 𝑥

𝑥𝐹
𝐹 𝑑𝑥
𝑙𝑛 = ∫
𝑊 𝑦−𝑥
𝑥𝑤

This equation is referred to as Rayleigh’s Equation. The instantaneous liquid

composition, x, and the corresponding vapor composition, y are assumed to be in equilibrium
with one another. Vapor Liquid Equilibria (VLE) data may be determined from Vapor-Pressure-
Temperature, Boiling Point Composition diagram or equilibrium data, or x-y diagram for the
binary system.

Unit Operations Laboratory Page 3

Experiments in Chemical Engineering Binary Distillation

The Rayleigh Equation may be simplified to various forms such as:

1. If Henry’s law applies, y = mx where m = H/P. The integrated equation yields

𝐹 1 𝑥𝐹
𝑙𝑛 = 𝑙𝑛
𝑊 𝑚 𝑥𝑊
this equation, however, is applicable only for dilute solutions, where the partial pressure of the
vapor is a linear function of composition.

2. If the relative volatility, 𝛼AB may be assumed practically constant then,

𝛼𝐴𝐵
𝑦=
(𝛼𝐴𝐵 − 1)𝑥 + 1
substituting this in the previous equation and integrating gives
𝐹 1 𝑥𝐹 1 − 𝑥𝑤
𝑙𝑛 = [𝑙𝑛 +̅̅̅̅̅̅
𝛼𝐴𝐵 𝑙𝑛 ]
𝑊 𝛼 ̅̅̅̅̅
𝐴𝐵 − 1 𝑥𝑤 1 − 𝑥𝐹
or in terms of individual components,
𝐴1 𝐵1
𝑙𝑛 = ̅̅̅̅̅
𝛼𝐴𝐵 𝑙𝑛
𝐴2 𝐵2
Subscript 1 refers to the initial amounts and subscript 2 refers to the final amounts
found in the solution. The amount of distillate may be determined by material balance together
with its composition.
If the above assumptions could not be applied, the best way to evaluate the integral of
Equation 2 is by graphical or numerical methods. The graphical method is shown in Figure 2.
1
Graphically, plot 𝑦−𝑥 versus x at different stages of the experiment to relate the amount
distilled at any time with composition and temperature by getting the area under the curve and
comparing this area and composition with the experimental data obtained. The validity of the
simplified equation may also be compare with the experimental data.

𝐹
𝐴𝑟𝑒𝑎 = 𝑙𝑛 𝑊
1
𝑦−𝑥

𝑥𝑤 𝑥 𝑥𝐹

Figure 2: Graphical Method

Unit Operations Laboratory Page 4

Experiments in Chemical Engineering Binary Distillation

EQUIPMENT
A. Actual Equipment

Control System

Packed Column

Boiler Still

Figure 3: Laboratory Distillation Column

B. Equipment Design

The equipment contains a 4-inch bubble cap batch distillation column which may be
operated under total or partial reflux conditions. Also used in this experiment is a
distillation column packed with glass beads for total reflux operations. As for the
determination of the refractive index, a refractometer was used.

Unit Operations Laboratory Page 5

Experiments in Chemical Engineering Binary Distillation

PROCEDURE
A. Preparation of a Calibration Curve

1. Prepare a 0, 10, 20, 30, 40, 50, 60, 70, 80, 90 (% v/v) ethanol solution.

2. Use the refractometer to determine the refractive indices of the different

solutions.

3. Plot the refractive index versus ethanol concentration.

B. Batch or Differential Distillation Experiment

1. Setup the batch distillation apparatus.

2. Make 10% ethanol (25 mL pure ethanol and 225 mL water).

3. Heat the setup until the first drop of condensate is collected. Record the initial
temperature reading and start the time.

4. For every 10 mL of condensate collected, record the corresponding time and

temperature.

5. Using a refractometer, determine the refractive index of the samples collected.

6. Repeat steps 4 and 5 until you have at least six runs or until 60 to 70% of the
solution is distilled.

Unit Operations Laboratory Page 6

Experiments in Chemical Engineering Binary Distillation

Binary Distillation

DATA SHEET
A. Calibration Data

Concentration of Concentration of
C2H5OH-H2O Refractive Index C2H5OH-H2O Refractive Index
(% v/v) (% v/v)
0 1.3325 60 1.3595
10 1.336 70 1.361
20 1.315 80 1.361
30 1.354 90 1.360
40 1.3555 99 1.3595
50 1.360

B. Batch Distillation

Condensate Bottom Sample Middle Sample

Volume Time
(mL) Temperature Refractive Temperature Refractive Temperature Refractive (min’sec’’)
(°C) Index (°C) Index (°C) Index
1st drop 45 0 45 0 45 0 -----
10 88 1.361 75 1.34 65 1.3615 1’08’’
20 88 1.3615 78 1.339 75 1.361 2’18’’
30 89 1.36155 83 1.3385 79 1.3605 3’30’’
40 90.5 1.362 85 1.338 83 1.36 4’49’’
50 92 1.3605 87 1.336 87 1.3585 6’14’’
60 94 1.36 89 1.3355 89 1.358 7’49’’
70 95 1.3585 91 1.334 92 1.355 9’37’’
80 96 1.354 93 1.3333 94.5 1.35 11’39’’
90 98 1.348 94 1.3333 96.5 1.345 13’58’’
100 98 1.339 95 1.3326 98 1.3385 16’24’’

Unit Operations Laboratory Page 7

Experiments in Chemical Engineering Binary Distillation

GUIDE QUESTIONS
1. Plot the calibration curve as refractive index versus ethanol concentration.
2. Derive a correlation equation for refractive index as a function of concentration.
Comment on the usefulness of this correlation. What is the range of concentration that
generates the smallest and largest deviation?
3. Plot the F/W and the experimental ratio F/W versus the concentration of the residue.
Describe the results. Is there good agreement between the experimental results with
those obtained by Rayleigh’s equation?
4. Compare the experimental amount of total collected with the theoretical results using
the graphical method of solution and using the average relative volatility during the
entire differential distillation process. Tabulate and indicate the percent deviation.

ANALYSES AND CALCULATIONS

Unit Operations Laboratory Page 8

Experiments in Chemical Engineering Binary Distillation

APPENDIX

Unit Operations Laboratory Page 9