Definition 1.

A function f : D ⊆ R2 → R means a rule that assigns to each

(x, y) ∈ D a unique real number z := f(x, y)1. We call D the domain of f. 2

In the definition of function we have that its domain, D, is specified. But often
times, no mention of the domain of f is given. It’s customary in these cases to
take the domain of f to be the so called natural domain. The natural domain of
f : D ⊆ R2 → R is the largest subset of R2 such that f can be defined.
p
Example 1. What’s the natural domain of f(x, y) = 1 − x2 − y2 ?

Solution. We know 1 − x2 − y2 > 0 because of the square root. In other words,

1 > x2 + y2 . So the natural domain of f is

D = {(x, y) ∈ R2 : x2 + y2 6 1} ⊆ R2 .

Visually, D represents the interior and boundary of the circle of radius 1 centered
at the origin.

Problem 1. Can you find a function f : D ⊆ R2 → R such that the half annulus
D = {(x, y) ∈ R2 : 1 < x2 + y2 6 2, x > 0} is the natural domain?

It’s helpful and natural to visualize functions of several variables. So, we intro-
duce a straightforward definition of the graph of f.

Definition 2. The graph of f : D ⊂ R2 → R means the set of all points (x, y, z) ∈

R3 such that (x, y) ∈ D and z = f(x, y).

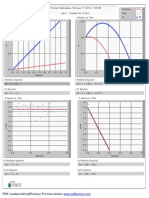
Example 2. Below is the graph of f : D ⊂ R2 → R where D is the set of (x, y)

satisfying −1 6 x, y 6 1 and f(x, y) = x2 + y2 .
-1.0
-0.5
0.0
0.5
1.0
2.0

1.5

1.0

0.5

0.0
1.0
0.5
0.0
-0.5
-1.0

1In layman’s terms, the notation f : D ⊆ R2 → R just means f is a function with two inputs

coming from D and one output

2This definition easily extends to many variables, e.g., f : D ⊂ R3 → R means a rule assigning

to each (x, y, z) ∈ R3 a unique w := f(x, y, z)

1
2

In order to facilitate the visualization process, we introduce the concept of a

level curve.

Definition 3. The level curve at k of a function f : D ⊆ R2 → R is the set of all

points (x, y) ∈ R2 satisfying f(x, y) = k.

Geometrically speaking, the level curves are the cross sections of the graph of f
with planes parallel to the x, y-plane, namely, the planes z = k.

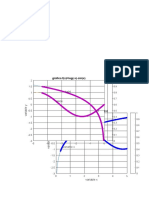
Example 3. Graph the level curves at k = 0, 1, 2 for f(x, y) = xy on the same

coordinate axis.

Solution. For k = 0, the level curve at k is the set of all (x, y) satisfying xy = 0.
In this case, it must be that either x = 0 or y = 0. So the level curve at k = 0 of f
consists of the x and y axes.
For k = 1, we get xy = 1, i.e., y = 1/x. And for k = 2, we get y = 2/x. The
level curves (and graph of f with planes z = 0 and z = 2) are pictured below.

-3 -2 -1 1 2 3

-2

-4

√ p
Problem 2. What’s the level curve at k = 1/ 2 of f(x, y) = cos( x2 + y2 )?

(Challenge) Problem 3. Let f : R → R and let g : R2 → R be defined by

p
g(x, y) = f( x2 + y2 ). How is the graph of g related to the graph of f?