Professional Documents
Culture Documents
Simulation of Potassium Nitrate Sugar Ro PDF
Simulation of Potassium Nitrate Sugar Ro PDF
Uploaded by
Furkan ÖztürkOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Simulation of Potassium Nitrate Sugar Ro PDF
Simulation of Potassium Nitrate Sugar Ro PDF
Uploaded by
Furkan ÖztürkCopyright:
Available Formats
SIMULATION OF
POTASSIUM NITRATE – SUGAR
ROCKET MOTORS
Antoon (Tony) VYVERMAN6
Introduction
At the end of seventies the state of KNO3-sucrose research by BVRO (Belgian
Association For Rocket Research) was described in the Youth & Space book “The
Potassiumnitrate-sugar propellant”1. At the beginning of the nineties this led first at
NERO (essentially by John Koster) and later at VRO (under the impulse of Jan
Volckaert) to the development of new motors based on potassium nitrate (KNO3). In the
mean time a large number of tests have been realized (more than 60) and KNO3 based
motors were used for flight
purposes. The most spectacular
one for VRO being the Golden
Sky, measuring 2.5 m long with
a diameter of 0.16 m and a total
weight of 30 kg. The rocket
reached 2.4 km and the whole
flight was filmed from inside of
the rocket.
The large number of data
generated by all these tests give
us the possibility to review the
functioning of these motors. This
would not be necessary if these
motors would behave as
expected. In many cases the
measured thrust and pressure
diagrams do deviate strongly
from expectations. It is worth
trying to understand the
phenomena which occur in these
motors.
In the first place we want to draw
the attention to the following
differences between the 3 motor
types:
1. BVRO: although tests with sorbitol and mannitol were preformed back in the
seventies, mostly KNO3-sucrose (60/40) was used. Two different approaches were
followed :
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com 1
(a) The liquefied propellant was centrifuged in the coated motor. To assure a
throughly connection between the coating and the propellant grain, a
mixture of sucrose and salt, and in some cases only sucrose was used for the
coating. Also the coating was centrifuged. In this way grains with a central
cylindrical hole were realized.
(b) The liquefied propellant was pored in the coated motor provided with a
cylindrical or cruciform central mandrel, which was withdrawn after full
solidification.
Apart from the first few tests all propellant blocks were case bond.
2. John Koster used exclusively KNO3-sorbitol in a ratio of 60/40, pored directly
into the non-coated rocket motor provided with a cylindrical mandrel. Afterwards a layer
of epoxy covered the nozzle end surface of the grain. So also the NERO motors were of
the case bond type but without coating near the wall site.
thrust (N) curves NX- VOX
4500
4000 NX-21
3500
NX-
NX-22 12
3000 NX-
13
2500 NX-
NX-18 14
2000 NX-
NX-19 16
NX-
1500
18
NX-16 NX-
1000 NX-12
NX-13
500
0
0 0,5 1 1,5 2 2,5 3 3,5
THRUST CURVES ST 21- 40
ST-36
ST-38
1200
ST-21
1000
800
ST-31 ST-29
600 ST-25 ST-23 ST-32
ST-27 ST-34
400
ST-40
200
0
0 1 2 3 4
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com 2
3. Jan Volckaert from VRO uses a mixture of KNO3-sucrose-sorbitol in the ratio of
67.5/17.5/15, and makes use of several modules, some made of an aluminum tube, coated
with silicon on the inside. The grains have a cylindrical perforation. Up to 3 modules are
used in a Bates configuration.
A Bates motor is expected to deliver an almost flat curve. A typical Bates curve is NX-
13. From a grain that only burns from the inside to the outside (NERO) one can expect a
continuous increase of the thrust, like ST-32. From the different thrust diagrams it is
however clear that this is not always the case. At first sight there seems to be no logic
behind it. The ratio of the initial burning area to the throat area is not always the
determining factor in performance prediction!
The computer program
To be able to verify what is actually happening, a computer simulation program was set
up. This program allows the following simulations:
- the use of several modules, with two possibilities: a) no burning of the top and
bottom sites , b) burning at all none coated sites (Bates),
- cylindrical or crucifix shaped voids
- creation of cracks, partially or totally, at any time during burning (in the program
these cracks go all the way through the grain)
- erosion
- ignition delay
- initial ignition
With erosion we mean the situation where the regression of the burning surface is faster
than normal due to the high velocity flow of the reaction products over the burning
surface. In our program we have used the following factor to the burning rate:
(1+ erosion coefficient x gas speed)
For the calculation of the burning rate (without erosion) use is made of the so-called St.
Roberts burning law.
r = b + kP n
In order not to complicate too much the simulations, “b” was always taken zero.The
consequence of erosion is that the regression of the burning surface will not be the same
at all locations in the grain. Some parts will burn away much faster than others, such that
the void will soon deviate from a cylindrical shape. To cope with this effect the
propellant length was divided into 50 segments of constant velocity.
The program also takes into account the changing situation of pressure and free volume.
What is not taken care of is the pressure drop over the grain from bulkhead to nozzle.
For the thermodynamic values of the reaction products (molecular weight, temperature,
ratio of the specific heat,…) the results from GUIPEP are used. The fact that accoding to
the GUIPEP calculations a large part of the reaction products probably consists of
condensable material (mainly K2C03) is taken into account.
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com 3
The results from the NERO motors
Let us first look at the results from the NERO motors. The next diagrams give the
measured and the simulated thrust calculated with the computer program. As one can see
that the results are quite reasonable, taking into account the fact that the parameters have
to be found through trial and error. Also the fact that the used burning rate law will not be
correct over the whole pressure range contributes to the deviation. Richard Nakka2 has
proven that the burning rate of KNO3-sorbitol mixtures (in any case for 65% KNO3-
sorbitol) is very irregular. Also the erosion formula may not be sufficiently accurate.
Finally, irregularities in the grain like differences in the density of the grains and air
bubbles, or differences in KNO3 concentrations may occur. Important is to show the
tendencies in the thrust curves.
In the different thrust curves the actual values of the rocket (density of the propellant,
length of the grain(s), inner and outer diameter of the grains,) are used and the best fitting
values for “k” and “ε” (for erosion) are searched. “n” was taken at 0.41, because this is
the exponent which was derived from the BVRO tests. Maybe n = 0.31 or 0.32 could
have been a better choice. This is also the exponent found by Nakka for 65% KNO3 and
35% sucrose.
Whenever felt necessary to explain the curves, cracks were introduced. As everything
was done with trial and error better parameters can certainly be found.
From the simulation one can see that ST 32 is quite normal. This is not the case for ST 21
where 3 cracks occurred after about 0.3 s, and ST 36 with even 6 cracks. One has to keep
under consideration that when cracks are simulated, they are situated at equidistances. In
reality it may well happen that one crack is situated closer to the other. Also cracks are
considered to happen all over the thickness of the grain, although this need not be the
case in reality.
Simulation ST32
700
measured thrust N
600 1
2 simulated thrust
500
400
300
2
200
1
100
0
0 0,5 1 1,5 2 2,5 3 3,5
Not all-19 measurements of John Koster’s motors have been analyzed. Such an analysis
is very time consuming and not always necessary for our conclusions.
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com 4
1400
Simulation ST-36
1200
1000
800
F in N
600
400
200
0
0 0,5 1 1,5 2 2,5
We come to the following results:
ST-21 ST-32 ST-36
k 0.0014 0.0016 0.00135
n 0.42 0.42 0.42
ε 0.005 0.004 0.006
The erosion is important and will, essentially at the start when the inside diameter is still
small, generate high burning rates. They can go up till about 2 times the normal value.
Gas speeds of more than 100 m/s are found in the initial phase of burning. This means
that when the burning rate at the front site is 10mm/s, the burning rate at the nozzle site
becomes 20 mm/s. As a consequence the cylindrical void soon turns into a conical shape
and the flames will reach the wall at the nozzle site much sooner than at the bulkhead
site. The thrust curve reaches a maximum much sooner than expected, but the total
duration will remain as long as in a normal case, since this is determined by the burning
rate of the grain close to the bulk head, which is not subjected by erosion.
The reason why the NERO motors give such a wide range of results has probably to do
with a too low ratio of the inner diameter to the outer diameter of the grain. Indeed in
case bond propellants large tensile strengths can occur at the inside of the grain. This
phenomena is essentially determined by the above mentioned ratio and the Poisson
number of the material. This is clearly demonstrated by the following figure with gives
the internal tress as a function of both parameters.3 The upper series of curves give the
tangent stress at the inner side of the cylindrical void. Each curve corresponds to a given
Poisson ratio (ratio between shrinkage and elongation). The horizontal axis gives the ratio
between inner and outer diameter. When the inner diameter is very small, the ratio
between inner stress and pressure approaches 1, meaning that the stress is almost equal to
the gas pressures. The smaller the Poisson number the larger the stress at any given ratio
of inner to outer grain diameter. To be save this ratio should lie between 0.4 for a Poisson
number of 0.45 and 0.8 for a Poisson number of 0.3. For KNO3 propellants the Poisson
number is not known. As a general rule the inner diameter should be about half the outer
diameter. In the NERO motors the ratio of the inner to the outer diameter is situated
between 3.4 and 3.7. This yields stresses between 0.2 an 0.6 times the gas pressure in the
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com 5
motor. Although the tensile strength measured by Nakka is about 7.6 N/mm² (for KN-
sorbitol 65/35 at a density of 1820 kg/m³), cracks can occur much sooner due to lack of
elasticity of the material. In the seventies the occurrence of cracks was already described
in KNO3-sucrose propellant grains as a possible explanation of the observed results with
these motors. That some grains, with a too low value of the ratio of inner to outer grain
diameter, sometimes escape from cracks, is probably due to the fact that, thanks to a low
ratio of inner grain surface to throat area, only low initial pressures are built up, which
keeps the internal stresses within save limits.
The bottom series of curves give for the same Poisson number the tangent stress at the
outer diameter (against the wall). Negative values mean compression of the grain.
Stress in cylindrical case-bond grains
1
0,8
negative: compression / postive
0,6
0,4
0,2
stress
0
-0,2 0 0,2 0,4 0,6 0,8 1
0.30
-0,4 0.35
0.40
-0,6
0.45
-0,8
-1
ratio of inner to outer diameter
The results from the VRO and KAPPA motors
The VOX-motors have a ratio of internal diameter to outside diameter of 0.47 to 0.54.
This means that they are situated in the relatively safe region where compression is more
likely than stress. The VOX motors use a conception, which is beneficial to avoid
important stress. Separate modules are used which allow counter pressure of the
combustion gases at their outer surface. As a consequence all sides of the grain are
subjected to the same pressure. As the envelope is weaker the grain is less subjected to
stress and becomes a freestanding grain. Hence a weak but good heat resistant coating is
to be preferred above a strong coating which does not allow compression.
We will discuss now 3 simulations each with a specific character. Because of its nearly
ideal behavior NX-13 is a good reference. The simulation of the NX-13 is almost perfect
with the following parameters:
- k = 0.0026 m/s
- n = 0.32 (this is arbitrary chosen)
- ε = 0.005 – 0.007
- ignition delay = 0.25 s (m=1)
- initial ignition = 40%
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com 6
The last 3 values need clarification. The tail off of the thrust curve determines to a
certain extend the erosion coefficient. When the burning surface reaches the wall at the
same moment everywhere, the tail-off is very short and is only determined by the gases
left over in the rocket motor at that moment. Erosion creates a conical shape of the
grain, such that some parts of the burning surface closer to the nozzle, reach the wall
sooner than other parts. The consequence is a longer tail off.
The curves of the NX and to an even stronger extend, the KAPPA2, cannot be
explained without the assumption that the full burning surface of the grain is not ignited
at ones and that an ignition delay occurs. In our simulation we start from the idea that
part of the grain already burns when the diaphragm burst. This we call here “initial
ignition”. Since the grain is divided into 50 equal parts, an initial ignition of 40%
means that only 40% of the surface is ignited at the start.
In the simulation program the delay caused by the incomplete ignition of the grain is
calculated as follows: when the number of the grain part (numbered 1 to 50), is larger
than the value derived from the following formula,
time m * ignition delay + initial ignition
there is no ignition of that part of the grain. Within a certain delay, all parts of the
propellant grain will ignite.
VOX 22 simulation
3500
3000
simulated thrust"
2500 measured thrust
2000
thrust N
1500
1000
500
0
0 0,5 1 1,5 2 2,5 3
The simulation of the NX-22 is given. The NX-22 was chosen because it is very
representative for the VOX motors. From the simulation one can see that in reality the
digressive part of the curve is situated at somewhat higher values. When the thrust gets
its downward knick (at about 1.3 s), the burning surface at the nozzle site of the grain
has reached the wall and the shape of the grain is more or less conical. Following results
have been obtained:
- k = 0.0028 m/s
- n = 0.32
- ε = 0.025
- ignition delay = 0.61 s (m=0.3)
- initial ignition = 16
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com 7
The NX-21 is largely different from the other curves. Only one reasonable explanation
could be found: the different propellant modules do not burn at the top and bottom
surfaces, but only at the inside. But does it make any sense to suppose that some parts of
the surface do not burn at all? In any motor it takes some time to get the total burning
surface ignited.
From the KAPPA motor it is known that ignition takes place at the bulkhead such that
flames can reach the whole surface (probably with the exception of the top and bottom
surfaces of the individual grains). In both the KAPPA and VOX motors it takes some
time ( 0.25 to 0.8 s) before normal thrust is reached. From tests with the VOX it is
known that a more powerful igniter indeed results in a faster initial thrust increase. So
the ignition systems plays a very important role. But between slow ignition and no
ignition at all there is much difference. Some parts of the surface seem to ignite later
than others. This is also the point of view of Hans Olaf Toft, from the Danish rocket
club DARK, who performed a simulation of the thrust of the KAPPA. In his approach
the thrust curve can be completely explained by this effect. According to this theory, the
grain module closest to the nozzle, ignites first, than the second, the third and finally
after about 0.8 s the module near the bulkhead is completely ignited. This could be a
possible explanation for the sometimes-stepwise shape of the digressive phase (the
phase we still have some problems with). One can image the thrust curve to be made up
from a number of thrust curves generated by the different modules, shifted in time
through ignition delay. However, if this where the only reason as Toft suggests, than the
top of the curve should be determined by the theoretical combustion time for the
propellant module closed to the nozzle. Indeed, it is this module that first reaches the
wall according to his theory. As from that moment the thrust decreases. From
simulations based on the measured burning rate for 65% KNO3-35% sorbitol, it is
however clear that the top of the curve is too much to the right as compared to the
measured thrust curve (in other words it takes too much time). Only if also erosion is
assumed, we come to acceptable results.
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com 8
The simulation of KAPPA gives the following results:
- k = 0.0032
- n = 0.31
- ε = 0.008
- ignition delay = 1.17 s (m=1)
- initial ignition = 30%
Kappa KSB-001 simulation
2000
1800
1600
1400
Kappa01 sim thrust N
1200
Kappa02 sim thrust N
1000
800
600
400
200
0
0 0,5 1 1,5 2 2,5 3
In the diagram the simulation is represented for the case when all surfaces burn
(KAPPA 02) as for the case where no burning occurs at the top and bottom surfaces of
the 4 propellant grains (KAPPA 01).
The “k” and “n”-values for the burning rate are close to the measurements of Nakka.
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com 9
How to explain that the 65% KNO3 - 35% Sorbitol propellant is so difficult to ignite and
that in the NX-21, during more than 2.5 s, the top and bottom surfaces of the grains are
not ignited? There is more and more evidence now that KNO3-sorbitol propellants are
much more difficult to ignite than KNO3-sucrose mixtures. So it is not completely
unexpected that when instead of sorbitol alone, also a mixture of sorbitol and sucrose is
used, as in the NX motors, ignition problems occur. Moreover, it is possible that at
ignition, thanks to the low viscosity of liquid sorbitol and its resistance to
decomposition, a thin film of sorbitol is created on the outside of the grain. This thin
film may isolate the propellant surface and protect the KNO3 grain. It is also possible
that this thin sorbitol layer is created during manufacturing. To prevent this problem the
burning surface should be made rough (which is always a good procedure). Another
possibility is that liquid K2CO3 or KOH, produced during the combustion, condenses on
the “cold” and isolated surface of the grain.
The next figure shows how the burning surface progresses in time. The x-ax is the
length of the total grain (50 units), the y-axis the radius in m. The largest value is the
wall.
3,00E-02
2,50E-02
2,00E-02
1,50E-02
1,00E-02
5,00E-03
Progression of the burning surface
0,00E+00 with time
0 10 20 30 40
Not only there are limits for the inner diameter of the grains for case-bonded grains, also
the erosion puts limits. This time however to the total length of the grain. With
increased length of the grain (at constant internal cross section) the speed of the gases
will increase and consequently also the erosion. As a consequence, part of the wall (or
coating) will be unprotected for the flames. When neglecting the effect of erosion
during motor design, the chamber pressure can become unexpectedly large and even
lead to explosion.
What happened to the BVRO NEBEL2 motors in the seventies?
In the seventies BVRO experimented with 60% KNO3-40% sucrose case bond
propellant grains. One type of propellant grain was provided with a crucifix shaped
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com 10
hole, the other type with a cylindrical hole of different diameters, mostly prepared by
the centrifugation of the liquid propellant. Although most of the time these motors
worked very well, both types led to explosions. Most explosions occurred with the
centrifuged propellants.
For the thrust curves of the NEBEL motors with crucifix hole we did not succeed in
finding out how these grains actually burn. Several hypotheses were proposed, all based
on the occurrence of cracks in the propellant, but none gave satisfaction. Cracks were
supposed because they explained very well what happened in the motors with a
cylindrical hole, and a crucifix shaped hole was expected to generate important stress.
That we could not find the solution was quite remarkable, and frustrating, because this
type of motors produced all the time more or less the same shape. So there was
undoubtedly always the same thing happening. No cracks was not imaginable because
in that case the thrust had to show an increasing thrust curve, at least of a long period.
At that time we were convinced that erosion could not be the cause.
Based on the developed computer model first NEBEL 3 with cylindrical perforation was
recalculated. The thrust curve could be very well simulated without cracks and with
following parameters:
- k = 0.0029
- n= 0.32
- ε = 0.003 – 0.005
The values for “n” and “k” were used on NEBEL 2 were a good match was found if
several cracks occurred. Finally it was applied to grains with crucifix holes. It was
shown that with increasing value of the erosion coefficient “ε”, curves of the type
NEBEL 8 (ε = 0.02), NEBEL 6 (ε = 0.04) and NEBEL 9 ( ε = 0.045) were generated.
Contrary to what was thought during such a long time, these motors behave “normal”,
that is without cracks.
The reason for the very strong erosion may be found in the high ratio of total burning
surface to the cross section area of the void (65 to 70). After about 0.3 to 0.5 seconds
the burning surface reaches the wall at the nozzle side. The burning rate during that
period ranges between 3 to 5 cm/s or 2 to 4 times faster than the burning rate without
erosion. As one can see the simulation of the NEBEL motors is of very good quality.
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com 11
Simulation NEBEL 6
4000
3500
simulation
3000
measured thrust
2500
2000
1500
k=0.00275 m /s
1000 n=0.32
e=0.04
500 initial iginition=30%
ignitiondelay=0.25s
0
0 0,2 0,4 0,6 0,8 1 1,2 1,4
This however does not solve the problem of the explosions. In 1978 out of a series of 4
NEBEL motors, 3 exploded one after the other. From these NEBEL motors one was
provided with a crucifix shaped hole (NEBEL 10 a rocket intended to flight, but
exploded during the first moments of lift-off), and 3 (NEBEL 11, 12 and 13) provided
with a cylindrical hole, manufactured through centrifugation. In all exploded motors, the
propellant density was extremely low: 1.54 – 1.57. From centrifuged propellant grains
one can expect the density to decrease with decreasing radius because of lower
centrifugal forces. Whether KNO3, which is heavier than sucrose, migrates towards the
outer regions of the grain has never been measured. If this happens it would contribute
to even higher differences in density over the radius. Knowing that the burning rate
increases with decreasing density, and that strength decreases, may explain much. One
NEBEL explosion, NEBEL 7 (crucifix), has another reason. The motor worked
perfectly till about 0.75 s. The reason for explosion here lays probably in the used
coating. After 0.75 s a large part of the propellant is already consumed and the flames
have reached the coating over a certain distance. Since at that time we used sucrose as
coating material (because it would perfectly integrated with the propellant), it is highly
probable that this material, becoming quickly liquid, has been driven to the nozzle
where it blocked the throat. On the pressure and thrust diagram a sudden drop in thrust
goes together with a steep rise in pressure. This kind op problems can easily we solved
when using other liners.
Somme concluding remarks:
- characteristic velocity:
For the different propellant formulations used and discussed in this article we have the
following values of the characteristic velocity:
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com 12
Propellant composition Theoretical Measured characteristic
characteristic velocity velocity
m/s m/s
65 % KNO3-35% sucrose 1003.5 -
60% KNO3-40% sucrose 9914 979
65% KNO3-35% sorbitol 938 8805
60% KNO3- 40% sorbitol - 797
The characteristic velocity is a value which only depends upon the propellant and its
chemical reaction efficiency, and not on the conversion in the nozzle.
The use of sorbitol:
The use of sorbitol as fuel, alone or in combination with sucrose has positive and
negative effects.
Negative:
- Decrease in specific impulse.
- increased ignition problems
- lower density: sorbitol: 1.489 , sucrose: 1.58
- if only sorbitol is used (at least for 65/35), the burning rate- pressure relation is not a
smooth curve, instead it shows plateau’s and dips.
Positive:
- decrease in melting temperature. Sorbitol melts at 110°C while sucrose melts at
185°C.
- On the other hand the use of sucrose makes the propellant very hygroscopic and
makes storing over large periods difficult.
- Densities are closer to the theoretical values (see also table)
The increase of KNO3 content also increases the content of condensable material
(K2CO3 and KOH). The usage of nozzles with very small divergent angle (7 – 8°) may
increase the specific impulse, although no tests have been reported so far.
The density of the propellant:
It is interesting to have a look at the values for the density:
Composition Theoretical Measured Difference % source
67.5 KNO3 – 17,5 sucrose – 15 % sorbitol 1.88 1.72 8.5% VRO -VOX
65 KNO3- 35 % sorbitol 1.84 1.82 1.1% NAKKA
65 KNO3 – 35 % sucrose 1.89 1.80 4.8% NAKKA
60 KNO3-40% sorbitol 1.81 1.72 5% NERO
60% KNO3-40% sucrose 1.86 1.66 10.7% BVRO ‘70-’80)
It is clear that in all cases Nakka comes to the highest densities, essentially for 65%
KNO3-35% sorbitol, he gets extremely good figures. Higher density gives better
mechanical strength. It probably also influences the burning rate: it can be expected that
lower density propellants burn faster than high density ones. The figures also show
clearly that in the seventies the BVRO had poor control over the density (in some
motors we only got 1.54 or 17% deviation from the theoretical value), which is probably
the reason for some malfunctions.
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com 13
The burning rate of the different propellant compositions:
The simulations allow us to compare the burning rate (without erosion) of the different
propellant compositions. What we find is in good agreement with what can be expected
in general:
- higher KNO3 content (until a maximum value) will increase the burning rate.
- higher sorbitol content decreases the burning rate.
The propellant composition 65% KNO3-35% sucrose (as measured by R.Nakka) gives
the highest burning rate. 60% KNO3 – 40% sorbitol gives the lowest rate. The other
compositions are situated in between both rates. 67.5 KNO3- 17.5 sucrose-15% sorbitol
(simulation) is situated in between 65% KNO3- 35 % sucrose and 65% KNO3-35%
sorbitol. Hence, the amount of sorbitol (15%) decreases the burning rate more than the
increase (2,5%) in KNO3. The situation of the burning rates is a good indication of the
reliability of the simulation method used. At the same pressure, the highest burning rate
is about 2 times larger than the slowest! The specific impulse of 65% KNO3-
35%surcrose and density are also higher.
Propellant k in m/s n
composition (pressure in
bar)
65 KNO3 – 35 % sucrose 0.00395 0.319
65 KNO3- 35 % sorbitol 0.0032 0.31
60% KNO3-40% sucrose 0.0029 0.32
67.5 KNO3 – 17,5 sucrose – 15 % 0.0027 0.32
sorbitol
60 KNO3-40% sorbitol 0.0014 0.41
KNO3-sugar propellants
burning rate from thrust curve
18 simulation
4
16
14
5
2
12
3
burning rate mm/s
10
1
8
KNO3-sorbitol 60/40
4
KNO3-sucrose 60/40
KNO3-sucrose-sorbitol 67.5-17.5-15
2 KNO3-sucrose 65-35
KNO3-sorbitol 65-35
0
0 20 40 60 80 100
pressure bar
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com 14
It should be emphasized that the burning rate trajectories are only global. It should be
remembered that we started from the St.Roberts equation for the whole trajectory. As
has been demonstrated by Nakka, some propellants not always obey this law.
1
. “The Potassiumnitrate-sugar propellant” Tony Vyverman, Youth & Space 1978 (available at www.VRO.be or
Chris.Steyaert@vvs.be ). This book contains details about the NEBEL motors and many other experiments with
this propellant.
2
www.nakka-rocketry.net. This excellent website contains a wealth of information about potassium nitrate
sugar propellants
3
“Fabricage en mechanische eigenschappen van een vast brandstofblok” Chris Steyaert – BVRO Bulletin 1978
4
In the “The Potassiumnitrate-sugar propellant” book a thermodynamic calculation of the propellant was made.
It was assumed at that time that K2CO3 is decomposed at the conditions in the rocket motor and hence not
produced during combustion, in contradiction with the GUIPEP calculations. This assumption was taken
because of the large gap between the theoretical calculations with formation of K 2CO3 (like GUIPEP does) and
the measured results and because of the similarity of K2CO3 to CaCO3, with almost the same melting point,
which decomposes completely. The value of 994 m/s for the characteristic velocity of 60%KNO 3-40%sucrose
was obtained under this assumption. For 65%KNO 3-35%sucrose, GUIPEP predicts a specific impulse of 166 s
while the measured specific impulse is about 130 s. The values for the other compositions were calculated with
GUIPEP.
5
This value was calculated by the author based on the pressure curve from the KAPPA002 test.
6
email address: ascent.bvba@pandora.be
PDF created with FinePrint pdfFactory trial version http://www.fineprint.com 15
You might also like
- Rocket and Space Propulsion - Unit 1Document20 pagesRocket and Space Propulsion - Unit 1Lokanand DharmentharNo ratings yet
- FRR FinalDocument80 pagesFRR Finaldth1933No ratings yet
- Minotaur PDFDocument69 pagesMinotaur PDFbospankerNo ratings yet
- Solid RocketDocument18 pagesSolid RocketVincent S Ryan100% (7)
- Rocket Altitude Prediction ChartsDocument45 pagesRocket Altitude Prediction ChartsAviation/Space History Library100% (1)
- Analysis of Racecar ChassisDocument39 pagesAnalysis of Racecar ChassisMichelle Morrison100% (6)
- The Universal Bible: The Universal Truth of The BibleDocument125 pagesThe Universal Bible: The Universal Truth of The Bibledao einsnewt100% (4)
- Flyduino KISS Flight Controller V2 Manual: Image: Upper / Top SideDocument19 pagesFlyduino KISS Flight Controller V2 Manual: Image: Upper / Top SideBruno MarcheseNo ratings yet
- Low-Reynolds-Number Airfoil DesignDocument9 pagesLow-Reynolds-Number Airfoil Designamir_karimiNo ratings yet
- SugarPro ProposalDocument37 pagesSugarPro ProposalJose Miguel Berrios100% (1)
- Rocket 1Document132 pagesRocket 1Vincent S Ryan100% (3)
- Rocket Motor Construction TutorialDocument19 pagesRocket Motor Construction TutorialAzher Uddin100% (1)
- Solid Rocket MotorDocument15 pagesSolid Rocket MotorVsm Krishna Sai EturiNo ratings yet
- Block FoundationDocument18 pagesBlock Foundationvenkatesh1970150% (2)
- Build A Rocket AltimeterDocument9 pagesBuild A Rocket AltimeterMisesWasRight100% (1)
- Design Optimization of Solid Rocket Motor GrainsDocument184 pagesDesign Optimization of Solid Rocket Motor GrainsJamal Alshawesh100% (1)
- Solid Rocket MotorDocument26 pagesSolid Rocket Motoranon_149673746No ratings yet
- Thrust VectoringDocument25 pagesThrust VectoringRajgopal KakadeNo ratings yet
- BE4 Rocket EngineDocument2 pagesBE4 Rocket Enginetarx441No ratings yet
- Liquid Process Piping, Part 3 Miscellaneous Piping Design PDFDocument23 pagesLiquid Process Piping, Part 3 Miscellaneous Piping Design PDFosama alabsiNo ratings yet
- A Ballistic Missile Primer PDFDocument20 pagesA Ballistic Missile Primer PDFMartin Martin MartinNo ratings yet
- Fdocuments - in Rocket Propulsion Prof K Ramamurthi Department of Nptelacinreviewedpdfs112106073lec35pdfDocument28 pagesFdocuments - in Rocket Propulsion Prof K Ramamurthi Department of Nptelacinreviewedpdfs112106073lec35pdfKannan RamarajNo ratings yet
- Rocket TypesDocument28 pagesRocket TypesHarnil VaghasiyaNo ratings yet
- Rocket PropulsionDocument61 pagesRocket PropulsionAcsah Beth AbjNo ratings yet
- Nozzle Design Paper PDFDocument55 pagesNozzle Design Paper PDFjai_selva100% (3)
- Chemical Rocket PropulsionDocument17 pagesChemical Rocket PropulsionArpit SharmaNo ratings yet
- Deflection Check (Beams BS 8110)Document2 pagesDeflection Check (Beams BS 8110)dhanya1995No ratings yet
- Missiles Propulsion 1Document110 pagesMissiles Propulsion 1Bijin Chadayan0% (1)
- Rocketry AerodynamicsDocument56 pagesRocketry AerodynamicsHyan GontijoNo ratings yet
- OP 1157 3.5 and 5 in Aircraft Rockets 3.25 Motor 1945Document17 pagesOP 1157 3.5 and 5 in Aircraft Rockets 3.25 Motor 1945FrancescoNo ratings yet
- Pulse Detonation Engine: Nitish Kumar Regd No:-0701223318Document16 pagesPulse Detonation Engine: Nitish Kumar Regd No:-0701223318Vishal KumarNo ratings yet
- Proportional NavigationDocument5 pagesProportional NavigationD.Viswanath100% (1)
- Dynajet Pulsejet EngineDocument4 pagesDynajet Pulsejet Enginedaks4uNo ratings yet
- Active Guidance and Dynamic Flight Mechanics For Model RocketsDocument30 pagesActive Guidance and Dynamic Flight Mechanics For Model RocketsĐăng Khôi Trần100% (1)
- WarheadsDocument16 pagesWarheadsalpmal_info100% (1)
- Team Pioneer: Kevin Gu, James Leet, Amit Alon, Manpreet Singh June 7, 2012Document23 pagesTeam Pioneer: Kevin Gu, James Leet, Amit Alon, Manpreet Singh June 7, 2012aloksahu1No ratings yet
- Newsletter 346Document9 pagesNewsletter 346pete pansNo ratings yet
- Simulation and ModellingDocument10 pagesSimulation and ModellingEr Aamir Maqbool25% (4)
- Non - Metallic Denture Base MaterialsDocument15 pagesNon - Metallic Denture Base MaterialsaliNo ratings yet
- RocketDocument19 pagesRocketapi-305077843No ratings yet
- Study of Solid Rocket MotorDocument206 pagesStudy of Solid Rocket Motorapi-3827338100% (3)
- Nasa Scramjet Devlpmnt PDFDocument32 pagesNasa Scramjet Devlpmnt PDFArun Madhu100% (3)
- Pulse Detonation EngineDocument29 pagesPulse Detonation Enginev2brother100% (6)
- Kinetic Launcher For UAVDocument13 pagesKinetic Launcher For UAVLord Vario100% (1)
- Design of High Lift Low Reynolds Number Airfoil For Micro Aerial VehicleDocument7 pagesDesign of High Lift Low Reynolds Number Airfoil For Micro Aerial VehicleInternational Journal of Innovative Science and Research TechnologyNo ratings yet
- Turbin Tesla PDFDocument99 pagesTurbin Tesla PDFHaidar RahmanNo ratings yet
- Experimental Composite Propellant PDFDocument2 pagesExperimental Composite Propellant PDFLaura13% (8)
- Boundary Layer Flow over Elastic Surfaces: Compliant Surfaces and Combined Methods for Marine Vessel Drag ReductionFrom EverandBoundary Layer Flow over Elastic Surfaces: Compliant Surfaces and Combined Methods for Marine Vessel Drag ReductionNo ratings yet
- NBFC CompaniesDocument624 pagesNBFC CompaniesMithileshNo ratings yet
- NBFC CompaniesDocument624 pagesNBFC CompaniesMithileshNo ratings yet
- TOW - Tube-Launched - Optically Tracked - Wire-Guided Missle Rocket MotorDocument1 pageTOW - Tube-Launched - Optically Tracked - Wire-Guided Missle Rocket MotorhdslmnNo ratings yet
- Solid Propellant Rocket Nozzle ErosionDocument27 pagesSolid Propellant Rocket Nozzle ErosionThota Sri K Haritha100% (1)
- Model Rocket IgnitersDocument5 pagesModel Rocket IgnitersAviation/Space History LibraryNo ratings yet
- Mandrel Design For Rocket MotorsDocument4 pagesMandrel Design For Rocket Motorsobx4ever100% (1)
- Fuels in The MissilesDocument12 pagesFuels in The Missilessibi chandan100% (2)
- Catapult SystemDocument7 pagesCatapult Systemandrew munyiva0% (1)
- Scram Jet EngineDocument13 pagesScram Jet EngineRitesh80% (5)
- Theoretical and Experimental Evaluation of Pulse Jet EngineDocument59 pagesTheoretical and Experimental Evaluation of Pulse Jet EngineJonas KnollNo ratings yet
- Design and Testing of An Autorotative Payload Delivery SystemDocument11 pagesDesign and Testing of An Autorotative Payload Delivery SystemvictorNo ratings yet
- Nozzle Design Optimization To Reduce Noice For Turbo Jet EngineDocument16 pagesNozzle Design Optimization To Reduce Noice For Turbo Jet EngineSri Tech EngineeringNo ratings yet
- Chapter 15 Guidance and ControlDocument13 pagesChapter 15 Guidance and Controlramu497No ratings yet
- Bex11 Data PDFDocument1 pageBex11 Data PDFJuan Palomo (Pajarito)No ratings yet
- "Pulsejet Engine": A Project Report ONDocument35 pages"Pulsejet Engine": A Project Report ONSimran SainiNo ratings yet
- VVI Solid Rocket Motor Design and TestingDocument93 pagesVVI Solid Rocket Motor Design and Testingjai_selvaNo ratings yet
- 0010 Apx A Ordnance Descript RocketsDocument13 pages0010 Apx A Ordnance Descript RocketsChris Bass100% (2)
- Hydrogen Peroxide Gas GeneratorsDocument17 pagesHydrogen Peroxide Gas GeneratorsCliff ThriveNo ratings yet
- Fuels and New Propellants: Proceedings of the Conference Held in Milan by Federazione Associazioni Scientifiche e Tecniche and Sponsored by Consiglio Nazionale delle RicercheFrom EverandFuels and New Propellants: Proceedings of the Conference Held in Milan by Federazione Associazioni Scientifiche e Tecniche and Sponsored by Consiglio Nazionale delle RicercheCorrado CasciNo ratings yet
- TNSCERT - Basic Automobile Engineering - Thoery English Medium - 20.5.18 PDFDocument248 pagesTNSCERT - Basic Automobile Engineering - Thoery English Medium - 20.5.18 PDFjai_selvaNo ratings yet
- Finance Companies List in ChennaiDocument4 pagesFinance Companies List in Chennaijai_selva100% (1)
- List of Consultancy in Chennai Which Provide Jobs For Mechanical EngineersDocument6 pagesList of Consultancy in Chennai Which Provide Jobs For Mechanical Engineersjai_selvaNo ratings yet
- CATIA V5 Part Modeling Tutorials Useful LinksDocument2 pagesCATIA V5 Part Modeling Tutorials Useful Linksjai_selvaNo ratings yet
- Question BankDocument21 pagesQuestion Bankjai_selvaNo ratings yet
- Monthly Status Report FormatDocument3 pagesMonthly Status Report Formatjai_selvaNo ratings yet
- Tut02 MouseDocument99 pagesTut02 MouseUmut ArslanNo ratings yet
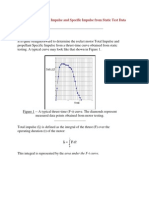
- Determining Total Impulse and Specific Impulse From Static Test DataDocument4 pagesDetermining Total Impulse and Specific Impulse From Static Test Datajai_selvaNo ratings yet
- Rocket PrincipalsDocument35 pagesRocket Principalsjai_selvaNo ratings yet
- VVI Solid Rocket Motor Design and TestingDocument93 pagesVVI Solid Rocket Motor Design and Testingjai_selvaNo ratings yet
- HDRI - High Dynamic Range ImagingDocument10 pagesHDRI - High Dynamic Range Imagingarul_mdaNo ratings yet
- CFD Analysis of Cileing Fan3 PDFDocument15 pagesCFD Analysis of Cileing Fan3 PDFsuresh kumarNo ratings yet
- Pilot Product Catalogue 18Document28 pagesPilot Product Catalogue 18veerraju tvNo ratings yet
- Practice ExamDocument6 pagesPractice ExamerjayprakashpatelNo ratings yet
- Journal of Applied Polymer Science Volume 98 Issue 2 2005 (Doi 10.1002 - App.22097) Kishore Ravi Shankar S. Sankaran - Short-Beam Three-Point Bend Tests in Syntactic Foams. Part II - Effect of MicroDocument7 pagesJournal of Applied Polymer Science Volume 98 Issue 2 2005 (Doi 10.1002 - App.22097) Kishore Ravi Shankar S. Sankaran - Short-Beam Three-Point Bend Tests in Syntactic Foams. Part II - Effect of MicroPablo OrtegaNo ratings yet
- 3074Document18 pages3074Kaushik Sengupta100% (3)
- Concentrator Photovoltaic: 13 November 2020Document23 pagesConcentrator Photovoltaic: 13 November 2020ABDUL JABBAR HASSANNo ratings yet
- Particle in An Infinite Potential BoxDocument5 pagesParticle in An Infinite Potential BoxYashmeen KaurNo ratings yet
- T3HQDocument9 pagesT3HQNkemzi Elias NzetengenleNo ratings yet
- Lab 2-Friction and Newton's Third Law InstructionsDocument2 pagesLab 2-Friction and Newton's Third Law Instructionsharinder0% (1)
- Debye ModelDocument12 pagesDebye ModelJuly T Widya RNo ratings yet
- Algae Powered Lamp by Mike ThompsonDocument19 pagesAlgae Powered Lamp by Mike ThompsonjosselinefNo ratings yet
- Fundamentals of BiomechanicsDocument11 pagesFundamentals of BiomechanicsMonwarul AzizNo ratings yet
- P2C 1200 Users Manual With OPOSDocument100 pagesP2C 1200 Users Manual With OPOSDiseño2No ratings yet
- On The Origin of The Free Radical Property of MelaninsDocument2 pagesOn The Origin of The Free Radical Property of MelaninsitbwngNo ratings yet
- Common Fourier Transforms Questions and Answers - SanfoundryDocument11 pagesCommon Fourier Transforms Questions and Answers - SanfoundrykshambelmekuyeNo ratings yet
- There Are Two Practice Activities For Unit 4.3 On Polarization. Complete Both and Attach Solutions Including WorkDocument4 pagesThere Are Two Practice Activities For Unit 4.3 On Polarization. Complete Both and Attach Solutions Including WorkBayu Adi SamodroNo ratings yet
- DnaDocument5 pagesDnaBismita SarmaNo ratings yet
- Discovery: CG4 Molecular CloudDocument2 pagesDiscovery: CG4 Molecular Cloudrpraj3135No ratings yet
- Pyrometer-Based Control of A Steam Cracking FurnaceDocument11 pagesPyrometer-Based Control of A Steam Cracking FurnaceIrfan Satrio MardaniNo ratings yet
- Sastra University: B.Tech (Eee) ProgrammeDocument14 pagesSastra University: B.Tech (Eee) ProgrammeSriram VenkatachariNo ratings yet
- 029 PDFDocument8 pages029 PDFkrishnaNo ratings yet
- Rate of Absorption of Water by Bibulous Papers: Standard Test Method ForDocument3 pagesRate of Absorption of Water by Bibulous Papers: Standard Test Method Foralucard375No ratings yet