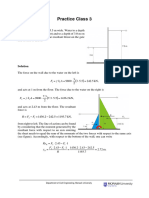
2.96 Curved panel BC is a 60 arc, perpendicular to the bottom at C.

If the panel is 4 m wide

into the paper, estimate the resultant hydrostatic force of the water on the panel.
FH   h CG A h
Solution: The horizontal force is,
 (9790 N/m3 )[2  0.5(3sin 60) m]
 [(3sin 60)m(4 m)]
 335,650 N

The vertical component equals the weight of water above the gate, which
is the sum of the rectangular piece above BC, and the curvy triangular
piece of water just above arc BC—see figure at right. (The curvy-triangle calculation is messy
and is not shown here.)

FV   (Vol)above BC  (9790 N/m 3 )[(3.0  1.133 m 2 )(4 m)]  161,860 N

The resultant force is thus,

FR  [(335,650)2  (161,860)2 ]1/2  372,635 N  373kN Ans.

This resultant force acts along a line which passes through point O at
  tan 1 (161,860/335,650)  25.7