Professional Documents
Culture Documents
PM66 fm1 PDF
PM66 fm1 PDF
Uploaded by
Gowthaman SrinivasanOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
PM66 fm1 PDF
PM66 fm1 PDF
Uploaded by
Gowthaman SrinivasanCopyright:
Available Formats
Integral Transforms for Engineers
Downloaded From: https://www.spiedigitallibrary.org/ebooks/ on 12 Aug 2020
Terms of Use: https://www.spiedigitallibrary.org/terms-of-use
Downloaded From: https://www.spiedigitallibrary.org/ebooks/ on 12 Aug 2020
Terms of Use: https://www.spiedigitallibrary.org/terms-of-use
Integral Transforms
for Engineers
Larry C. Andrews
Bhimsen K. Shivamoggi
University of Central Florida
SPIE OPTICAL ENGINEERING PRESS
A Publication of SPIE—The International Society for Optical Engineering
Bellingham, Washington USA
Downloaded From: https://www.spiedigitallibrary.org/ebooks/ on 12 Aug 2020
Terms of Use: https://www.spiedigitallibrary.org/terms-of-use
Library of Congress Cataloging-in-Publication Data
Andrews, Larry C.
Integral transforms for engineers / Larry C. Andrews, Bhimsen K. Shivamoggi
p. cm.
Originally published: New York: Macmillan, c1988.
Includes bibliographical references and index.
ISBN 0-8194-3232-6
1. Shivamoggi, Bhimsen K. II. Title.
QA432.A63 1999
515'.723—dc21 99-14143
CIP
Published by
SPIE—The International Society for Optical Engineering
P.O. Box 10
Bellingham, Washington 98227-0010
Phone: 360/676-3290
Fax: 360/647-1445
E-mail: spie @spie.org
WWW: http://www.spie.org/
Copyright © 1999 The Society of Photo-Optical Instrumentation Engineers
(Originally published in 1988 by Macmillan Publishing Company, New York.)
All rights reserved. No part of this publication may be reproduced or distributed
in any form or by any means without written permission of the publisher.
Printed in the United States of America.
Downloaded From: https://www.spiedigitallibrary.org/ebooks/ on 12 Aug 2020
Terms of Use: https://www.spiedigitallibrary.org/terms-of-use
Contents
Preface to the 1999 Printing vii
Preface ix
Introduction 1
1 SPECIAL FUNCTIONS 6
1.1 Introduction 6
1.2 The Gamma Function 7
1.3 The Error Function and Related Functions 16
1.4 Bessel Functions 21
1.5 Useful Engineering Functions 29
2 FOURIER INTEGRALS AND FOURIER TRANSFORMS 37
2.1 Introduction 37
2.2 Fourier Integral Representations 38
2.3 Proof of the Fourier Integral Theorem 47
2.4 Fourier Transform Pairs 49
2.5 Properties of the Fourier Transform 58
2.6 Transforms of More Complicated Functions 65
2.7 The Convolution Integrals of Fourier 78
2.8 Transforms Involving Generalized Functions 85
2.9 Hilbert Transforms 91
2.10 Additional Topics 97
3 APPLICATIONS INVOLVING FOURIER TRANSFORMS 102
3.1 Introduction 102
3.2 Boundary Value Problems 103
3.3 Heat Conduction in Solids 113
3.4 Mechanical Vibrations 125
3.5 Potential Theory 131
3.6 Hydrodynamics 141
3.7 Elasticity in Two Dimensions 151
3.8 Probability and Statistics 156
4 THE LAPLACE TRANSFORM 162
4.1 Introduction 162
4.2 The Transforms of Some Typical Functions 164
V
Downloaded From: https://www.spiedigitallibrary.org/ebooks/ on 12 Aug 2020
Terms of Use: https://www.spiedigitallibrary.org/terms-of-use
vi Contents
4.3 Basic Operational Properties 170
4.4 Transforms of More Complicated Functions 182
4.5 The Inverse Laplace Transform 190
4.6 Complex Inversion Formula 200
4.7 Additional Topics 210
5 APPLICATIONS INVOLVING LAPLACE TRANSFORMS 218
5.1 Introduction 218
5.2 Evaluating Integrals 218
5.3 Solutions of ODEs 221
5.4 Solutions of PDEs 229
5.5 Linear Integral Equations 238
6 THE MELLIN TRANSFORM 245
6.1 Introduction 245
6.2 Evaluation of Mellin Transforms 246
6,3 Complex Variable Methods 254
6.4 Applications 262
6.5 Table of Mellin Transforms 273
7 THE HANKEL TRANSFORM 274
7.1 Introduction 274
7.2 Evaluation of Hankel Transforms 276
7.3 Applications 285
7.4 Table of Hankel Transforms 290
8 FINITE TRANSFORMS 291
8.1 Introduction 291
8.2 Finite Fourier Transforms 291
8.3 Sturm—Liouville Transforms 298
8.4 Finite Hankel Transform 303
9 DISCRETE TRANSFORMS 310
9.1 Introduction 310
9.2 Discrete Fourier Transform 311
9.3 The Z Transform 321
9.4 Difference Equations 330
9.5 Table of Z Transforms 333
BIBLIOGRAPHY 335
APPENDIX A: REVIEW OF COMPLEX VARIABLES 337
APPENDIX B: TABLE OF FOURIER TRANSFORMS 340
APPENDIX C: TABLE OF LAPLACE TRANSFORMS 344
INDEX 349
Downloaded From: https://www.spiedigitallibrary.org/ebooks/ on 12 Aug 2020
Terms of Use: https://www.spiedigitallibrary.org/terms-of-use
Preface to the 1999 Printing
The use of Fourier integrals in mathematics and physics applications dates back
to the pioneering work of Joseph Fourier (1768-1830). Since that time, the
notion of the integral transform has emerged as a related tool that owes much
of its success to the work of Oliver Heaviside (1850-1925), an English
electrical engineer who popularized the use of operational methods in
differential equations and electrical engineering. During the last decade or so
there have been significant generalizations of the idea of integral transforms
and many new uses of the transform method in engineering and physics
applications. Some of these new applications have prompted the development
of very specialized transforms, such as the wavelet transform, that have their
roots, however, deeply entrenched in the classical theory of Fourier. As a
result, knowledge of the properties and use of classical integral transforms,
such as the Fourier transform and Laplace transform, are just as important
today as they have been for the last century or so.
This text was written in 1988 as an introductory treatment of integral
transforms for practicing engineers and scientists, including the Fourier,
Laplace, Mellin, Hankel, finite, and discrete transforms. Like the fate of many
modem textbooks, the original publishing company changed hands and this
book went out of print after a few years. Nonetheless, a number of individuals
took the time to let us know they found the book useful as either a personal
reference text or as a classroom text, and also expressed their disappointment
in seeing it go out of print. We are therefore grateful to the SPIE PRESS for
agreeing to bring the book back into print. As authors, we have taken this
opportunity to correct several typographical errors that appeared in the first
printing, but would welcome hearing from anyone who finds additional
typographical errors that we did not catch or who cares to give any suggestions
for further improvements as well.
Larry C. Andrews
Bhimsen K. Shivamoggi
Orlando, Florida
March, 1999
VII
Downloaded From: https://www.spiedigitallibrary.org/ebooks/ on 12 Aug 2020
Terms of Use: https://www.spiedigitallibrary.org/terms-of-use
Downloaded From: https://www.spiedigitallibrary.org/ebooks/ on 12 Aug 2020
Terms of Use: https://www.spiedigitallibrary.org/terms-of-use
Preface
IN RECENT YEARS, INTEGRAL TRANSFORMS have become essential working
tools of every engineer and applied scientist. The Laplace transform,
which undoubtedly is the most familiar example, is basic to the solution
of initial value problems. The Fourier transform, while being suited to
solving boundary-value problems, is basic to the frequency spectrum
analysis of time-varying waveforms. The purpose of this text is to introduce
the use of integral transforms in obtaining solutions to problems governed
by ordinary and partial differential equations and certain types of integral
equations. Some other applications are also covered where appropriate.
The Laplace and Fourier transforms are by far the most widely used
of all integral transforms. For this reason they have been given a more
extensive treatment in this book than other integral transforms. However,
there are several other integral transforms that also have been used
successfully in the solution of certain boundary-value problems and in
other applications. Included in this category are Mellin, Hankel, finite,
and discrete transforms, which have also been given some discussion
here.
The text is directed primarily toward senior and beginning graduate
students in engineering sciences, physics, and mathematics who desire
a deeper knowledge of transform methods than can be obtained in in-
troductory courses in differential equations and other similar courses. It
can also be used as a self-study text for practicing engineers and applied
scientists who wish to learn more about the general theory and use of
integral transforms. We assume the reader has a basic knowledge of
ix
Downloaded From: https://www.spiedigitallibrary.org/ebooks/ on 12 Aug 2020
Terms of Use: https://www.spiedigitallibrary.org/terms-of-use
. Preface
differential equations and contour integration techniques from complex
variables. However, most of the material involving complex variables
occurs in separate sections so that much of the text can be accessible
to those with a minimum background in complex variable methods. As
an aid in this regard, we have included a brief appendix relevant to our
use of the basic concepts and theory of complex variables in the text.
Also, because of the close association of special functions and integral
transforms, the first chapter is a short introduction to several of the
special functions that arise quite frequently in applications. This is con-
sidered an optional chapter for those with some acquaintance with these
functions, and thus it is possible to start the text with Chap. 2. Most
chapters are independent of one another so that various arrangements
of the material are possible.
Applications occur throughout the text and are drawn from the fields
of mechanical vibration, heat conduction, potential theory, mechanics
of solids and fluids, probability and statistics, and several other areas.
A working knowledge in any of these areas is generally sufficient to work
the examples and exercises.
In our treatment of integral transforms we have excised formal proofs
in several places, but then usually make an appropriate reference for the
more formal aspects of the theory. In the applications we often make
the assumptions as to the commutability of certain limiting operations,
and the derivation of a particular solution sometimes may not be rigorous.
However, the approach adopted here is adequate in the usual applications
in engineering and applied sciences. We have included a large number
of worked examples and exercises to illustrate the versatility and adequacy
of this approach in applications to physical problems.
We wish to thank Jack Repcheck, Senior Editor of Scientific and
Technical Books department at Macmillan, for his assistance in getting
this text published in a timely manner. We also wish to express our
appreciation to the production staff of Macmillan for their fine efforts.
Finally, we wish to acknowledge Martin Otte who corrected several
errors during a final reading of the manuscript.
Downloaded From: https://www.spiedigitallibrary.org/ebooks/ on 12 Aug 2020
Terms of Use: https://www.spiedigitallibrary.org/terms-of-use
Introduction
The classical methods of solution of initial and boundary value problems
in physics and engineering sciences have their roots in Fourier's pioneering
work. An alternative approach through integral transform methods emerged
primarily through Heaviside's efforts on operational techniques. In addition
to being of great theoretical interest to mathematicians, integral transform
methods have been found to provide easy and effective ways of solving
a variety of problems arising in engineering and physical science. The
use of an integral transform is somewhat analogous to that of logarithms.
That is, a problem involving multiplication or division can be reduced
to one involving the simpler processes of addition or subtraction by taking
logarithms. After the solution has been obtained in the logarithm domain,
the original solution can be recovered by finding an antilogarithm. In the
same way, a problem involving derivatives can be reduced to a simpler
problem involving only multiplication by polynomials in the transform
variable by taking an integral transform, solving the problem in the
transform domain, and then finding an inverse transform. Integral trans-
forms arise in a natural way through the principle of linear superposition
in constructing integral representations of solutions of linear differential
equations.
Downloaded From: https://www.spiedigitallibrary.org/ebooks/ on 12 Aug 2020
Terms of Use: https://www.spiedigitallibrary.org/terms-of-use
2 • Introduction
By an integral transform, we mean a relation of the form*
I K(s, t)f(t) dt = F(s) (0.1)
such that a given function f(t) is transformed into another function F(s)
by means of an integral. The new function F(s) is said to be the transform
of f(t), and K(s,t) is called the kernel of the transformation. Both
K(s, t) and f(t) must satisfy certain conditions to ensure existence of the
integral and a unique transform function F(s). Also, generally speaking,
not more than one function f(t) should yield the same transform F(s).
When both of the limits of integration in the defining integral are finite,
we have what is called a finite transform.
Within the above guidelines there are a variety of kernels that may
be used to define particular integral transforms for a wide class of functions
f(t). If the kernel is defined by
K(s, t) = j 0 '-sr, t ^ 0 (0.2)
the resulting transform
e S`f(t) dt = F(s) (0.3)
fo -
-
is called the Laplace transform. When
K(s, t) __ 1 e`" (0.4)
we generate the Fourier transformt
2 - J e sc f(t) dt = F(s) (0.5)
which, when t is restricted to the positive real line, leads to the Fourier
sine and Fourier cosine transforms
_/ ƒ — ƒ(t)sin st dt = F(s) (0.6)
We will always interpret integrals like (0.1) as the principal value of the integral,
Jim
defined in general by PV j x f(x)dx = jN f(x)dx.
R . - N
t Other definitions of K(s,t) for Fourier transforms involve the choices e", e",
(l/2ir)e", among others.
Downloaded From: https://www.spiedigitallibrary.org/ebooks/ on 12 Aug 2020
Terms of Use: https://www.spiedigitallibrary.org/terms-of-use
Introduction • 3
and
^2 ƒ o ƒ(t)cos st dt = F(s)
— (0.7)
The Laplace and Fourier transforms are by far the most prominent
in applications. Many other transforms have been developed, but most
have limited applicability. In addition to the Laplace and Fourier transforms,
the next most useful transforms are perhaps the Hankel transform of
order v
f tJ,(st)f(t) dt = F(s) (0.8)
where J„(x) is the Bessel function of the first kind (see Sec. 1.4), and
the Mellin transform
fo— ts `f(t) dt = F(s)
- (0.9)
The Hankel transform arises naturally in solving boundary value problems
formulated in cylindrical coordinates while the Mellin transform is useful
in the solution of certain potential problems formulated in wedge-shaped
regions.
The integral transforms mentioned thus far are applicable to problems
involving either semiinfinite or infinite domains. However, in applying
the method of integral transforms to problems formulated on finite domains
it is necessary to introduce finite intervals on the transform integral.
Transforms of this nature are called finite integral transforms.
A basic problem in the use of integral transforms is to determine the
function f(t) when its transform F(s) is known. We refer to this as the
inverse problem. In many cases the solution of the inverse problem is
another integral transform relation of the type
f H(s, t)F(s) ds = f(t)
D (0.10)
where H(s, t) is another kernel and D is the domain of s. Such a result
is called an inversion formula for the particular transform. For example,
the inversion formula for the Fourier transform takes the form (see Sec.
2.4)
ç 2^ I e 'S`F(s) ds = f(t) (0.11)
which is very much like the transform itself in Eq. (0.5). This means
that the problems of evaluating transforms or inverse transforms are
Downloaded From: https://www.spiedigitallibrary.org/ebooks/ on 12 Aug 2020
Terms of Use: https://www.spiedigitallibrary.org/terms-of-use
4 . Introduction
essentially the same for Fourier transforms. This is not necessarily the
case for other transforms like the Laplace transform, however, where
the inversion formula is quite distinct from that of the transform integral.
Also, in the case of finite transforms, the inverse transform is in the
form of an infinite series.
The basic aim of the transform method is to transform a given problem
into one that is easier to solve. In the case of an ordinary differential
equation with constant coefficients, the transformed problem is algebraic.
The effect of applying an integral transform to a partial differential equation
is to reduce it to a partial differential equation in one less variable. The
solution of the transformed problem in either case will be a function of
the transformed variable and any remaining independent variables. In-
version of this solution produces the solution of the original problem.
The exponential Fourier transform does not incorporate any boundary
conditions in transforming the derivatives. Thus, it is best suited for
solving differential equations on infinite domains where the boundary
conditions usually only require bounded solutions. On the other hand,
the Fourier cosine and sine transforms are well suited for solving certain
problems on semiinfinite domains where the governing differential equation
involves only even-order derivatives. We will see that the Fourier transform
lends itself nicely to solving boundary-value problems associated with
the following partial differential equations:
(a)the heat equation:
V 2 u = a -2 U t — q(x,y,z,t) (0.12)
(b)the wave equation:
V 2 u = c -Zu rr — q(x,y,z,t) (0.13)
(c) the potential equation:
V2u = 0 (0.14)
In addition, it is useful in the solution of linear integral equations of the
form
f(x) = u(x) — A 1 — k(x, t)u(t) dt (0.15)
and certain ordinary differential equations. Interesting applications of
these transform methods arise in hydrodynamics, heat conduction, potential
theory, and elasticity theory, among other areas. The Fourier transform
also lends itself to the theory of probability and statistics. For example,
it turns out that the moments of a random variable X are merely the
coefficients of (it)"/k! in the Maclaurin series expansion of the characteristic
function C(t) of the random variable X, and this function is related to
Downloaded From: https://www.spiedigitallibrary.org/ebooks/ on 12 Aug 2020
Terms of Use: https://www.spiedigitallibrary.org/terms-of-use
Introduction • 5
the probability density function p(x) by the Fourier transform relation
C(t) = I ^e"X p(x) dx (0.16)
While the Fourier transform is suited for boundary-value problems,
the Laplace transform is suited for initial-value problems. However, there
are other situations for which the Laplace transform can also be used,
such as in the evaluation of certain integrals and in the solution of certain
integral equations of convolution type like
(0.17)
ƒo u(T)k(t — r) dr f(t),
t
t> 0
In addition to the transforms mentioned above, there are other less
well known transforms like the Hilbert transform and the Sturm—Liouville
transform, both of which are more limited in their usefulness than the
Fourier and Laplace transforms. Also, discrete transforms like the discrete
Fourier transform (which is the discrete analog of the Fourier transform)
and the Z transform (which is the discrete analog of the Laplace transform)
are becoming more prominent in various engineering applications where
it is either impossible or inconvenient to use more conventional transforms.
Much of our initial discussion will evolve around the problem of
calculating the transforms F(s) of given functions f(t), and also around
the related problem of finding inverse transforms of various functions
F(s). Our primary objective is to introduce methods to use the integral
transforms, rather than concerning ourselves too deeply with the general
theory itself. Therefore, we do not attempt to present the basic theorems
in their most general forms. However, the conditions put forth in the
theorems are generally broad enough to embrace most of the functions
that naturally arise in engineering and physical situations: Proofs of the
theorems are provided when feasible, but are sometimes based on heuristic
arguments instead of rigorous mathematical procedures. For example,
often we have the need in our proofs for interchanging certain limit
operations, like integration and summation, and in these situations we
normally operate under the assumption that such interchanges are
permissible.
Downloaded From: https://www.spiedigitallibrary.org/ebooks/ on 12 Aug 2020
Terms of Use: https://www.spiedigitallibrary.org/terms-of-use
You might also like
- Textbook Ebook Applied Mechanics of Polymers Properties Processing and Behavior George Youssef All Chapter PDFDocument43 pagesTextbook Ebook Applied Mechanics of Polymers Properties Processing and Behavior George Youssef All Chapter PDFbetty.combs185100% (6)
- Lectures On The Fourier Transform and Its Applications: SallyDocument713 pagesLectures On The Fourier Transform and Its Applications: Sallyvic1234059No ratings yet
- Multiphysics Modeling: Numerical Methods and Engineering Applications: Tsinghua University Press Computational Mechanics SeriesFrom EverandMultiphysics Modeling: Numerical Methods and Engineering Applications: Tsinghua University Press Computational Mechanics SeriesRating: 5 out of 5 stars5/5 (1)
- Fundamentals Of Solar Cells: Photovoltaic Solar Energy ConversionFrom EverandFundamentals Of Solar Cells: Photovoltaic Solar Energy ConversionNo ratings yet
- Wasyl Wasylkiwskyj (Auth.) - Signals and Transforms in Linear Systems Analysis-Springer-Verlag New York (2013) PDFDocument387 pagesWasyl Wasylkiwskyj (Auth.) - Signals and Transforms in Linear Systems Analysis-Springer-Verlag New York (2013) PDFPasupuleti SivakumarNo ratings yet
- Business Mathematics AssignmentDocument5 pagesBusiness Mathematics Assignmentanish1012No ratings yet
- Balint Training System 1948Document16 pagesBalint Training System 1948Laura Acosta100% (2)
- Math140 Final 2010fDocument10 pagesMath140 Final 2010fexamkillerNo ratings yet
- Integral Transforms For EngineersDocument365 pagesIntegral Transforms For EngineersSouvik PaulNo ratings yet
- PDF An Invitation To Applied Category Theory Seven Sketches in Compositionality 1St Edition Brendan Fong Ebook Full ChapterDocument54 pagesPDF An Invitation To Applied Category Theory Seven Sketches in Compositionality 1St Edition Brendan Fong Ebook Full Chapterjames.fahey314100% (5)
- Preview-9781108515658 A30632538Document55 pagesPreview-9781108515658 A30632538abolfazlesmaeiliaeNo ratings yet
- Martin Goosey (Auth.), Martin Goosey (Eds.) - Plastics For Electronics-Springer Netherlands (1999)Document408 pagesMartin Goosey (Auth.), Martin Goosey (Eds.) - Plastics For Electronics-Springer Netherlands (1999)totyNo ratings yet
- Indifference Pricing: Theory and ApplicationsFrom EverandIndifference Pricing: Theory and ApplicationsRating: 3 out of 5 stars3/5 (1)
- Vacuum MicroelectronicsFrom EverandVacuum MicroelectronicsWei ZhuNo ratings yet
- Use of Laser in HighwayDocument29 pagesUse of Laser in HighwayAKASH KUMAR50% (2)
- HydraulicsDocument231 pagesHydraulicsKristijan HorvatNo ratings yet
- Design of Gas Bearing Systems For Precision Applications: WWW - Tue.nl/taverneDocument152 pagesDesign of Gas Bearing Systems For Precision Applications: WWW - Tue.nl/taverneGiovanniNo ratings yet
- Solar Based Smart Industrial Automation System - BookDocument72 pagesSolar Based Smart Industrial Automation System - BookRakibul HassanNo ratings yet
- CFD Analysis of Flue Gas Duct OF 500Mw Pulverised Coal BoilerDocument6 pagesCFD Analysis of Flue Gas Duct OF 500Mw Pulverised Coal BoilerjaveddvcNo ratings yet
- Chapter 1 Overview of Project 1-3Document3 pagesChapter 1 Overview of Project 1-3GALAXYNo ratings yet
- Ebook Calculus Set Free Infinitesimals To The Rescue 1St Edition C Bryan Dawson Online PDF All ChapterDocument69 pagesEbook Calculus Set Free Infinitesimals To The Rescue 1St Edition C Bryan Dawson Online PDF All Chapterraymond.hefferman768100% (8)
- Ebook Radial Flow Turbocompressors Design Analysis and Applications 1St Edition Casey Online PDF All ChapterDocument69 pagesEbook Radial Flow Turbocompressors Design Analysis and Applications 1St Edition Casey Online PDF All Chapterhelen.martin283100% (7)
- PDF Fundamentals of Graphics Using Matlab 1St Edition Ranjan Parekh Ebook Full ChapterDocument53 pagesPDF Fundamentals of Graphics Using Matlab 1St Edition Ranjan Parekh Ebook Full Chaptermichael.legore799100% (2)
- (Download PDF) Foundations of Software Engineering Ashfaque Ahmed Online Ebook All Chapter PDFDocument36 pages(Download PDF) Foundations of Software Engineering Ashfaque Ahmed Online Ebook All Chapter PDFnancy.cooper309100% (10)
- PP IDCbookextract R15Document28 pagesPP IDCbookextract R15gocoolonNo ratings yet
- Large Scale Linear and Integer Optimization: A Unified ApproachDocument739 pagesLarge Scale Linear and Integer Optimization: A Unified Approachpofibig689No ratings yet
- Duality and Modern Economics - Cornes PDFDocument304 pagesDuality and Modern Economics - Cornes PDFAustin S. HooeNo ratings yet
- Statistical Rethinking A Bayesian Course With Examples in R and STAN Chapman Hall CRC Texts in Statistical Science Richard McelreathDocument43 pagesStatistical Rethinking A Bayesian Course With Examples in R and STAN Chapman Hall CRC Texts in Statistical Science Richard Mcelreathedward.furstenberg353100% (8)
- FYP Dissertation Report (FINAL)Document49 pagesFYP Dissertation Report (FINAL)Jerick De VeraNo ratings yet
- Modeling and Simulation of Mineral Processing SystemsFrom EverandModeling and Simulation of Mineral Processing SystemsRating: 5 out of 5 stars5/5 (1)
- Helical Piles A Practical Guide To Design and Installation Part1 PDFDocument512 pagesHelical Piles A Practical Guide To Design and Installation Part1 PDFRalitsa OlevaNo ratings yet
- Robotics: Designing the Mechanisms for Automated MachineryFrom EverandRobotics: Designing the Mechanisms for Automated MachineryRating: 4.5 out of 5 stars4.5/5 (8)
- Advanced AM HandbookDocument290 pagesAdvanced AM HandbookBikash ChoudhuriNo ratings yet
- Genius Plus Ba Cu en 1113Document72 pagesGenius Plus Ba Cu en 1113Supriyanto yantoNo ratings yet
- (Download PDF) Practical Foundations For Programming Languages 2Nd Edition Robert Harper Online Ebook All Chapter PDFDocument42 pages(Download PDF) Practical Foundations For Programming Languages 2Nd Edition Robert Harper Online Ebook All Chapter PDFrichard.blanchard477100% (9)
- ContentsDocument2 pagesContentsNaveen YallapuNo ratings yet
- 12 P 2Document230 pages12 P 2api-3812386100% (1)
- Manual Rexroth RE15215Document64 pagesManual Rexroth RE15215Comassur SA de CV100% (1)
- U of Sheffield: The DiversityDocument270 pagesU of Sheffield: The DiversityBrata PatandeanNo ratings yet
- Uday Vaidya 654141576 PDFDocument5 pagesUday Vaidya 654141576 PDFVictor Daniel WaasNo ratings yet
- Analytic Number Theory For Beginners 2Nd Edition Prapanpong Pongsriiam Online Ebook Texxtbook Full Chapter PDFDocument69 pagesAnalytic Number Theory For Beginners 2Nd Edition Prapanpong Pongsriiam Online Ebook Texxtbook Full Chapter PDFcarmen.doe585100% (15)
- Ebook The Logic of Capital An Introduction To Marxist Economic Theory 1St Edition Deepankar Basu Online PDF All ChapterDocument69 pagesEbook The Logic of Capital An Introduction To Marxist Economic Theory 1St Edition Deepankar Basu Online PDF All Chapteredythe.barr970100% (8)
- Get ItDocument40 pagesGet ItShubham NarvekarNo ratings yet
- Final Year Project ReportDocument75 pagesFinal Year Project ReportShaikNo ratings yet
- Designing Indoor Solar Products: Photovoltaic Technologies for AESFrom EverandDesigning Indoor Solar Products: Photovoltaic Technologies for AESNo ratings yet
- HRSG Lifing BriefDocument12 pagesHRSG Lifing BriefAnonymous utxGVB5Vy100% (1)
- 3e 2016 1206789 1Document82 pages3e 2016 1206789 1temesgen tesemaNo ratings yet
- Textbook Materials and Water Chemistry For Supercritical Water Cooled Reactors 1St Edition David Guzonas Ebook All Chapter PDFDocument53 pagesTextbook Materials and Water Chemistry For Supercritical Water Cooled Reactors 1St Edition David Guzonas Ebook All Chapter PDFgeorge.storey958100% (10)
- Flower1995 Book HighPerformanceMaterialsInAeroDocument393 pagesFlower1995 Book HighPerformanceMaterialsInAeroau00843929100% (1)
- I2985 1.0en GEN2i User ManualDocument146 pagesI2985 1.0en GEN2i User ManualRoberto OvandoNo ratings yet
- C. Bryan Dawson - Calculus Set Free - Infinitesimals To The Rescue-Oxford University Press (2022)Document1,617 pagesC. Bryan Dawson - Calculus Set Free - Infinitesimals To The Rescue-Oxford University Press (2022)hopoha100% (1)
- Task 5 Lot 6 Ventilation Final ReportDocument64 pagesTask 5 Lot 6 Ventilation Final ReportDigvijay Singh100% (1)
- Manual Epsilon 12v100ah 12v150ah v1-7 enDocument38 pagesManual Epsilon 12v100ah 12v150ah v1-7 endavidfernandoariascruz685No ratings yet
- Report 2022Document17 pagesReport 2022Rita MarrounNo ratings yet
- P 0456 Automatic Solar Rad TrackerDocument95 pagesP 0456 Automatic Solar Rad TrackerSam Mathew100% (1)
- The Evaluation of Time Claims in Construction ProjectsDocument407 pagesThe Evaluation of Time Claims in Construction ProjectsmarkNo ratings yet
- Mathematical Techniques For Engineers and Scientists (PDFDrive)Document816 pagesMathematical Techniques For Engineers and Scientists (PDFDrive)Charlie E RobledoNo ratings yet
- Power Plant Equipment Operation and Maintenance Guide: Maximizing Efficiency and ProfitabilityDocument17 pagesPower Plant Equipment Operation and Maintenance Guide: Maximizing Efficiency and ProfitabilityMaterials Engineer100% (2)
- Full Download Book Practical Guide To Rotational Moulding PDFDocument41 pagesFull Download Book Practical Guide To Rotational Moulding PDFmark.king621100% (23)
- "A S F D A D ": Inguistic IGN OmmunicatorDocument56 pages"A S F D A D ": Inguistic IGN OmmunicatorResearch PaperNo ratings yet
- Handbook of Corrosion Engineering: Pierre R. RobergeDocument9 pagesHandbook of Corrosion Engineering: Pierre R. RobergemarboledtNo ratings yet
- Textbook Modeling of Chemical Wear Relevance To Practice 1St Edition A Sethuramiah Ebook All Chapter PDFDocument53 pagesTextbook Modeling of Chemical Wear Relevance To Practice 1St Edition A Sethuramiah Ebook All Chapter PDFkimberly.edmunds190100% (9)
- (Tutorial Guides in ElectronicEngineering-Springer US (1994) 6Document1 page(Tutorial Guides in ElectronicEngineering-Springer US (1994) 6Pasupuleti SivakumarNo ratings yet
- (Tutorial Guides in ElectronicEngineering-Springer US (1994) 5Document1 page(Tutorial Guides in ElectronicEngineering-Springer US (1994) 5Pasupuleti SivakumarNo ratings yet
- Power Electronics-3rd ChapterDocument80 pagesPower Electronics-3rd ChapterPasupuleti SivakumarNo ratings yet
- Power Electronics-1st ChapterDocument24 pagesPower Electronics-1st ChapterPasupuleti SivakumarNo ratings yet
- Power Electronics Contents by Issa BatarsehDocument5 pagesPower Electronics Contents by Issa BatarsehPasupuleti SivakumarNo ratings yet
- Vehicle Electrical System - MATLAB & Simulink Example - MathWorks IndiaDocument2 pagesVehicle Electrical System - MATLAB & Simulink Example - MathWorks IndiaPasupuleti SivakumarNo ratings yet
- IntegrationDocument6 pagesIntegrationPasupuleti SivakumarNo ratings yet
- Motor Torque Calculations For Electric Vehicle PDFDocument2 pagesMotor Torque Calculations For Electric Vehicle PDFPasupuleti SivakumarNo ratings yet
- Time Scope Measurements - MATLAB & Simulink Example - MathWorks IndiaDocument8 pagesTime Scope Measurements - MATLAB & Simulink Example - MathWorks IndiaPasupuleti SivakumarNo ratings yet
- Windows 10 Product Key Free For You - Apps For WindowsDocument5 pagesWindows 10 Product Key Free For You - Apps For WindowsPasupuleti Sivakumar100% (1)
- Block Inputs and Outputs: MultimeterDocument1 pageBlock Inputs and Outputs: MultimeterPasupuleti SivakumarNo ratings yet
- Modeling of A Hybrid Electric Vehicle Powertrain Test Cell Using Bond GraphsDocument9 pagesModeling of A Hybrid Electric Vehicle Powertrain Test Cell Using Bond GraphsPasupuleti SivakumarNo ratings yet
- Converters and DC Bus Tab: e D DT R R MDocument1 pageConverters and DC Bus Tab: e D DT R R MPasupuleti SivakumarNo ratings yet
- RemarksDocument1 pageRemarksPasupuleti SivakumarNo ratings yet
- 1 PDFDocument1 page1 PDFPasupuleti SivakumarNo ratings yet
- PI Controller Based Torque and Speed Control of Five Phase Switched Reluctance MotorDocument6 pagesPI Controller Based Torque and Speed Control of Five Phase Switched Reluctance MotorPasupuleti SivakumarNo ratings yet
- Dialog Box: Asynchronous Machine TabDocument1 pageDialog Box: Asynchronous Machine TabPasupuleti SivakumarNo ratings yet
- Space Vector PWM VSI Induction Motor Drive: LibraryDocument1 pageSpace Vector PWM VSI Induction Motor Drive: LibraryPasupuleti SivakumarNo ratings yet
- AS Integration I AssessmentDocument2 pagesAS Integration I AssessmentAbd Elrhman MohamedNo ratings yet
- Chemistry: Acid - Base Titration Analysis Using Antacid TabletDocument10 pagesChemistry: Acid - Base Titration Analysis Using Antacid TabletjaninasuzetteNo ratings yet
- Introduction To Focus GroupDocument6 pagesIntroduction To Focus GroupNur HayaniNo ratings yet
- Bachelor of Arts in Communicative Thai Language For Foreigners (International Program)Document18 pagesBachelor of Arts in Communicative Thai Language For Foreigners (International Program)Adha Estu RizqiNo ratings yet
- H2 Maths Weekend Assignment For JC2: 2009 JJC Prelim Exam P 1Document4 pagesH2 Maths Weekend Assignment For JC2: 2009 JJC Prelim Exam P 1ManFang NeoNo ratings yet
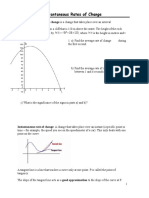
- 1 11 Instantaneous Rate of Change Note and HWDocument5 pages1 11 Instantaneous Rate of Change Note and HWSyed Saad HussainNo ratings yet
- Assignment 1Document10 pagesAssignment 1eXcuvatorNo ratings yet
- Module 5Document10 pagesModule 5Hanely De La PeñaNo ratings yet
- Volume of Revolution WorksheetDocument4 pagesVolume of Revolution Worksheetwanlilyaisyah1378No ratings yet
- Examples and Exercises - Module 3Document6 pagesExamples and Exercises - Module 3Favour Nmesoma NwaforNo ratings yet
- Moving AverageDocument12 pagesMoving AveragesanjaydrdoNo ratings yet
- Experiment 1 Potentiometric Titration: Joan Marie Ilagan Joanne Sasondoncillo Ma. Kezia TayagDocument11 pagesExperiment 1 Potentiometric Titration: Joan Marie Ilagan Joanne Sasondoncillo Ma. Kezia Tayagjoai_11No ratings yet
- Big M MethodDocument4 pagesBig M MethodChui PhinNo ratings yet
- StatProb Monthly Exam 2022 2023Document3 pagesStatProb Monthly Exam 2022 2023Marc AguinaldoNo ratings yet
- Asset-V1 MITx+6.86x+3T2020+typeasset+blockslides Lecture4 CompressedDocument22 pagesAsset-V1 MITx+6.86x+3T2020+typeasset+blockslides Lecture4 CompressedRahul VasanthNo ratings yet
- CollectionDocument4 pagesCollectionAhuja AbhishekNo ratings yet
- Statistics Formulae For FoundationDocument7 pagesStatistics Formulae For Foundationanon_127497276100% (1)
- Analisis Kafein, Taurin, Dan Pemanis BuatanDocument9 pagesAnalisis Kafein, Taurin, Dan Pemanis BuatanneaNo ratings yet
- Research Methods in Health Investigating Health An... - (Research Methods in Health Investigating Health and Health Services)Document10 pagesResearch Methods in Health Investigating Health An... - (Research Methods in Health Investigating Health and Health Services)Natassa FerentinouNo ratings yet
- Analytical Chemistry: Volumetric Analysis)Document21 pagesAnalytical Chemistry: Volumetric Analysis)Bryar HusenNo ratings yet
- Eigenfunctions of Discrete Time LTI SystemsDocument2 pagesEigenfunctions of Discrete Time LTI SystemsKrsto ProrokovicNo ratings yet
- Lecture 23 - Parallel Transport (Schuller's Geometric Anatomy of Theoretical Physics)Document6 pagesLecture 23 - Parallel Transport (Schuller's Geometric Anatomy of Theoretical Physics)Simon ReaNo ratings yet
- MS 1 - 3 ReportDocument19 pagesMS 1 - 3 ReportNauman Mithani100% (1)
- Group3 AssigmtDocument3 pagesGroup3 AssigmtHafiz Bin HarunNo ratings yet
- Vector Tensor CalculusDocument300 pagesVector Tensor CalculusDiogo Martins100% (3)
- Math PDFDocument120 pagesMath PDFAshwin KoradeNo ratings yet
- Quasi-Periodic Solutions Calculated With The Simple Shooting TechniqueDocument12 pagesQuasi-Periodic Solutions Calculated With The Simple Shooting TechniqueLạc DươngNo ratings yet