INTERNATIONAL JOURNAL OF CIVIL AND STRUCTURAL ENGINEERING

Volume 3, No 3, 2013
© Copyright by the authors - Licensee IPA- Under Creative Commons license 3.0
Research article ISSN 0976 – 4399

Dynamic analysis of T-Beam bridge superstructure

Supriya Madda1, Kalyanshetti M.G2
1- Post graduate student, Walchand Institute of Technology,Solapur, India.
2- Assistant Professor, Civil Engineering Department, Walchand Institute of Technology,
Solapur, India.
supriya.madda@gmail.com
doi:10.6088/ijcser.201203013045

ABSTRACT

Generally, structures are subjected to two types of load: static and dynamic. However, the
majority of civil engineering structures are designed with the assumption that all applied
loads are static. The effect of dynamic load is not considered because the structure is rarely
subjected to dynamic loads; more so, its consideration in analysis makes the solution more
complicated and time consuming. This feature of neglecting the dynamic forces may
sometimes become the cause of disaster, particularly in the case of earthquake. Nowadays,
there is a growing interest in the process of designing structures capable to withstand
dynamic loads, particularly, earthquake-induced load. This is needed to be done, because, in
present scenario where earthquakes are occurring frequently, dynamic force cannot be
neglected. Therefore it is proposed to do “dynamic analysis of bridge deck” for various span
of bridge by varying no. of longitudinal girders. The detailed study is carried out for “T-
Beam Bridge”, for two lane and four lane of spans 15m, 20m, 25m, 30m, 35m using IRC
class A loading. For analysis SAP2000 software is used. Finally, to envelope the
serviceability, the bridge responses are obtained.

Keyword: Longitudinal girder, dynamic analysis, T-beam bridge, SAP2000, IRC class A.

1. Introduction

For ordinary structures, static analysis is sufficient but for important structures particularly
for bridges, dynamic analysis needs to be carried out. Because, it provides an accurate
measure of expected structural response for a given earthquake or any kind vibrations and
also it ensures a simple and direct load path is provided for each frame. One of the aspects to
be considered while assessing the dynamic response of bridges subjected to live loads is the
problem of vibration. The passage of any load over a bridge causes the span to deflect from
the equilibrium position, causing a series of oscillations. This phenomenon continues till
either the structure comes back to its equilibrium position or is again activated by the passage
of another load. Therefore, “dynamic behaviour of bridge deck” needs to be studied. Using
IRC Class A loading bridge responses such as Bending Moment (BM) and deflection are
obtained to assess the serviceability. Further, with the help of SAP2000 software dynamic
analysis is done by Response Spectrum Method to obtain dynamic parameters such as natural
frequency and time period. This study aims at interpreting the output from the dynamic
analysis of the computer model of the bridge in order to check the resonance criteria.

1.1 Indian Road Congress

The Indian Road Congress (IRC) has formulated standard specifications and codes of practice
for road bridges with a view to establish a common procedure for the design and construction
of road bridges in India. The specifications are collectively known as the Bridge code. Prior

Received on January 2013 Published on March 2013 495

 Dynamic analysis of T-Beam bridge superstructure
Supriya Madda, Kalyanshetti M.G

to the formation of the IRC bridge code, there was no uniform code for the whole country.
Each state (or province) had its own rules about the standard loading and stresses.

The Indian Roads Congress (IRC) Bridge code as available now consists of eight sections as
below:

1. Section-I : General features of design

2. Section-II : Loads and stresses

3. Section-III : Cement concrete (Plain and reinforced)

4. Section-IV : Brick, stone and block masonry

5. Section-V : Steel road bridges

6. Section-VI : Composite construction

7. Section-VII : Foundations and Substructures

8. Section-VIII: Bearings

1.2 Dynamic behaviour of bridge deck

The dynamic characteristics of bridges are frequency, mode shapes and damping ratio of its
normal mode of vibration. These can be determined by the excitation of bridge, measure of
response, analysis of data. Determination of natural frequency is important since their
relation to frequency content of forcing function has major influence on the bridge response.
The natural period of vibration T (sec) of the structure is the time required for one cycle of
free vibration. It is related to the natural circular frequency of vibration ω (rad/sec) and the
natural cyclic frequency of vibration f (Hz) as follows:

T=

f= =

These frequencies are natural properties of the structure when it is allowed to vibrate freely
without any external excitation. In addition, the circular frequency ω is defined as:

Thus, the natural frequency of simply supported beam or bridge of uniform section depends
only on the mass (m) and stiffness of the structure (k). Vibration of bridges is a nuisance to
users because of associated physiological and psychological effects. The other reason to
control vibration is the structural one. The effect of vibration is to cause additional stresses in
the structure over and above the static effects. Certain thumb rule provisions incorporated in
the codes of practices such as limiting the ratio of deflection to span and restricting the span-
depth ratios, tend to make the structure more rigid and thus less prone to vibrations. But
these provisions are not based on evaluations of frequency and the amplitude of vibrations
likely to occur and hence cannot be taken as a guarantee against occurrence of undue
vibrations even under normal loads. Hence, dynamic analysis need to perform to obtain
dynamic parameters. Some of the methods are as follows

1. Time History Analysis

International Journal of Civil and Structural Engineering 496

Volume 3 Issue 3 2013
 Dynamic analysis of T-Beam bridge superstructure
Supriya Madda, Kalyanshetti M.G

2. Response Spectrum Analysis

3. Rayleigh Ritz Method

4. Finite Element Method

In this proposed study, bridge model is analyzed by Response Spectrum Analysis.

2. Response Spectrum Analysis

A plot of the peak value of a result of response quantity as a function of the natural vibration
period Tn of the system, or a related parameter such as circular frequency , or cyclic
frequency fn, is called the response spectrum for that quantity. Now, a central concept in
earthquake engg., the response spectrum provides a convinient means to summerize the peak
response of all possible linear Single Degree of Freedom (SDF) systems to perticular
component of ground motion. It has been adopted as a standard way of representation of
effect of ground acceleration on structures. It also provides a practical approach to apply the
knowledge of structural dynamics to the design of structures and development of lateral force
requirements in the building codes.

2.1 Parametric study

Dynamic analysis of T-beam bridge deck is done by Response Spectrum Analysis with the
help of SAP2000 software. A complete schedule of parametric study is given in table 1.

Table 1: List of studied parameters

Type of Bridge T-Beam Bridge

Span 15,20,25,30,35m

Lane of Bridge Two lane Four lane

Carriageway width 7.5 m 14 m

No. of longitudinal girders 3 3,4,5,6

Thickness of longitudinal
300mm 500mm
girders

No. of cross girders 5 5

Thickness of cross girders 250mm 250mm

Depth of deck slab 215mm 215mm

International Journal of Civil and Structural Engineering 497

Volume 3 Issue 3 2013
 Dynamic analysis of T-Beam bridge superstructure
Supriya Madda, Kalyanshetti M.G

Thickness of wearing coat 75mm 75mm

IRC standard live load Class A-2 trains Class A- 4 trains

Depth of longitudinal girder and cross girder is kept same for each bridge superstructure
model. For 15 m span, it is 1.575 m and for all the remaining spans it is 2 m. And this pattern
is same for all the considered cases in the present work. Parametric study is carried out as per
following cases

Table 2: list of cases of parametric study

Case No Lane Longitudinal Cross Span IRC

girders girders
Live load

Two Class A
Case-I 3 5 15,20,25,30,35
lane Loading

Four Class A
Case-II 3 5 15,20,25,30,35
lane Loading

Four Class A
Case-III 4 5 15,20,25,30,35
lane Loading

Four Class A
Case-IV 5 5 15,20,25,30,35
lane Loading

Four Class A
Case-V 6 5 15,20,25,30,35
lane Loading

All bridge models are prepared and analyzed using SAP2000. Bending moments, deflection
and deflection/span ratio of all the spans are determined. On the basis of which the
serviceability criteria is checked. This is followed by dynamic analysis of bridge to obtain
natural frequency and time period. With the help of these dynamic parameters, possibility of
resonance is checked. This is studied by parametric investigation and are presented in the
form of graph as follows

1. Variation of maximum total bending moment with respect to Span for 2 Lane bridge
superstructure with 3 longitudinal girders

2. Variation of maximum deflection with respect to with respect to Span for 2 Lane
bridge superstructure with 3 longitudinal girders

3. Variation of frequency with respect to Span for 2 Lane bridge superstructure with 3
longitudinal girders

International Journal of Civil and Structural Engineering 498

Volume 3 Issue 3 2013
 Dynamic analysis of T-Beam bridge superstructure
Supriya Madda, Kalyanshetti M.G

4. Variation of time period with respect to Span for 2 Lane bridge superstructure with 3
longitudinal girders

5. Variation of maximum total bending moment with respect to Span for 4 Lane bridge
superstructure

6. Variation of maximum deflection with respect to Span for 4 Lane bridge

superstructure

7. Variation of frequency with respect to Span for 4 Lane bridge superstructure

8. Variation of time period with respect to Span for 4 Lane bridge superstructure

Figure 1: Variation of Maximum total bending moment with respect to span for 2 lane bridge
superstructure

Figure 2: Variation of Maximum deflection with respect to span for 2 lane bridge
superstructure

International Journal of Civil and Structural Engineering 499

Volume 3 Issue 3 2013
 Dynamic analysis of T-Beam bridge superstructure
Supriya Madda, Kalyanshetti M.G

Figure 3: Variation of frequency with respect to span for 2 lane bridge superstructure

Figure 4: Variation of time period with respect to span for 2 lane bridge superstructure

International Journal of Civil and Structural Engineering 500

Volume 3 Issue 3 2013
 Dynamic analysis of T-Beam bridge superstructure
Supriya Madda, Kalyanshetti M.G

Figure 5: Variation of Maximum total bending moment with respect to span for 4 lane bridge
superstructure

Figure 6: Variation of Maximum deflection with respect to span for 4 lane bridge
superstructure

International Journal of Civil and Structural Engineering 501

Volume 3 Issue 3 2013
 Dynamic analysis of T-Beam bridge superstructure
Supriya Madda, Kalyanshetti M.G

Figure 7: Variation of frequency with respect to span for 4 lane bridge superstructure

Figure 8: Variation of time period with respect to span for 4 lane bridge superstructure

International Journal of Civil and Structural Engineering 502

Volume 3 Issue 3 2013
 Dynamic analysis of T-Beam bridge superstructure
Supriya Madda, Kalyanshetti M.G

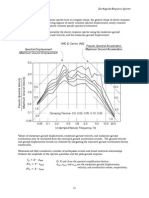
3. Observations

Following observations are obtained from detailed parametric study and above graphs:

1. Bending Moment in longitudinal girders: For two lane bridges, with the increase in
span, selfweight of bridge increases and hence maximum bending moment increases.
Rate of increase in BM is mild up to 25m, beyond that, rate increases. Thus for higher
span i.e. greater than 25m, BM in longitudinal girder increases with higher rate. This
trend is same for Four Lane Bridges also. But as the no. of longitudinal girders
increases, total BM decreases. 3 longitudinal girders case gives maximum total BM,
while 6 longitudinal girders case gives minimum value.

2. Deflection: Cross beams equalizes the deflections of the girders carrying heavy
loading with those of the girders with less loading. Hence in all girders deflection is
almost same. With the increase in span, deflection increases. In the case of Four Lane
Bridges, as the no. of longitudinal girder increases, deflection decreases. Deflection is
maximum for 3 longitudinal girders case and minimum for 6 longitudinal girders
case. For both the case, rate of increase in deflection is more up to 25 to 35m
comparing with span range 15 to 25.

3. Frequency and time period: For each span first mode shape gives least frequency and
max. time period. For shorter span frequency is on higher side which goes in reducing
with the increase in span and with the increase in span, time period goes on
increasing. For four lane case, as the no. of longitudinal girders increases, frequency
increases and time period decreases.

Limiting Value for deflection/span ratio is = 2.66x10-3 as specified by IRC. From this
value, serviceability criteria can be checked. Frequency of vehicle (passing over bridge) is
considered between 3 – 5 Hz. This frequency need to be avoided to prevent resonance.

4. Conclusions

This proposed study is carried out for two lane and four lane bridges of spans 15m, 20m,
35m, 30m and 35m using IRC class A loading by varying a number of longitudinal girders.
SAP2000 software is used for this work.

Following conclusions may be drawn from the graphs (figure 1 to figure 8 ) and observations

1. For two lane bridges, all the bridge spans except 35 m, give reasonable results of
deflection/span ratio, which are acceptable. But for span 35m (2.51x10-3), it is very
close to permissible limit (2.66x10-3) which may lead to serviceability problems in
future. Same will be situation for similar kind of bridge beyond a span of 35 m.

2. For four lane bridges, Deflection/span ratio values for shorter spans i.e. up to 30 m
are within permissible limit for all the combinations of longitudinal girders. But for 35
m span, of 3 LG (2.665x10-3) and 5 LG (2.19x10-3) systems, there is no marginal
difference between actual and permissible value (2.66x10-3). Hence, it is quite
possible that, they may lead to serviceability problems.

3. Vehicle frequency is considered between 3 – 5 Hz. Hence, frequency of bridge

superstructure should not fall in the vehicle frequency band to avoid resonance.
However, the frequency for span 25m and 30m of two lane bridges fall in the vehicle
frequency band of 3 – 5 Hz. Hence, there may arise issues related with vibration. It
may be safe to state that, all other spans will not pose any vibration related problems.

International Journal of Civil and Structural Engineering 503

Volume 3 Issue 3 2013
 Dynamic analysis of T-Beam bridge superstructure
Supriya Madda, Kalyanshetti M.G

4. For Four lane bridges, similar to Two Lane Bridge case, the frequency of bridge
superstructure for span 25m and 30m fall in the vehicle frequency band of 3 – 5 Hz.
Hence, there may arise issues related with vibration.

5. It may be safe to state that, all other spans will not pose any vibration related
problems as they do not fall in the vehicle frequency band. It may be said that,
medium range span bridge i.e. 25 to 30 m will be subject to vibration problems.
However, too short or long span bridges may not create vibration related problems.

5. References

1. Azad A.K and El-Boghdadi M.H, Static Analysis of Multibeam Bridge deck, 4th
Saudi Engg. Conference, Nov. 1995. Ayman M. Elmahdy, Hisham A. Elarobaty, El
Mostafa M. Higazy & Mohammad N. Fayed, “Dynamic Behaviour of Bridge/Vehicle
Interactive Systems”, 12th International Colloquium on Structural & Geotech Engg. at
Cairo-Egypt, Dec. 2007

2. Melcer., (2006), Vehicle - Road interaction, Analysis in a frequency domain, Slovak

Journal of Civil Engineering, 3(4), pp 48-52.

3. Munirudrappa and Dhruvaraja Iyengar, Dynamic Analysis of Continuous Span

Highway Bridge, ISET Journal of Earthquake Technology, Paper No. 392, Vol. 392,
March 1999.

4. Mohamad Najim Mahmood and Ayad Thabit Saeed Al-Ghabsha., (2006), Dynamic
analysis of bridges subjected to moving vehicles, Al-Rafidain Engineering, 14(4).

5. IRC: 1984, Special report: State of the Art Dynamic Behaviour of Highway Bridges.

6. Johnson Victor, Essentials of Bridge Engineering, Oxford & IBH Publishing

Company Pvt, Ltd. New Delhi.

7. IRC: 1984, Special report : State of the Art Dynamic Behaviour of Highway Bridges.

8. IRC:5-1998- Standard Specifications and Code of Practice for Road Bridges,

Section I – General Features of Design (Seventh Revision)

9. Pankaj Agarwal & Manish Shrikhande, Earthquake Resistant Design of Structures,

Pentice hall of India private Limited, New Delhi.

International Journal of Civil and Structural Engineering 504

Volume 3 Issue 3 2013