ECON 302: Intermediate Macroeconomic Theory (Spring 2012-13)

Discussion Section Week 3 – February 8, 2013

SOME KEY CONCEPTS

- Total factor productivity across countries
- The Solow growth model (Capital accumulation equation, steady state)

EXERCISE
Question 1 (Backing out the total factor productivity)
Suppose we observe in the data that output per capita in Country A and B are $10,000 and $500, respectively.
The capital stock per person of Country A and B are $20,000 and $2,500, respectively. Assume that capital
income share is 1/3. What can be said about the productivity of both countries?

Question 2 (The preliminary of Solow growth model)

a) Capital accumulation equation
Write down the capital accumulation equation from the following information, write down step-by-step:
“Capital stock next year, Kt+1 , comes from capital stock this year, Kt , depreciated by d and investment this
1/3 2/3
year, It . Investment is a fixed proportion of s of output, Yt . The output is given by Yt = AKt L . Labor
supply, L, and productivity, A, are exogenously constant.”
Express the capital accumulation equation in terms of capital stock, Kt , and per capita capital stock, Kt /L.

b) Numerical example
Now suppose that d = 10%, s = 25%, A = 10 and L = 8, what is the capital accumulation equation expressed
in both Kt and kt ?

c) Steady-state level of capital and output (Please excuse the number, it’s ugly! So don’t worry
about it.)
Solve for the steady-state level of capital, K ⇤ , in terms of parameters outlined in a), then apply the numbers
from part b). Solve for the steady-state level of output, Y ⇤ , in terms of parameters.

d) Consumption
In light of what we have established in part a), write out the equation for consumption Ct .

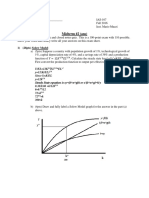
e) Drawing the Solow diagram (See Figure 5.1-5.2, p.p. 105-107)

From the capital accumulation equation written in part a), draw the Solow diagram, i.e. in the same graph
with Kt on horizontal axis and investment and depreciation on vertical axis, draw sYt and dKt separately.

Question 3 (Comparative analysis under Solow growth model)

Taking the answers from Question 2, we wish to explain cross-country income variation. What is the long-
run effect towards steady-state level of capital stock, K ⇤ , and output, Y ⇤ , when there is a change to each of
the following parameters: s, d, A, L and a (the capital share)? Repeat the analysis for per capita variables.
In some cases, draw the Solow diagram with two cases of each parameter. Summarize in the following table:

Country with Effect towards K ⇤ Effect towards Y ⇤ Effect towards k ⇤ Effect towards y ⇤
Higher s
Higher d
Higher A
Higher L
Higher a