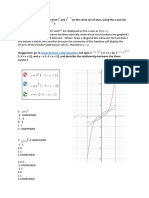
"if we graph both f and f −1 on the same set of axes, using the x-axis for the input to both f

and f −1, We notice a distinct relationship: The graph of f −1 ( x) is the graph of f ( x )reflected
about the diagonal line y = x, which we call the identity line."( Abramson, 2017, p.262)

I will make my own example:

1 −1 1
f ( x )= f (x)= −1
1+ x x

actually, I did not find any difficulty, but on the contrary, I see that determining the functions
in this way and graphing them on the same axes, clarifies the nature of the relationship
between the inverted functions and confirms the validity of our calculations.

f ( x )=x +1 f 2=f ° f =( x+ 1 )+1=x+ 3f 2 ° f =( x+1 )+3=x +4 f ° f 2=( x+ 3 )+ 1=x +4

So, the relation f ° f 2=f 2 ° f is true, because f 2 is a composition of the same function ( f ° f )

If we suppose g ( x )=x 2+3

f ° g=¿ ( x 2+ 3 ¿+1=x 2+ 4 g ° f =( x+ 1)2 +3=x2 +2 x+ 4

We have a different result, so we couldn't say the set is infinite

Reference
Abramson, J. (2017). Algebra and trigonometry. OpenStax, TX: Rice University.
Retrieved from https://openstax.org/details/books/algebra-and-trigonometry