Brac University

Department of Mathematics and Natural Sciences

Midterm examination (Set A) Fall 2020

Course: Differential Geometry Code: MAT313

Full Marks: 25 Time: 3hr

Carefully read all the questions before answering them appropriately

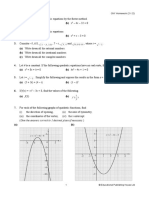
1. (a) Let a bijective map F : R2 → R2 be given by

F (x, y) = (x2 + y 2 , 2x + y 2 ).

Find the differential DF of the map F given above and locate the points of R2 by sketching a graph
in the x-y plane where F fails to be invertible. Now given the fact that F is invertible at (0, 0), find
−1
differential DF −1 of the inverse map F −1 at (0, 0), i.e., find DF(0,0) .

(b) Given the equation (x2 + y 2 + 2z 2 )1/2 − cos z = 0, is it possible for one to solve y uniquely in
terms of x and z in a neighbourhood of (0, 1, 0)? For the same equation, is it possible to write z in
terms of x and y uniquely near the same point (0, 1, 0)?
((2+2+2)+(2+2))

2. (a) Prove that open subset of a smooth manifold is also a smooth manifold.

(b) Let M (n, C) be the set of all (n×n) matrices with entries belonging to the set of complex numbers
C. Consider the following subset of M (n, C):

GL(n, C) = {A ∈ M (n, C) | det A �= 0}.

Prove that GL(n, C) is a smooth manifold.

(c) Given two subsets V1 and V2 of the Euclidean plane R2 , with V1 = R2 \ V1 and V2 = R2 \ V2
where V1 = {(x, y) | y = 0, x ≤ 0} and V2 = {(x, y) | y = 0, x ≥ 0}. Define charts (V1 , ψ1 ) and
(V2 , ψ2 ) on R2 using polar coordinates. First, show that these 2 charts do not form an atlas for R2 .
Now consider the chart (V3 , ψ3 ) with V3 = R2 and φ3 = id, the identity map on R2 . Now, show that
{(V3 , ψ3 ), (V1 , ψ1 )} forms a smooth atlas on R2 .
(5+2+3)

3. (a) Argue why C ∞ compatibility of charts is not an equivalence relation.

(b) Consider Z as a subset of R equipped with the usual topology. If n ∈ Z, then prove that {n} is
open in the subspace topology on Z induced by the usual topology on R. (3+2)