UCSI International School

Inequality Graphs and Similarity

IGCSE Extended Revision

20.3.17

1. Answer the whole of this question on a sheet of graph paper.

A taxi company has “SUPER” taxis and “MINI” taxis.
One morning a group of 45 people needs taxis.

For this group the taxi company uses x “SUPER” taxis and y “MINI” taxis.
A “SUPER” taxi can carry 5 passengers and a “MINI” taxi can carry 3 passengers.
So 5x + 3y ≥ 45.

(a) The taxi company has 12 taxis.

Write down another inequality in x and y to show this information.
[1]

(b) The taxi company always uses at least 4 “MINI” taxis.

Write down an inequality in y to show this information.
[1]

(c) Draw x and y axes from 0 to 15 using 1 cm to represent 1 unit on each axis.
[1]

(d) Draw three lines on your graph to show the inequality 5x + 3y ≥ 45 and the inequalities
from parts (a) and (b).
Shade the unwanted regions.
[6]

(e) The cost to the taxi company of using a “SUPER” taxi is $20 and the cost of using a
“MINI” taxi is $10.
The taxi company wants to find the cheapest way of providing “SUPER” and “MINI”
taxis for this group of people.
Find the two ways in which this can be done.
[3]

(f) The taxi company decides to use 11 taxis for this group.
(i) The taxi company charges $30 for the use of each “SUPER” taxi and $16 for the

© Doublestruck & CIE - Licensed to UCSI International School 1

 use of each “MINI” taxi.
Find the two possible total charges.
[3]

(ii) Find the largest possible profit the company can make, using 11 taxis.
[1]

2. Answer the whole of this question on a sheet of graph paper.

Tiago does some work during the school holidays.

In one week he spends x hours cleaning cars and y hours repairing cycles.
The time he spends repairing cycles is at least equal to the time he spends cleaning cars.
This can be written as y ≥ x.

He spends no more than 12 hours working.

He spends at least 4 hours cleaning cars.

(a) Write down two more inequalities in x and/or y to show this information.
[3]

(b) Draw x and y axes from 0 to 12, using a scale of 1 cm to represent 1 unit on each axis.
[1]

(c) Draw three lines to show the three inequalities. Shade the unwanted regions.
[5]

(d) Tiago receives $3 each hour for cleaning cars and $1.50 each hour for repairing cycles.

(i) What is the least amount he could receive?

[2]

(ii) What is the largest amount he could receive?

[2]

© Doublestruck & CIE - Licensed to UCSI International School 2

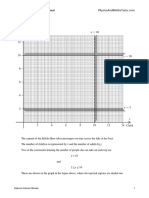
3.
y
6

0 x
1 2 3 4 5 6

–1

–2

–3

–4

–5

(a) Draw the three lines y = 4, 2x – y = 4 and x + y = 6 on the grid above.

[4]

(b) Write the letter R in the region defined by the three inequalities below.

y≤4 2x – y ≥ 4 x+y≥6
[1]

© Doublestruck & CIE - Licensed to UCSI International School 3

4. A new school has x day students and y boarding students.

The fees for a day student are $600 a term.

The fees for a boarding student are $1200 a term.
The school needs at least $720 000 a term.

(a) Show that this information can be written as x + 2y ≥ 1200.

Answer (a) ……….….…………

[1]

(b) The school has a maximum of 900 students.

Write down an inequality in x and y to show this information.

Answer (b) ……….….…………

[1]

(c) Draw two lines on the grid below and write the letter R in the region which represents
these two inequalities
y
900

N um ber of
b o a rd in g
s tu d e n ts

x
0
N u m b e r o f d a y s tu d e n ts 1200
[4]

(d) What is the least number of boarding students at the school?

© Doublestruck & CIE - Licensed to UCSI International School 4

 Answer (d) ……….….…………
[1]

5. Two similar vases have heights which are in the ratio 3 : 2.

3
(a) The volume of the larger vase is 1080 cm .
Calculate the volume of the smaller vase.

3
Answer (a) ……………………… cm
[2]

2
(b) The surface area of the smaller vase is 252 cm .
Calculate the surface area of the larger vase.

2
Answer (b) ……………………… cm
[2]

6. A spherical balloon of radius 3 metres has a volume of 36π cubic metres.

It is further inflated until its radius is 12 m.
Calculate its new volume, leaving your answer in terms of π.

3
Answer …………………………… m
[2]

7. A cylindrical glass has a radius of 4 centimetres and a height of 6 centimetres.

A large cylindrical jar full of water is a similar shape to the glass.
The glass can be filled with water from the jar exactly 216 times.

© Doublestruck & CIE - Licensed to UCSI International School 5

 Work out the radius and height of the jar.

Answer radius ……………… cm

height ……………… cm
[3]

© Doublestruck & CIE - Licensed to UCSI International School 6

8. A statue two metres high has a volume of five cubic metres.
A similar model of the statue has a height of four centimetres.

(a) Calculate the volume of the model statue in cubic centimetres.

3
Answer (a) …….……………………. cm
[2]

(b) Write your answer to part (a) in cubic metres.

Answer 3
(b) …….……..………………. m
[1]

9. A company makes two models of television.

Model A has a rectangular screen that measures 44 cm by 32 cm.
Model B has a larger screen with these measurements increased in the ratio 5 : 4.

(a) Work out the measurements of the larger screen.

Answer (a) ………… cm by ………… cm

[2]

model A screen area

(b) Find the fraction model B screen area in its simplest form.

Answer (b) ………………………………

[1]

© Doublestruck & CIE - Licensed to UCSI International School 7

10.

A
B
55

4 0 .3 c m
2 6 .8 c m
92

X 2 0 . 1 cc mm

D NOT TO SCALE

A, B, C and D lie on a circle. AC and BD intersect at X. Angle ABX = 55° and angle AXB = 92°.
BX = 26.8 cm, AX = 40.3 cm and XC = 20.1 cm.

(i) Calculate the area of triangle AXB

You must show your working.

[2]

(ii) Calculate the length of AB.

You must show your working.

[3]

(iii) Write down the size of angle ACD. Give a reason for your answer.

[2]

(iv) Find the size of angle BDC.

[1]

(v) Write down the geometrical word which completes the statement

© Doublestruck & CIE - Licensed to UCSI International School 8

 “Triangle AXB is to triangle DXC.”
[1]

(vi) Calculate the length of XD.

You must show your working.

[2]

© Doublestruck & CIE - Licensed to UCSI International School 9