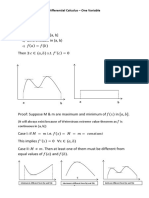
Rolle’s theorem

Statement: If a function 𝑓(𝑥) is

1. Continuous in the closed interval [𝑎, 𝑏]
2. Differentiable in the open interval (𝑎, 𝑏)
3. 𝑓(𝑎) = 𝑓(𝑏)
Then there exists at least one value of 𝑥 (say c) between a and b such that
𝑓 ′ (𝑐) = 0

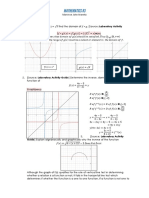
Example 1: Verify Rolle’s theorem for the function 𝑓(𝑥) = (𝑥 − 2)(𝑥 − 3)(𝑥 − 4) in the
interval (2, 3).
Solution: Given that 𝑓(𝑥) = (𝑥 − 2)(𝑥 − 3)(𝑥 − 4)
∴ 𝑓(𝑥) = (𝑥 2 − 5𝑥 + 6)(𝑥 − 4)
∴ 𝑓(𝑥) = 𝑥 3 − 9𝑥 2 + 26𝑥 − 24
∴ 𝑓 ′ (𝑥) = 3𝑥 2 − 18𝑥 + 26
∴ 𝑓 ′ (𝑐) = 3𝑐 2 − 18𝑐 + 26

Let 𝑎 = 2 and 𝑏 = 3
∴ 𝑓(𝑎) = 𝑓(2) = (2 − 2)(2 − 3)(2 − 4) = 0
∴ 𝑓(𝑏) = 𝑓(3) = (3 − 2)(3 − 3)(3 − 4) = 0
∴ 𝑓(𝑎) = 𝑓(𝑏)
Since 𝑓(𝑥) is a algebraic polynomial function in x, so the function is continuous and differentiable
of the given interval.
Therefore, all the three conditions of Rolle’s theorem are satisfied.
𝑓 ′ (𝑐) = 0
⟹ 3𝑐 2 − 18𝑐 + 26 = 0

−(−18) ± √(−18)2 − 4.3.26

∴𝑐=
2.3
∴ 𝑐 = 3.57; 2.43
Since 𝑐 = 2.43 lies in the interval (2, 3).
Hence, Rolle’s theorem is verified.
H.W.
2⁄
1. Verify mean-value theorem for the function 𝑓(𝑥) = 𝑥 3 in the interval (−2,1).
2. Verify mean-value theorem for the function 𝑓(𝑥) = 𝑥 2 + 5𝑥 − 6, in the interval [−6, 1]
3. Verify mean-value theorem for the function 𝑓(𝑥) = 10 − 𝑥2 , in the interval [0, 10]