Professional Documents
Culture Documents
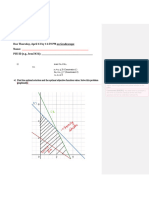
3.2 Unconstrained Optimization Multiple Variables
Uploaded by
SHYAM SUNDAR0 ratings0% found this document useful (0 votes)
9 views11 pagesOriginal Title
3.2-Unconstrained-Optimization-Multiple-Variables
Copyright
© © All Rights Reserved
Available Formats
PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
0 ratings0% found this document useful (0 votes)
9 views11 pages3.2 Unconstrained Optimization Multiple Variables
Uploaded by
SHYAM SUNDARCopyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
You are on page 1of 11
Unconstrained Optimization:
Multiple Variables
Basic Math for Economics – Refresher
Eric Dunaway epdunaway@gmail.com 1
Introduction
While working with just one variable is simple, it’s rare in
economics.
Often, we must work with many variables all at the same
time.
This complicates our optimization slightly, but the same rules
still apply.
Let’s take a look at another unconstrained optimization
problem, but this time through the lens of a Cournot duopoly.
Recallthat in a Cournot duopoly, two firms simultaneously
choose their quantities, but face the same market price.
Eric Dunaway epdunaway@gmail.com 2
Unconstrained Optimization
Let’s use the same market as last time, but rather than there
being a monopolist, now there are two firms and they
compete in quantities.
Both firms face the inverse demand function
𝑝 = 250 − 2𝑞1 − 2𝑞2
and face constant marginal costs of production of 𝑐 = 50.
As before, we will set up our problem and then optimize.
Note that we actually have two optimization problems here.
Each firm is maximizing their profits separately, so we
need to treat them as separate optimization decisions.
Eric Dunaway epdunaway@gmail.com 3
Unconstrained Optimization
Let’s start with firm 1.
They want to maximize their profits, and the only thing
they can choose is their own quantity, 𝑞1 . Thus, we
have,
max
𝑞1
Next, they want to maximize their own profits (they
don’t care about firm 2’s profits at all), but their inverse
demand function is also a function of firm 2’s quantity,
so we must include it.
max 250 − 2𝑞1 − 2𝑞2 𝑞1 − 50𝑞1
𝑞1
Eric Dunaway epdunaway@gmail.com 4
Unconstrained Optimization
max 250 − 2𝑞1 − 2𝑞2 𝑞1 − 50𝑞1
𝑞1
From here, we can calculate a first-order condition as before
(remember to treat 𝑞2 as a constant),
𝜕𝜋1
= 250 − 4𝑞1 − 2𝑞2 − 50 = 0
𝜕𝑞1
We can perform the same analysis for firm 2, obtaining the following
optimization problem,
max 250 − 2𝑞1 − 2𝑞2 𝑞2 − 50𝑞2
𝑞2
and first-order condition,
𝜕𝜋2
= 250 − 2𝑞1 − 4𝑞2 − 50 = 0
𝜕𝑞2
Eric Dunaway epdunaway@gmail.com 5
Unconstrained Optimization
𝜕𝜋1
= 250 − 4𝑞1 − 2𝑞2 − 50 = 0
𝜕𝑞1
𝜕𝜋2
= 250 − 2𝑞1 − 4𝑞2 − 50 = 0
𝜕𝑞2
This is just a system of two equations and two unknowns
and fairly easy to solve.
Doing so yields 𝑞1∗ = 𝑞2∗ = 33.3, which is notable smaller
than what a monopolist produces (which is expected).
Westill need to check whether this is a maximum,
however.
Eric Dunaway epdunaway@gmail.com 6
Unconstrained Optimization
𝜕𝜋1
= 250 − 4𝑞1 − 2𝑞2 − 50 = 0
𝜕𝑞1
𝜕𝜋2
= 250 − 2𝑞1 − 4𝑞2 − 50 = 0
𝜕𝑞2
This is a bit harder, and requires the use of a matrix called the Hessian.
To calculate the Hessian, we need to take a derivative of each of our
first-order conditions for each of our choice variables (4 derivatives
total in this case).
The first row and first column of our Hessian is the derivative of our
first first-order condition for our first variable.
Thefirst row and second column of our Hessian is the derivative of
our first first-order condition for our second variable.
Eric Dunaway epdunaway@gmail.com 7
Unconstrained Optimization
Calculating these derivatives,
𝜕 2 𝜋1 𝜕 2 𝜋1
2 = −4 𝜕𝑞1 𝜕𝑞2
= −2
𝜕𝑞1
𝐻=
𝜕 2 𝜋2 𝜕 2 𝜋2
= −2 2 = −4
𝜕𝑞2 𝜕𝑞1 𝜕𝑞2
Or, reducing this matrix a little bit, we have
−4 −2
𝐻=
−2 −4
Our problem is maximized if this matrix is negative
semidefinite.
Eric Dunaway epdunaway@gmail.com 8
Unconstrained Optimization
−4 −2
𝐻=
−2 −4
Negative semidefinite?
Leaving out most of the math, it means that certain
elements of the Hessian must take certain values.
For a 2x2 matrix, if all the elements along the trace are
less than or equal to zero and the determinant is positive,
then the matrix is negative semidefinite.
First,
let’s check the trace. Both elements along the
trace are equal to −4, so they satisfy the requirement
that they are less than or equal to zero.
Eric Dunaway epdunaway@gmail.com 9
Unconstrained Optimization
−4 −2
𝐻=
−2 −4
Now, let’s calculate the determinant.
𝐻 = −4 −4 − −2 −2 = 16 − 4 = 12
Since the determinant of the Hessian is positive, that
along with all the elements of our trace being negative
means that our matrix is negative semidefinite and we
have a maximum rather than a minimum.
It’s
useful to check this when dealing with less
behaved functional forms.
Eric Dunaway epdunaway@gmail.com 10
Unconstrained Optimization
If you are looking for a minimum, rather than a maximum,
the Hessian needs to be positive semidefinite.
For a 2x2 Hessian, all the elements along the trace must
be greater than or equal to zero while the determinant
is still positive.
If we move beyond a 2x2 Hessian (i.e., we have more
than two choice variables), this becomes more
complicated.
Our principal minors must have alternating signs based
upon which minor they are.
A linear algebra course would be helpful for this.
Eric Dunaway epdunaway@gmail.com 11
You might also like
- Introduction To The Simplex AlgorithmDocument62 pagesIntroduction To The Simplex AlgorithmKarim CHERIFINo ratings yet
- 18 Dual Simplex & SensitivityDocument17 pages18 Dual Simplex & SensitivitySiddhanth SharmaNo ratings yet
- Unit 1 Linear Programming For CanvasDocument11 pagesUnit 1 Linear Programming For CanvasSayaNo ratings yet
- Problem Set 2Document12 pagesProblem Set 2udNo ratings yet
- 1L LP Transformation TricksDocument12 pages1L LP Transformation TrickscaspersoongNo ratings yet
- 15.053 February 22, 2007: Introduction To The Simplex AlgorithmDocument62 pages15.053 February 22, 2007: Introduction To The Simplex AlgorithmEhsan SpencerNo ratings yet
- Equations, Inequalities, and VICs PDFDocument7 pagesEquations, Inequalities, and VICs PDFsahil jainNo ratings yet
- Numerical MethodDocument31 pagesNumerical MethodAhmed AbdullaNo ratings yet
- PERTDocument75 pagesPERTJISHA PDNo ratings yet
- Quantitative Techniques in Project Management: Unit I March 31, 2022Document20 pagesQuantitative Techniques in Project Management: Unit I March 31, 2022Mandar GupteNo ratings yet
- Dr. Joon-Yeoul Oh: IEEN 5335 Principles of OptimizationDocument33 pagesDr. Joon-Yeoul Oh: IEEN 5335 Principles of OptimizationSoumojit KumarNo ratings yet
- A. Exponential Equation, Inequalities and FunctionDocument8 pagesA. Exponential Equation, Inequalities and FunctionGELYNNE LOPEZNo ratings yet
- Graphing and Solving InequalitiesDocument9 pagesGraphing and Solving InequalitiesMr. PetersonNo ratings yet
- Unit 2 - Divide and Conquer & Greedy StrategyDocument45 pagesUnit 2 - Divide and Conquer & Greedy StrategyDj adityaNo ratings yet
- UCK 337 Introduction To Optimization Spring 2019-2020 Problem Set IDocument3 pagesUCK 337 Introduction To Optimization Spring 2019-2020 Problem Set IMim Alperen YarenNo ratings yet
- Constrained Limitations Performance Limitation: OptimizationDocument5 pagesConstrained Limitations Performance Limitation: OptimizationjohnNo ratings yet
- 4 Rational Equations and InequalitiesDocument23 pages4 Rational Equations and InequalitiesKelvin Mark KaabayNo ratings yet
- ISE 303 - Chapter 3Document58 pagesISE 303 - Chapter 3mohammed aliNo ratings yet
- Manonmaniam Sundaranar University: B.Sc. Mathematics - Iii YearDocument76 pagesManonmaniam Sundaranar University: B.Sc. Mathematics - Iii YearNikk TirthNo ratings yet
- Duality in Linear ProgrammingDocument17 pagesDuality in Linear ProgrammingArjun SubediNo ratings yet
- Class 1 BookDocument50 pagesClass 1 BookMohammed YasserNo ratings yet
- Solving One-Variable Inequalities 9.1.1 and 9.1.2: Example 1Document53 pagesSolving One-Variable Inequalities 9.1.1 and 9.1.2: Example 1Letsirk ScarletNo ratings yet
- HW 13Document6 pagesHW 13HarshitaNo ratings yet
- Simplex Method - 4th Semester - Numerical ProgrammingDocument37 pagesSimplex Method - 4th Semester - Numerical ProgrammingMyWBUT - Home for Engineers100% (1)
- CQV Perspectives 1Document13 pagesCQV Perspectives 1GregoriusNo ratings yet
- Lesson 2: Linear Programming: ObjectivesDocument11 pagesLesson 2: Linear Programming: ObjectivesHarvey AguilarNo ratings yet
- Unit 6 PDFDocument28 pagesUnit 6 PDFsaksham sharmaNo ratings yet
- Rules of ExponentsDocument4 pagesRules of ExponentsB01 BASILIO, MICHAEL ANGELO L.No ratings yet
- v2 - Algebra II (Common Core) Regents Review Sheet - Facts You Must Know ColdDocument19 pagesv2 - Algebra II (Common Core) Regents Review Sheet - Facts You Must Know ColdIkhri574No ratings yet
- Linear Programming (Chapter 11) : No Problem Can Stand The Assault of Sustained ThinkingDocument14 pagesLinear Programming (Chapter 11) : No Problem Can Stand The Assault of Sustained ThinkingEl MayimbeNo ratings yet
- Solving Linear Equations - Absolute ValueDocument6 pagesSolving Linear Equations - Absolute ValueMalhea VegeniaNo ratings yet
- Week 4 Quadratic InequaltiiesDocument31 pagesWeek 4 Quadratic InequaltiiesArriane VillaflorNo ratings yet
- Slides 3 - Simplex MethodDocument30 pagesSlides 3 - Simplex MethodINU-51-Nihar NimsarkarNo ratings yet
- Chapter 5 Linear ProgrammingDocument8 pagesChapter 5 Linear ProgrammingJhan Ray Gomez Barril100% (1)
- Chapter 1-Algebra dbm10133Document54 pagesChapter 1-Algebra dbm10133Nisa ArNo ratings yet
- IE380 Unit 9Document50 pagesIE380 Unit 9ayçaNo ratings yet
- Lesson 1: UNIT 1: Quadratic EquationsDocument31 pagesLesson 1: UNIT 1: Quadratic EquationsJaylaica EstrechoNo ratings yet
- Math 9 Q2 Module 5Document12 pagesMath 9 Q2 Module 5Hannah Lunas100% (1)
- Answer Key: Laws of ExponentsDocument3 pagesAnswer Key: Laws of Exponentsdiarrhea queenNo ratings yet
- Chapter 4 Duality and Post Optimal AnalysisDocument37 pagesChapter 4 Duality and Post Optimal AnalysisMir Md Mofachel HossainNo ratings yet
- Optimization L13 14Document55 pagesOptimization L13 14Sahil chowdhryNo ratings yet
- Operations Research: Integer ProgrammingDocument42 pagesOperations Research: Integer ProgrammingAndri IndriawanNo ratings yet
- CHAPTER 7 EquationsDocument11 pagesCHAPTER 7 EquationsSathish Sarma SathianarayananNo ratings yet
- 14 Dual Simplex 2023 NDocument37 pages14 Dual Simplex 2023 NMohammad Ishraq HossainNo ratings yet
- The Simplex Algorithm: Putting Linear Programs Into Standard Form Introduction To Simplex AlgorithmDocument25 pagesThe Simplex Algorithm: Putting Linear Programs Into Standard Form Introduction To Simplex AlgorithmmritroyNo ratings yet
- Mathematics in The Modern World ReviewerDocument4 pagesMathematics in The Modern World ReviewerCha Pitacio100% (12)
- Linear Inequalities: 6.1 OverviewDocument16 pagesLinear Inequalities: 6.1 OverviewAli Asgar BeguwalaNo ratings yet
- Solving Optimization Problems: Lesson 6.2Document42 pagesSolving Optimization Problems: Lesson 6.2Hannah Gliz PantoNo ratings yet
- The Simplex Algorithm: Prof. Dr. M. Arslan ÖRNEKDocument59 pagesThe Simplex Algorithm: Prof. Dr. M. Arslan ÖRNEKMerlin KNo ratings yet
- Linear Programming - Brilliant Math & Science WikiDocument19 pagesLinear Programming - Brilliant Math & Science WikiILLA PAVAN KUMAR (PA2013003013042)No ratings yet
- Equation and Inequalities 1Document5 pagesEquation and Inequalities 1avik palNo ratings yet
- 1.1 Solving Linear EquationsDocument4 pages1.1 Solving Linear EquationsAna RamirezNo ratings yet
- 5-2 Study Guide and Intervention: Solving Inequalities by Multiplication and DivisionDocument2 pages5-2 Study Guide and Intervention: Solving Inequalities by Multiplication and DivisionReham Mohamed Ahmed NoufalNo ratings yet
- How To Solve Absolute Value EquationsDocument5 pagesHow To Solve Absolute Value Equationsapi-126876773No ratings yet
- PowerpointDocument10 pagesPowerpointapi-467445171No ratings yet
- Beginning at The Very Beginning: Pre-Pre-Calculus: Reviewing Order of Operations: The Fun in FundamentalsDocument13 pagesBeginning at The Very Beginning: Pre-Pre-Calculus: Reviewing Order of Operations: The Fun in FundamentalsLiandysan23No ratings yet
- Tutorial 7 Matrix Algebra For Homogeneous Linear Algebraic SystemDocument3 pagesTutorial 7 Matrix Algebra For Homogeneous Linear Algebraic System徐子裕No ratings yet
- Attacking Problems in Logarithms and Exponential FunctionsFrom EverandAttacking Problems in Logarithms and Exponential FunctionsRating: 5 out of 5 stars5/5 (1)
- L UsDocument2 pagesL UsSHYAM SUNDARNo ratings yet
- Ugc RK Vikas - JRDocument20 pagesUgc RK Vikas - JRSHYAM SUNDARNo ratings yet
- Notice Payment of Fees-16092022Document1 pageNotice Payment of Fees-16092022SHYAM SUNDARNo ratings yet
- Calculate The Shear Force and Bending Moment For The Beam Subjected To A Concentrated Load As Shown in The FigureDocument1 pageCalculate The Shear Force and Bending Moment For The Beam Subjected To A Concentrated Load As Shown in The FigureSHYAM SUNDARNo ratings yet
- ScoeDocument25 pagesScoeSHYAM SUNDARNo ratings yet
- NSP Circular 2022Document2 pagesNSP Circular 2022SHYAM SUNDARNo ratings yet
- Circular Zeroth Project ReviewDocument1 pageCircular Zeroth Project ReviewSHYAM SUNDARNo ratings yet
- Essai NT PPT FinalDocument20 pagesEssai NT PPT FinalSHYAM SUNDARNo ratings yet
- FFF 3D Printing Technique Investigation On Mechanical and Thermal Properties of Polycarbonate Polymer Reinforced Glass and Carbon Fiber CompositesDocument1 pageFFF 3D Printing Technique Investigation On Mechanical and Thermal Properties of Polycarbonate Polymer Reinforced Glass and Carbon Fiber CompositesSHYAM SUNDARNo ratings yet
- Maeol Test CentreDocument5 pagesMaeol Test CentreSHYAM SUNDARNo ratings yet
- Rubn NT PPT FinalDocument11 pagesRubn NT PPT FinalSHYAM SUNDARNo ratings yet
- What Is Wear? 1.1 DefinitionDocument18 pagesWhat Is Wear? 1.1 DefinitionSHYAM SUNDARNo ratings yet
- Puducherry Technological University: Nanotechnology NanosensorsDocument17 pagesPuducherry Technological University: Nanotechnology NanosensorsSHYAM SUNDARNo ratings yet
- Safety Data Sheet: 1. Identification of The Substance/Preparation and of The Company/UndertakingDocument7 pagesSafety Data Sheet: 1. Identification of The Substance/Preparation and of The Company/UndertakingSHYAM SUNDARNo ratings yet
- Final Recruitment Notificaiton Dated 25.5.22Document6 pagesFinal Recruitment Notificaiton Dated 25.5.22SHYAM SUNDARNo ratings yet
- Preyesh - Design For Environmental and Substainable DesignDocument18 pagesPreyesh - Design For Environmental and Substainable DesignSHYAM SUNDARNo ratings yet
- Polymercomposites-ExperimentalAnalysisandTheoreticalModelingofthe TTLawDocument12 pagesPolymercomposites-ExperimentalAnalysisandTheoreticalModelingofthe TTLawSHYAM SUNDARNo ratings yet
- Mini Project - Zeroth Review Presented by T.Praveen Kumar (21me324) K.Vamanan (21me331)Document8 pagesMini Project - Zeroth Review Presented by T.Praveen Kumar (21me324) K.Vamanan (21me331)SHYAM SUNDARNo ratings yet
- Puducherry Technological University: (An Autonomous Institution of Govt. of Puducherry)Document19 pagesPuducherry Technological University: (An Autonomous Institution of Govt. of Puducherry)SHYAM SUNDARNo ratings yet
- Completely Randomized Design : Unit - II (Design of Experiments)Document6 pagesCompletely Randomized Design : Unit - II (Design of Experiments)SHYAM SUNDARNo ratings yet
- JRPC-InjectionmoldedshortglassandcarbonfibersDocument13 pagesJRPC-InjectionmoldedshortglassandcarbonfibersSHYAM SUNDARNo ratings yet
- Sona Namitha - Cost EvauationDocument31 pagesSona Namitha - Cost EvauationSHYAM SUNDARNo ratings yet
- Emmission and Peformance Analysis of The Ternary DDocument21 pagesEmmission and Peformance Analysis of The Ternary DSHYAM SUNDARNo ratings yet
- Yuvaraj - Guidelines For ReliabilityDocument10 pagesYuvaraj - Guidelines For ReliabilitySHYAM SUNDARNo ratings yet
- Essai Mozhi - CMTDocument30 pagesEssai Mozhi - CMTSHYAM SUNDARNo ratings yet
- Puducherry Tehnological University Newer Materials and ProcessingDocument22 pagesPuducherry Tehnological University Newer Materials and ProcessingSHYAM SUNDARNo ratings yet
- Mof Two MarksDocument17 pagesMof Two MarksSHYAM SUNDARNo ratings yet
- Emmission and Peformance Analysis of The Ternary DDocument21 pagesEmmission and Peformance Analysis of The Ternary DSHYAM SUNDARNo ratings yet
- Mechnotes: Unit Ii Kinematics of MotionDocument38 pagesMechnotes: Unit Ii Kinematics of MotionSHYAM SUNDARNo ratings yet
- Homework 1-8 Rounding On The Number LineDocument7 pagesHomework 1-8 Rounding On The Number Lineafnoawnnaeykxk100% (1)
- Assignment#2, Potential, Capacitors, Magnetic Force and FieldDocument5 pagesAssignment#2, Potential, Capacitors, Magnetic Force and FieldBilal KhalidNo ratings yet
- Spherical Harmonics: LM L L LM L LM M LM LDocument10 pagesSpherical Harmonics: LM L L LM L LM M LM LJumar CadondonNo ratings yet
- Pipe Flex Mar19Document5 pagesPipe Flex Mar19Joe Wong Wai Chuan100% (1)
- Coordination Chemistry Bonding in Transition-Metal ComplexesDocument45 pagesCoordination Chemistry Bonding in Transition-Metal ComplexessandraagustinNo ratings yet
- Be Awp MaterialDocument17 pagesBe Awp Materialsravan_4510% (1)
- Cheat Sheet: Created by Tomi MesterDocument12 pagesCheat Sheet: Created by Tomi MesterFinest Edits100% (1)
- Table of DerivativesDocument1 pageTable of DerivativesAnaKristineBalbuenaAnoba0% (1)
- 6193d861716d5 Aben 147 Laboratory Exercise No. 4 Determination of Thermal Properties of Ab Materials A Computational Laboratory ExerciDocument10 pages6193d861716d5 Aben 147 Laboratory Exercise No. 4 Determination of Thermal Properties of Ab Materials A Computational Laboratory ExerciHeliNo ratings yet
- 04302522Document6 pages04302522proteccionesNo ratings yet
- Chaptetr 1 Solution Steven M KAYDocument4 pagesChaptetr 1 Solution Steven M KAYMuhammad Usman IqbalNo ratings yet
- Ranged Queries Using Bloom Filters FinalDocument19 pagesRanged Queries Using Bloom Filters FinalAlice Qing WongNo ratings yet
- Reactor DesignDocument181 pagesReactor DesignRam0% (1)
- Condition Monitoring of Self Aligning Carrying Idler (SAI) inDocument6 pagesCondition Monitoring of Self Aligning Carrying Idler (SAI) injhon ortizNo ratings yet
- Bangladesh Informatics Olympiad 2012 (Divisional)Document5 pagesBangladesh Informatics Olympiad 2012 (Divisional)Science Olympiad BlogNo ratings yet
- Advertisement - ASI - Operator & Mechanic - 2011Document4 pagesAdvertisement - ASI - Operator & Mechanic - 2011Srikant RaoNo ratings yet
- Math 7Document20 pagesMath 7Jaysie EscalanteNo ratings yet
- Reference BookDocument1 pageReference BookAnkita Priyadarsini0% (1)
- Bomba de Lodo Gardner Denver Pz10Document2 pagesBomba de Lodo Gardner Denver Pz10Luis Alfredo Gregorio RivasNo ratings yet
- DeLanda, M. - Intensive Science and Virtual Philosophy (On Deleuze) (Continuum 2002)Document125 pagesDeLanda, M. - Intensive Science and Virtual Philosophy (On Deleuze) (Continuum 2002)Eduardo100% (5)
- CBSE Sample Paper Class 7 Maths Half Yearly Set 2Document6 pagesCBSE Sample Paper Class 7 Maths Half Yearly Set 2Prakarsh PrasadNo ratings yet
- Exact Solutions of The Ising Model in 1 and 2 Dimensions PDFDocument5 pagesExact Solutions of The Ising Model in 1 and 2 Dimensions PDFLeonardo Suárez SánchezNo ratings yet
- Manufacturing Cost EstimationDocument22 pagesManufacturing Cost EstimationJorge Sandoval JuarezNo ratings yet
- OpDocument88 pagesOpMahmud Rahman BizoyNo ratings yet
- HydrographDocument31 pagesHydrographAmer JumahNo ratings yet
- Encyclopedia of Psychology 8 Volume Set PDFDocument497 pagesEncyclopedia of Psychology 8 Volume Set PDFzahrali0% (2)
- VibbbDocument4 pagesVibbbRaj K BhattaNo ratings yet
- Gamtek Lec02 PDFDocument27 pagesGamtek Lec02 PDFagus purwadiNo ratings yet
- Cramer JohnDocument59 pagesCramer JohnClifford StoneNo ratings yet
- Unit-2 Propositional Logic and Predicate LogicDocument15 pagesUnit-2 Propositional Logic and Predicate LogicPriyank PatelNo ratings yet