Professional Documents
Culture Documents
Laplace's Equation: U U A B C Exp D Exp
Uploaded by
Sushmita ShubhamOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Laplace's Equation: U U A B C Exp D Exp
Uploaded by
Sushmita ShubhamCopyright:
Available Formats
Laplace’s equation
∇2 u = 0
If expressed in two-dimensional polar coordinates (see section 4), a solution is
! "! "
u(ρ, ϕ) = Aρn + Bρ−n C exp(inϕ) + D exp(−inϕ)
where A, B, C, D are constants and n is a real integer.
If expressed in three-dimensional polar coordinates (see section 4) a solution is
! " ! "
u(r, θ , ϕ) = Arl + Br−(l +1) Plm C sin mϕ + D cos mϕ
where l and m are integers with l ≥ |m| ≥ 0; A, B, C, D are constants;
# $| m |
d
Plm (cos θ ) = sin|m| θ Pl (cos θ )
d(cos θ )
is the associated Legendre polynomial.
Pl0 (1) = 1.
If expressed in cylindrical polar coordinates (see section 4), a solution is
! "! "
u(ρ, ϕ, z) = Jm (nρ) A cos mϕ + B sin mϕ C exp(nz) + D exp(−nz)
where m and n are integers; A, B, C, D are constants.
Spherical harmonics
The normalized solutions Ylm (θ , ϕ) of the equation
# % & $
1 ∂ ∂ 1 ∂2
sin θ + Ylm + l (l + 1)Ylm = 0
sin θ ∂θ ∂θ sin2 θ ∂ϕ2
are called spherical harmonics, and have values given by
' (
2l + 1 (l − |m|)! m m
m
Yl (θ , ϕ) = Pl (cos θ ) e imϕ
× (−1) for m ≥ 0
4π (l + |m|)! 1 for m < 0
) ) )
0 1 0 3 ±1 3
i.e., Y0 = , Y1 = cos θ, Y1 = ∓ sin θ e±iϕ , etc.
4π 4π 8π
Orthogonality
Z
Yl∗m Ylm! dΩ = δ ll ! δmm!
!
4π
12. Calculus of Variations
Z b
% &
∂F d ∂F dy
The condition for I = F ( y, y #, x) dx to have a stationary value is = # , where y =
#
. This is the
a ∂y dx ∂y dx
Euler–Lagrange equation.
17
You might also like
- Functional Operators (AM-22), Volume 2: The Geometry of Orthogonal Spaces. (AM-22)From EverandFunctional Operators (AM-22), Volume 2: The Geometry of Orthogonal Spaces. (AM-22)No ratings yet
- Galois Theory: Prof. A.J. Scholl Michaelmas 2005Document65 pagesGalois Theory: Prof. A.J. Scholl Michaelmas 2005Abed AbedelfatahNo ratings yet
- Calculus Cheat Sheet Part 3Document4 pagesCalculus Cheat Sheet Part 3Dave Cloud100% (12)
- Homework #7, Sec 12.2Document6 pagesHomework #7, Sec 12.2Masaya SatoNo ratings yet
- DLL 1st Week For Math 8Document6 pagesDLL 1st Week For Math 8Melba RamosNo ratings yet
- Classical Number Theory - Reid Barton - MOP (Black) 2004Document4 pagesClassical Number Theory - Reid Barton - MOP (Black) 2004Alexandru PîrvuceanuNo ratings yet
- Iyanaga S. - Algebraic Number TheoryDocument155 pagesIyanaga S. - Algebraic Number TheoryJohnnyNo ratings yet
- HW 12-14Document1 pageHW 12-14lolnationNo ratings yet
- 240 BnotesDocument112 pages240 BnotesJose Luis GiriNo ratings yet
- Raich Lecture2Document109 pagesRaich Lecture2Rodrigo MendesNo ratings yet
- DueDocument38 pagesDuecaiooo3No ratings yet
- SphericalHarmonics 12 PDFDocument14 pagesSphericalHarmonics 12 PDFMateo TopalovićNo ratings yet
- Nevannlina Theory and Some Related ProblemsDocument8 pagesNevannlina Theory and Some Related ProblemsPrevalisNo ratings yet
- Legendre & Spherical HarmonicsDocument15 pagesLegendre & Spherical HarmonicsCal FfbdsfsgNo ratings yet
- Lindemann-Weierstrass TheoremDocument6 pagesLindemann-Weierstrass TheoremAndrés GranadosNo ratings yet
- Example:: CSC418 / CSCD18 / CSC2504 CurvesDocument5 pagesExample:: CSC418 / CSCD18 / CSC2504 CurvesMuhammedNo ratings yet
- λ and vectors x = 0 f or which Ax = λxDocument22 pagesλ and vectors x = 0 f or which Ax = λxJohn MarkNo ratings yet
- Linear PdeDocument23 pagesLinear PdeA SinghNo ratings yet
- Laplace'S and Poisson'S EquationsDocument16 pagesLaplace'S and Poisson'S EquationsOBStaffNo ratings yet
- Mid400 19Document2 pagesMid400 19I Gede ArjanaNo ratings yet
- Summary of Angular Momentum: X Z y y X Z Z y XDocument3 pagesSummary of Angular Momentum: X Z y y X Z Z y XEugenio CapielloNo ratings yet
- Higgs Bundles CIEM 200802Document35 pagesHiggs Bundles CIEM 200802Ismail KhanNo ratings yet
- Matrix Airy Functions For Compact Lie Groups: V. S. Varadarajan University of California, Los Angeles, CA, USADocument17 pagesMatrix Airy Functions For Compact Lie Groups: V. S. Varadarajan University of California, Los Angeles, CA, USAhelmantico1970No ratings yet
- Prime PDFDocument43 pagesPrime PDFKhokon GayenNo ratings yet
- 18.034 Honors Differential Equations: Mit OpencoursewareDocument4 pages18.034 Honors Differential Equations: Mit OpencoursewareTanzina ArpaNo ratings yet
- Garrett P. - Simple Proof of The Prime Number TheoremDocument9 pagesGarrett P. - Simple Proof of The Prime Number TheoremcleobuloNo ratings yet
- Partial Differentiation (Book Chapters From Bird's Higher Engineering Mathematics)Document24 pagesPartial Differentiation (Book Chapters From Bird's Higher Engineering Mathematics)i21020652No ratings yet
- Chapter Three: 3.2 Legendre Equation and Legendre PolynomialsDocument73 pagesChapter Three: 3.2 Legendre Equation and Legendre PolynomialsPatrick SibandaNo ratings yet
- Qfti Homework 1 Solution: 1.1 ProblemDocument9 pagesQfti Homework 1 Solution: 1.1 ProblemshaniNo ratings yet
- The Lefschetz Fixed Point Theorem: Frederik VercauterenDocument26 pagesThe Lefschetz Fixed Point Theorem: Frederik VercauterendmtriNo ratings yet
- Mit8 323 s23 Pset01Document6 pagesMit8 323 s23 Pset01Ayham ziadNo ratings yet
- SteedDocument5 pagesSteedAlbertoAlcaláNo ratings yet
- Final 07Document4 pagesFinal 07Sutirtha SenguptaNo ratings yet
- Proof of The Lagrange Inversion FormulaDocument4 pagesProof of The Lagrange Inversion FormulaVictor MarchantNo ratings yet
- Relativistic Quantum Mechanics: Exercises: Preprint Typeset in JHEP Style - HYPER VERSIONDocument6 pagesRelativistic Quantum Mechanics: Exercises: Preprint Typeset in JHEP Style - HYPER VERSIONMahendra SankhuaNo ratings yet
- P182 List of EquationsDocument4 pagesP182 List of EquationsRomesor ApolNo ratings yet
- Paper 48Document5 pagesPaper 48KaustubhNo ratings yet
- Entire and Meromorphic FunctionsDocument88 pagesEntire and Meromorphic FunctionsPrevalisNo ratings yet
- Stat 581 Midterm Exam Solutions (Autumn 2011)Document3 pagesStat 581 Midterm Exam Solutions (Autumn 2011)Robinson Ortega MezaNo ratings yet
- Part III Lecture Notes On The Standard Model: by H. OsbornDocument118 pagesPart III Lecture Notes On The Standard Model: by H. OsbornCharlie HultgreenNo ratings yet
- Linear SystemsDocument5 pagesLinear SystemsVedant GavhaneNo ratings yet
- Comm AlgDocument87 pagesComm AlgtolesadekebaNo ratings yet
- Integrability in Theoretical Abstract Algebra: O. O. Sun, E. Galois, E. Deligne and R. F. BhabhaDocument10 pagesIntegrability in Theoretical Abstract Algebra: O. O. Sun, E. Galois, E. Deligne and R. F. Bhabhav3rgilaNo ratings yet
- Outline Term1 4Document2 pagesOutline Term1 4Joy LahierieNo ratings yet
- Notes On Sturm-Liouville Differential Equations: 1 Recalling The Wave EquationDocument12 pagesNotes On Sturm-Liouville Differential Equations: 1 Recalling The Wave EquationSarthak VijayNo ratings yet
- LCT 4Document30 pagesLCT 4Sandipan SahaNo ratings yet
- Exam ED Aug SolDocument13 pagesExam ED Aug SolAna SultanNo ratings yet
- Physics 506: Problem Set 5: Due: October 13, 2014Document3 pagesPhysics 506: Problem Set 5: Due: October 13, 2014Ravi RoyNo ratings yet
- Unit5 DiagDocument36 pagesUnit5 DiagNaiara Fernández FernándezNo ratings yet
- Pde Slides2Document14 pagesPde Slides2ranya.baevaNo ratings yet
- Eaxm 1 NotesDocument2 pagesEaxm 1 NotesluquedonascimentoNo ratings yet
- PHYS541 Notes8Document8 pagesPHYS541 Notes8dinamitaNo ratings yet
- STD Alg3 2022-2023 N5Document3 pagesSTD Alg3 2022-2023 N5oussama.zeroualNo ratings yet
- CEE471 HW6 SolDocument7 pagesCEE471 HW6 SolJonathanNo ratings yet
- Advanced Fuzzy Dynamics: Lomani Tamanix, N. Watanabe, P. Maruyama and S. CardanoDocument10 pagesAdvanced Fuzzy Dynamics: Lomani Tamanix, N. Watanabe, P. Maruyama and S. CardanoThien ThaiNo ratings yet
- Recurrence and ErgodicityDocument19 pagesRecurrence and ErgodicityBratnokNo ratings yet
- LMMDocument10 pagesLMMSaad KhalisNo ratings yet
- Statistics 580 Maximum Likelihood Estimation: 1 2 N 0 N 1 P 0 PDocument25 pagesStatistics 580 Maximum Likelihood Estimation: 1 2 N 0 N 1 P 0 PTawsif HasanNo ratings yet
- Membranska Teorija Rotacionih Ljuski Pri Rotaciono Simetričnom OpterećenjeDocument5 pagesMembranska Teorija Rotacionih Ljuski Pri Rotaciono Simetričnom OpterećenjeLazić MilošNo ratings yet
- Definition 1.1. Suppose FDocument5 pagesDefinition 1.1. Suppose FluoNo ratings yet
- Mathgen 1009634653Document7 pagesMathgen 1009634653IvanAnusicNo ratings yet
- Lie DerivativeDocument13 pagesLie DerivativeMarco André Ferreira DiasNo ratings yet
- Fourier Series ExplainedDocument1 pageFourier Series ExplainedSushmita ShubhamNo ratings yet
- Ionic EquilibriumDocument1 pageIonic EquilibriumSushmita ShubhamNo ratings yet
- FermentDocument1 pageFermentSushmita ShubhamNo ratings yet
- Inorganic Chemistry: Periodic Table & PeriodicityDocument1 pageInorganic Chemistry: Periodic Table & PeriodicitySushmita ShubhamNo ratings yet
- Series: Arithmetic and Geometric ProgressionsDocument1 pageSeries: Arithmetic and Geometric ProgressionsSushmita ShubhamNo ratings yet
- Msths BasicsDocument1 pageMsths BasicsSushmita ShubhamNo ratings yet
- Integer Series: N N N N N N N NDocument1 pageInteger Series: N N N N N N N NSushmita ShubhamNo ratings yet
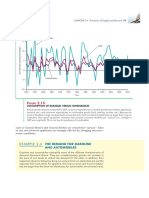
- Example 2.6: The Demand For Gasoline and AutomobilesDocument1 pageExample 2.6: The Demand For Gasoline and AutomobilesSushmita ShubhamNo ratings yet
- ElasticityDocument1 pageElasticitySushmita ShubhamNo ratings yet
- Indifference Curves: Curves. Vide A Consumer With The Same Level of Satisfaction. EntDocument1 pageIndifference Curves: Curves. Vide A Consumer With The Same Level of Satisfaction. EntSushmita ShubhamNo ratings yet
- 85 Price Changes: Consumer BehaviorDocument1 page85 Price Changes: Consumer BehaviorSushmita ShubhamNo ratings yet
- Homework Set 1: Due August 14Document3 pagesHomework Set 1: Due August 14jog10No ratings yet
- Ifp Bhss Maths Eoy Exam - Sept 12Document10 pagesIfp Bhss Maths Eoy Exam - Sept 12Yousif Mousa AdamNo ratings yet
- Bow Mathematics 7-10...Document37 pagesBow Mathematics 7-10...era resusNo ratings yet
- It Is Conceivably The Most Basic Pattern in Nature.: Regularity Movement Rhythm SymmetryDocument26 pagesIt Is Conceivably The Most Basic Pattern in Nature.: Regularity Movement Rhythm SymmetryArt lalaNo ratings yet
- (For XI & XII Studying Students) : Code-A 20/09/2021Document5 pages(For XI & XII Studying Students) : Code-A 20/09/2021HIMANI CHUNDURUNo ratings yet
- Pre-Calculus: Quarter 1 - Module 1Document22 pagesPre-Calculus: Quarter 1 - Module 1ValerieNo ratings yet
- Emcf 18 F14Document5 pagesEmcf 18 F14ShitPre SuperNo ratings yet
- Sample Paper 3Document15 pagesSample Paper 3SahanaaNo ratings yet
- CosineDocument10 pagesCosineSohaib AslamNo ratings yet
- Mathematics of Cryptography: Part I: Modular Arithmetic, Congruence, and MatricesDocument78 pagesMathematics of Cryptography: Part I: Modular Arithmetic, Congruence, and MatricesGauravGargNo ratings yet
- DRM SolutionsDocument116 pagesDRM SolutionsCésar TapiaNo ratings yet
- Math Review For Practicing To Take The GRE General TestDocument69 pagesMath Review For Practicing To Take The GRE General TestMd.Mahbubul BasharNo ratings yet
- Relativity EssayDocument15 pagesRelativity EssayQuinto BeatleNo ratings yet
- Proof of The Orthogonality RelationsDocument3 pagesProof of The Orthogonality RelationsDeepikaNo ratings yet
- Quiz 2Document6 pagesQuiz 2dharmendra_kanthariaNo ratings yet
- ch02 PDFDocument108 pagesch02 PDFtoligado27No ratings yet
- Basic Algebra Bridge CourseDocument24 pagesBasic Algebra Bridge CourseongcristoffNo ratings yet
- Solving Cubic Equations Roots Trough Cardano TartagliaDocument2 pagesSolving Cubic Equations Roots Trough Cardano TartagliaClóvis Guerim VieiraNo ratings yet
- Differential Calculus - DPP - 02 PDFDocument8 pagesDifferential Calculus - DPP - 02 PDFashrithNo ratings yet
- Tugas MatematikaDocument46 pagesTugas MatematikaHasan HairullaNo ratings yet
- Hitchin-2001-Stable Forms and SpecialDocument31 pagesHitchin-2001-Stable Forms and SpecialGuido FranchettiNo ratings yet
- 9.3 Notes-AnswersDocument5 pages9.3 Notes-AnswersFausto SosaNo ratings yet
- June 2014 (R) MS - C4 EdexcelDocument24 pagesJune 2014 (R) MS - C4 EdexcelMomen YasserNo ratings yet
- Y Sec 2t Sec 2t: What Is The Value of The Derivative of The Function Below For T 1? The Given Angle Is in RadiansDocument24 pagesY Sec 2t Sec 2t: What Is The Value of The Derivative of The Function Below For T 1? The Given Angle Is in RadiansRhian LlerinNo ratings yet
- The Jesuit Mathletes PacketDocument24 pagesThe Jesuit Mathletes PacketChris EurNo ratings yet
- Fundamental Concepts of Triangles: Sides of A TriangleDocument13 pagesFundamental Concepts of Triangles: Sides of A TriangleRajni KashyapNo ratings yet
- CCS 1501-Engineering Mathematics Unit 1 Introductory Theory of SetsDocument26 pagesCCS 1501-Engineering Mathematics Unit 1 Introductory Theory of SetsMapalo zimbaNo ratings yet
- Chapter 2 Deterministic and Random Signal AnalysisDocument106 pagesChapter 2 Deterministic and Random Signal AnalysisgrasspackingNo ratings yet