A B C D E F G H I J K

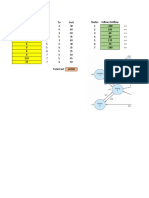
1 RedBrand shipping model

2
3 Inputs
4 Common arc capacity 200
5
6 Network structure, flows, and arc capacity constraints Node balance constraints
7 Origin Destination Unit Cost Flow Arc Capacity Plant constraints
8 1 2 5 0 <= 200 Node Plant net outflow Plant capacity
9 1 3 3 180 <= 200 1 180 <= 200
10 1 4 5 0 <= 200 2 300 <= 300
11 1 5 5 0 <= 200 3 100 <= 100
12 1 6 20 0 <= 200
13 1 7 20 0 <= 200 Warehouse constraints
14 2 1 9 0 <= 200 Node Warehouse net outflow Required
15 2 3 9 0 <= 200 4 0 = 0
16 2 4 1 120 <= 200 5 0 = 0
17 2 5 1 0 <= 200
18 2 6 8 180 <= 200 Customer constraints
19 2 7 15 0 <= 200 Node Customer net inflow Customer demand
20 3 1 0.4 0 <= 200 6 400 >= 400
21 3 2 8 0 <= 200 7 180 >= 180
22 3 4 1 80 <= 200
23 3 5 0.5 200 <= 200 Range names used
24 3 6 10 0 <= 200 Arc_Capacity =Model!$F$8:$F$33
25 3 7 12 0 <= 200 Customer_demand =Model!$K$20:$K$21
26 4 5 1.2 0 <= 200 Customer_net_inflow =Model!$I$20:$I$21
27 4 6 2 200 <= 200 Destination =Model!$B$8:$B$33
28 4 7 12 0 <= 200 Flow =Model!$D$8:$D$33
29 5 4 0.8 0 <= 200 Origin =Model!$A$8:$A$33
30 5 6 2 200 <= 200 Plant_capacity =Model!$K$9:$K$11
31 5 7 12 0 <= 200 Plant_net_outflow =Model!$I$9:$I$11
32 6 7 1 180 <= 200 Total_cost =Model!$B$36
33 7 6 7 0 <= 200 Unit_Cost =Model!$C$8:$C$33
34 Warehouse_net_outflow =Model!$I$15:$I$16
35 Objective to minimize
36 Total cost $3,260 Because of computer roundoff, it is possible that This network model is much more general than the basic transportation model.
an arc at capacity might not be exactly at Here are differences: (1) goods can flow into or out of any of the nodes; (2) some
capacity. Its flow might be something like nodes are net suppliers (although arcs can flow into them), others are net
199.99999. Therefore, to be safe, the formula in demanders (although arcs can lead out of them), and the rest are "transshipment"
cell B39 could be changed to something like nodes, where no goods originate or end up; (3) many potential arcs can be missing,
=COUNTIF(Flow,">"&B4-0.00001). This checks so that we include only the allowable arcs in the list in columns A-D; and (4) arcs can
for flows that are essentially at capacity except (but don't have to) have arc capacities. Actually, some or all arcs can have nonzero
for roundoff. lower bounds, and this doesn't make the model any more difficult to model or solve.
As with the basic transportation and assignment models, if the capacities and
demands are integers and there are no side constraints, the optimal solution is
guaranteed to have integers for the changing cells -- without imposing integer
constraints. This is extremely important. Logistics models in the real world are
typically huge, and they would be much more difficult to solve, maybe even
impossible, if we had to impose integer constraints.
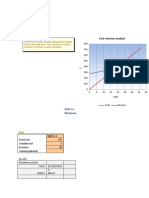
Oneway analysis for Solver model in Model worksheet

Common arc capacity (cell $B$4) values along side, output cell(s) along top

Arcs_at_capacity
Total_cost

1
150 $4,120 5
175 $3,643 6
200 $3,260 3
225 $2,998 3
250 $2,735 3
275 $2,473 3
300 $2,320 2

It is pretty clear that as the common arc

capacity increases, the optimal total
Se
cost decreases, as shown in the chart. 4500
The number of flows equal to the arc
capacity also decreases. 4000
3500
3000
2500
2000
1500
1000
500
0
150
Sensitivity of Total_cost to Common arc capacity

Data for chart

When you select an output from the
dropdown list in cell $K$4, the chart
will adapt to that output.
Total_cost

4120
3642.5
3260
2997.5
2735
2472.5
2320

Sensitivity of Total_cost to Common arc capacity

4500
4000
3500
3000
2500
2000
1500
1000
500
0
150 175 200 225 250 275 300
Common arc capacity ($B$4)