Fundamentals 13

F(xα)
F(x) 0.5

0
0 50 100 xα150 200
x

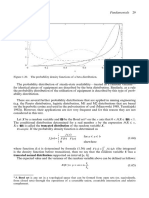
Figure 1.4. Quantile of the order α in the distribution F(x).

data13 and is independent of any distance metric. In a sample of data or a finite population,
there may be no member of the sample whose value is identical to the median (in the case of
an even sample size), and, if there is such a member, there may be more than one so that the
median may not uniquely identify a sample member.
The medians of certain types of distributions can be easily calculated from their parameters,
e.g. the median of a Cauchy’s distribution with the location parameter x0 and the scale parameter y
is x0, the location parameter. But for some distributions median formulas are complicated or there
is no single formula that can be used to find the median (for example, Binomial distribution).

The mode of a random variable X (Mo(X)) is such that its value corresponds with:
− the greatest probability of the occurrence when the random variable is a discrete one
− the local maximum of the probability density function when the random variable is a con-
tinuous one.
Like the mean and median, the mode is a way of expressing, in a single number, important
information about a random variable or a population. The mode is not necessarily unique,
since the same maximum frequency may be attained at different values. The most extreme
case appears in uniform distribution, where all values occur equally frequently.
Information on the mode (sometimes called a dominant) of a given random variable is
important when the prognosis of realisation of this random variable should be done and
this prognosis will be done only once (not repeated). The proposed value should be simply
the mode because it has the greatest chances of occurring. This prognosis can be different if
additional information is at hand.

Of particular value are order statistics and their functions, which are used to estimate
order parameters.
Let X1, X2, …, Xn be an n-dimensional random vector and let x1, x2, …, xn be its realisa-
tion. The order statistic Xk,n is a function of the random variables X1, X2, …, Xn taking the
k-th largest value in each sequence of values x1, x2, …, xn. Order statistics are important, for
instance, in durability studies.

1.2.4 Relationships between parameters of random variables

When the probability distribution of a random variable is a symmetric one, then its expected
value, its mode and its median take the same value14, e.g. for the Gaussian distribution. In a
case where a given distribution is asymmetric, these basic parameters of the random variable
are different in value. A moderately asymmetric probability density function having a positive
skew and positions of the mean, median and mode are shown in Figure 1.5.

13
A geometric median, on the other hand, is defined in any number of dimensions.
14
Some exceptions such as the Cauchy’s distribution or the uniform one, for instance, are neglected here.

Book.indb 13 12/9/2013 12:22:03 PM