RANDOM VARIABLES AND DISTRIBUTIONS

Review Isaiah
Binomial problems: Advanced

Español

Explanation Page
QUESTION

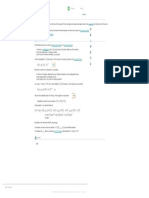
Suppose that 55% of all babies born in a particular hospital are girls. If 7 babies born in the hospital are randomly selected, what is the probability that at most
2 of them are girls?
Carry your intermediate computations to at least four decimal places, and round your answer to two decimal places.

(If necessary, consult a list of formulas.)

EXPLANATION

If the following are true, we have a binomial experiment (or a binomial situation).

There are n independent trials. (The occurrence of one doesn't affect any of the others.)
Each trial ends either in success or failure.
Each trial has the same probability p of success.

Then the probability P x that exactly x of the trials end in success is given by the binomial formula.
x n−x
P x = nCx·p 1 − p More

Note that we have such a situation in our problem.

There are 7 babies. Because they are randomly selected, we have independent trials.
Each baby either is a girl or isn't.
Each baby has a 55% chance of being a girl.

So, using n = 7 and p = 0.55, here is the probability P x that exactly x of the babies are girls.
x 7−x
P x = 7Cx· 0.55 1 − 0.55     (1)

We want the probability that at most 2 of the babies are girls. More

Probability at most 2 are girls = P 0 + P 1 + P 2

Using equation 1, we get the following.

0 7 1 6 2 5
P 0 + P 1 + P 2 = 7C0· 0.55 1 − 0.55 + 7C1· 0.55 1 − 0.55 + 7C2· 0.55 1 − 0.55
0 7 1 6 2 5
= 1· 0.55 0.45 + 7· 0.55 0.45 + 21· 0.55 0.45
  ≈ 0.1529

Rounding to the nearest hundredth, we get 0.15.

The answer can also be found by inputting P B7 ,  0.55   ≤ 2 on the ALEKS calculator.

The notation B7 ,  0.55 refers to a binomial random variable with parameters n = 7 and p = 0.55.

ANSWER

0.15

More Practice

© 2022 McGraw Hill LLC. All Rights Reserved. Terms of Use | Privacy Center | Accessibility