RANDOM VARIABLES AND DISTRIBUTIONS

Review Isaiah
Binomial problems: Advanced

Español

Explanation Page
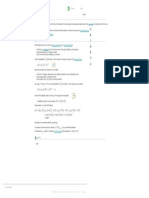
QUESTION

10 questions. Each question has answer choices of a, b, c, d, and e, and only one of the choices is correct. If a student
A multiple-choice test consists of
randomly guesses on each question, what is the probability that she gets fewer than 2 of them correct?

Carry your intermediate computations to at least four decimal places, and round your answer to two decimal places.

(If necessary, consult a list of formulas.)

EXPLANATION

If the following are true, we have a binomial experiment (or a binomial situation).

There are n independent trials. (The occurrence of one doesn't affect any of the others.)
Each trial ends either in success or failure.
Each trial has the same probability p of success.

Then the probability P x that exactly x of the trials end in success is given by the binomial formula.
x n−x
P x = nCx·p 1 − p More

Note that we have such a situation in our problem.

There are 10 questions. Because the student is randomly guessing, we have independent trials.
Each question either is answered correctly or isn't.
1
Each question has a probability of being answered correctly (because each question has 5 answer choices and the student is randomly guessing).
5

1
So, using n = 10 and p = , here is the probability P x that the student gets exactly x questions correct.
5
x 10 − x
1 1
P x = 10Cx· 1−     (1)
5 5

We want the probability that the student gets fewer than 2 of the questions correct. More

Probability gets fewer than 2 correct = P 0 + P 1

Using equation 1, we get the following.

0 10 1 9
P 0 +P 1 = C · 1 1−
1
+ 10C1·
1
1−
1
10 0 5 5 5 5
0 1
1 10 1 9
= 1· 0.8 + 10· 0.8
5 5
  ≈ 0.3758

Rounding to the nearest hundredth, we get 0.38.

The answer can also be found by inputting P B 1  ≤1 on the ALEKS calculator.
10 , 
5
1
The notation B 1 refers to a binomial random variable with parameters n = 10 and p = .
10 ,  5
5

ANSWER

0.38

More Practice

© 2022 McGraw Hill LLC. All Rights Reserved. Terms of Use | Privacy Center | Accessibility