F INAL

M ATH 2210
Fall 2021

Name (Printed) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Name (Signature) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Coyote ID . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Section Number . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Instructor Name . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Instructions:
• -5 points for not legibly filling out the box with the name and student id #.
• This exam has 7 problems and 100 points. Check all pages are included.
• Read each problem carefully and write legibly.
• Show ALL your work to receive credit! Cross off anything you do not wish graded.
• No credit will be given for answers with no work shown, unless noted in problem.
• You may use one personal (not shared) 3x5 inch notecard of notes, a scientific or graphing
calculator, and a writing utensil.
• You may NOT use anything else (e.g. books, notes, phones, watches, earbuds, or head-
phones).
• Problems are of varying difficulty. Be sure to pace yourself and move on from a question
if you are stuck - you can return to it later.
• You have 110 minutes to complete this exam.

F ILL OUT AFTER COMPLETING EXAM

Question: 1 2 3 4 5 6 7 Total
Time when
Points: 20 10 15 15 10 15 15 100 completed: . . . . . . . . . . . . . . . . . . . . . . . . . . . .

© Copyright: California State University, San Bernardino, 2021.

 Question 1 (20 points) For each of the following, circle the correct answer. 2 points each. No partial credit
and no credit if more than one answer on a question is selected.
(1). Suppose that f (x) is a differentiable function and you know that f (7) = 3.6 and f 0 (7) = 0.1. What
is the most appropriate statement?
(A). The value of f (8) is 3.7.
(B). With each increase one unit of input, the output increases by 0.1
(C). The value of f (8) is approximately 0.1.
(D). The value of f (8) is approximately 3.7.
(E). With each increase 7 units of input, the output increases by approximately 0.1
(F). None of the above.

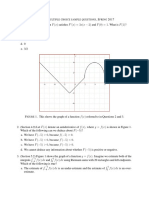
(2). Suppose that h(x) is a differentiable function and to the right is

5 y
a graph of h 0 (x) on the domain [−3, 2]. At approximately which
point listed below does h(x) have a local maximum? 4

3
(A). x ≈ −3
2
(B). x ≈ −2.3
1
(C). x ≈ −1.3
x
(D). x ≈ 0.2 −3 −2 −1 1 2
−1
(E). x ≈ 0.8
−2
(F). None of the above
−3

(3). Two cars start at the same time and travel in the same direction along a straight road. The figure
below gives the velocity, v, of each car as a function of time, t . Which of the following statements
best describe the movement of the cars?

(A). Car B attains a larger maximum velocity, but Car A travels farther.

(B). Car A attains a larger maximum velocity, but Car B travels farther.

(C). Car A attains a larger maximum velocity and Car A travels farther.

(D). Car B attains a larger maximum velocity and Car B travels farther.

(E). Car A attains a larger maximum velocity, but they travel the same distance.

(F). None of the above.

© Copyright: California State University, San Bernardino, 2021. Page 2 of 10

 (4). Suppose that g (x) is a differentiable function and g 0 (x) = e −x (x + 2)(x − 3). Which of the following
must be true?
(A). g (x) has critical points at x = 0, −2, 3.
(B). g (x) has a global minimum at x = 3.
(C). g (x) has a local minimum at x = 3.
(D). g (x) has a local maximum at x = 3.
(E). g (x) has a global maximum at x = 3.
(F). None of the above.

(5). Given the below table of values of the differentiable function f (x), which is the most appropriate
statement regarding f 0 (2)?
(A). f 0 (2) is exactly 18.

(B). f 0 (2) is approximately 18.

(C). f 0 (2) is approximately 3.5.

x 0 2 4 6
0
(D). f (2) is exactly 8. f (x) 10 18 24 21
(E). f 0 (2) is approximately 8.

(F). f 0 (2) is exactly 4.

(6). Given the below table of values of the derivative function H 0 (x) of a differentiable function H (x).
What is the most appropriate about the concavity of H (x) at x = 3?

(A). It is concave up because H 0 (x) is increasing at x = 3.

(B). It is concave down because H 0 (3) is negative.

(C). It is concave up because H 0 (x) is negative.

x 1 2 3 4
0
(D). It is concave down because H (x) is increasing at x = 3. H 0 (x) −9 −5 −1 2
(E). It is concave down because H 0 (x) is decreasing in magnitude at x = 3.

(F). It is concave up because H 0 (x) is decreasing in magnitude at x = 3.

© Copyright: California State University, San Bernardino, 2021. Page 3 of 10

 (7). For this and the next question, use the following graphs of the functions f (x) and g (x).

80 80

60 60

40 f (x) 40 g (x)
20 20
x x
20 40 60 80 20 40 60 80

If h(x) = f (g (x)), what is h 0 (20)?

1
(A). 20 (B). 5 (C). 2 (D). 1 (E). −2 (F). 0

(8). Use the above graphs of the functions f (x) and g (x). If j (x) = f (x)g (x), what is j 0 (60)?
1
(A). 20 (B). 30 (C). 2 (D). 0 (E). 1 (F). 60

(9). Suppose that S(x) = sinx x . Which of the following is the most appropriate statement at x = 0?
(A). S(0) = 0.
(B). limx→0 S(x) = 1 but S(x) is not defined at x = 0.
(C). limx→0 S(x) = 1 and S(0) = 1.
(D). limx→0 S(x) = ∞ and S(x) is not defined at x = 0.
(E). S(x) is continuous at x = 0.
(F). None of the above are true.

(10). Suppose that k(x) is a continuous function defined

5 y
on the domain 0 ≤ x ≤ 5 and is graphed to the right.
What collection is the complete list of critical points
of k(x)? 4

(A). x = 1, 4
3
(B). x = 2, 3

(C). x = 0, 5 2 k(x)
(D). x = 1, 2, 3, 4
1
(E). x = 0, 1, 2, 3, 4, 5
x
(F). None of the above are correct
1 2 3 4 5

© Copyright: California State University, San Bernardino, 2021. Page 4 of 10

Question 2 (10 points) The graph of f (t ) below gives the position of a particle at time t .

Consider the following quantities:

3 f (t ) • A, average velocity between t = 1 and t = 3,

• B , average velocity between t = 5 and t = 6,

• C , instantaneous velocity at t = 1,
2
• D, instantaneous velocity at t = 3,

• E , instantaneous velocity at t = 5,
1
• F , instantaneous velocity at t = 6.

t
1 2 3 4 5 6
Arrange the above 6 quantities from least to greatest.

< < < < <

Clearly explain your reasoning below.

© Copyright: California State University, San Bernardino, 2021. Page 5 of 10

Question 3 (15 points) Compute the derivatives of each of the following functions. Be sure to clearly state
the name of a differentiation rule each time you use it.
(a). (5 points) f (x) = e x sin(x)

(b). (5 points) g (x) = cos7 (x)

2x+1
(c). (5 points) h(x) = 6x+5

© Copyright: California State University, San Bernardino, 2021. Page 6 of 10

 Question 4 (15 points) Census figures for the US population (in millions) are listed in the table below. Let
f be the function such that P = f (t ) is the population (in millions) at year t .

Year 1950 1960 1970 1980 1990

Population 150.7 179.0 205.0 226.5 248.7

Assume that f is increasing, so f is invertible.

(a). (3 points) What is the meaning of f (1980)?

(b). (4 points) What does the derivative of f (Y ) at Y = 1980 represent? What are its units? Your re-
sponse should be a clear, complete sentence.

(c). (3 points) What is the meaning of f −1 (200)?

Since f determines the population size P in millions at year t, f-inverse will determine the year at which the
population size is P. So f-inverse of 200 means the year at which the population size is 200 million.

(d). (4 points) What does the derivative of f −1 (P ) at P = 200 represent? What are its units? Your
response should be a clear, complete sentence.

When the population is 200 million, f-inverse of 200 determines the year t at which the population will increase by 1 million

(e). (1 point) Estimate f −1 (200).

© Copyright: California State University, San Bernardino, 2021. Page 7 of 10

Question 5 (10 points) A potter forms a piece of clay into a cylinder. As she rolls it, the length, L, of the
cylinder increases and the radius, r , decreases. If the length of the cylinder is increasing at 0.1 cm/sec,
find the rate at which the radius in changing when the radius is 1 cm and the length is 5 cm. (Note: A
cylinder with radius r and length L has volume V = πr 2 L.)

© Copyright: California State University, San Bernardino, 2021. Page 8 of 10

Question 6 (15 points) In order to survive and perform their tasks, cells in your body must simultane-
ously produce and break down a molecule called ATP. When ATP is broken down, energy is released
to the cell, and ATP is destroyed. For a certain cell, the rate of production of ATP, P (t ), in millions of
molecules per second, and the rate at which ATP is broken down, C (t ), also in millions of molecules
per second, are given in the following figure, where t is in seconds. The graph of P (t ) is shown as a
solid line, and C (t ) is dashed.

(a). (5 points) At time t = 1, is ATP increasing or decreasing? Be sure to clearly justify your conclusion
using data from the above graph. No points if there is no justification.

(b). (5 points) At approximately what time between t = 0 and t = 6 does the cell have the greatest
amount of ATP? Be sure to clearly justify your conclusion using data from the above graph. No
points if there is no justification.

(c). (5 points) At approximately what time between t = 0 and t = 6 is the amount of ATP in the cell
decreasing the fastest? Be sure to clearly justify your conclusion using data from the above graph.
No points if there is no justification.

© Copyright: California State University, San Bernardino, 2021. Page 9 of 10

Question 7 (15 points) A local garden store plans to build
a large rectangular sign on the interior wall at one
end of their greenhouse. The roof along this wall is
centered around a vertical support beam. The height
of the roof, r (measured in meters), can be expressed
as a function the horizontal distance from the verti-
cal support beam, x (measured in meters), by

5 2
r (x) = 5 − x − 4 ≤ x ≤ 4.
16
This curve is graphed to the right; the shaded rect-
angle is one possible sign that could be built.

The store wants to create the largest sign it can. x

−4 4
(a). (5 points) Write the area A(x) of the sign (in square meters), as a function of x, Be sure to specify
the domain of A(x).

(b). (10 points) Find the value(s) of x for which the sign has the largest possible area. Use calculus
to find your answers, and be sure to show enough evidence that the values you find do in fact
maximize the area.

© Copyright: California State University, San Bernardino, 2021. Page 10 of 10